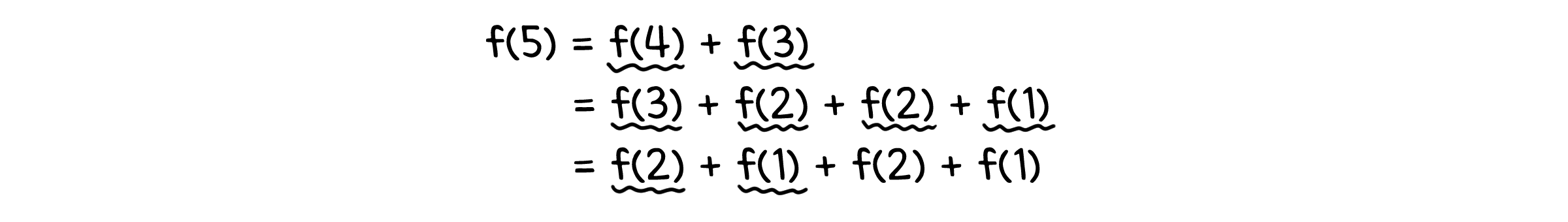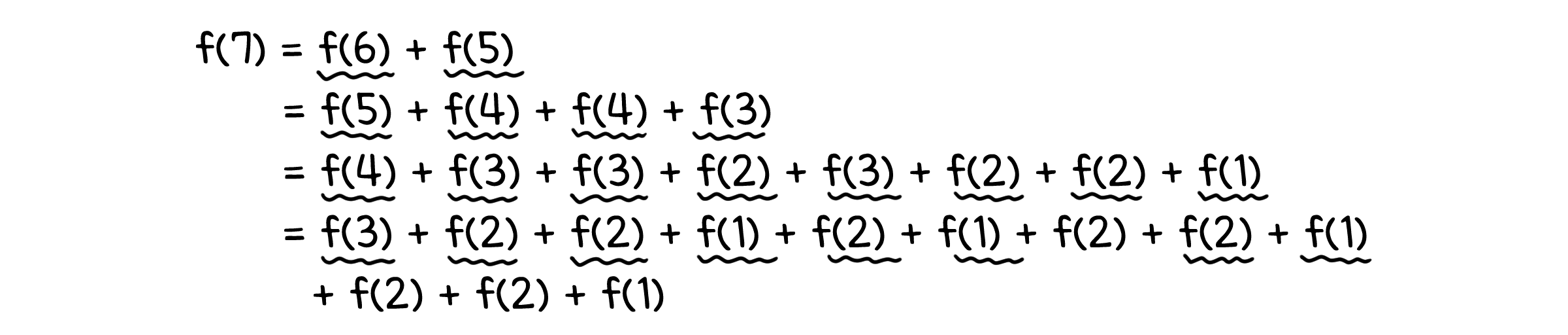[CM301] 09. 동적 계획법 I (Dynamic Programming I)

게시 2026/01/12 업데이트 2026/01/13

15 분정도 걸립니다

[CM301] 09. 동적 계획법 I (Dynamic Programming I)

알고리즘

탐욕적 알고리즘은 부분 문제가 최적일 때 전체 문제도 최적이 된다는 전략으로, 빠르게 답을 도출할 수 있지만 항상 최적의 답을 도출하는 것은 아니라는 문제가 있었습니다.

이번에는 탐욕적 알고리즘만큼 빠르지는 않지만, 확실하게 답을 찾을 수 있는 디자인 패러다임인 동적 계획법(Dynamic Programming)과 이를 활용한 문제들에 대해 살펴보겠습니다.

동적 계획법 (Dynamic Programming)

동적 계획법은 주어진 문제를 더 작은 문제들로 이루어진 것으로 생각하여 해결하는 철학의 패러다임입니다. 작은 문제를 먼저 해결하고, 그 다음 더 큰 문제를 해결하는데 작은 문제의 해답을 사용하는 것이죠.

큰 문제를 작은 문제들로 나누어 해결한다는 점은 분할 정복 방식과 유사한 부분입니다. 단, 동적 계획법은 그렇게 발생한 작은 문제들이 최대한 자주 등장하도록 설계하는데 중점을 둡니다. 그 작은 문제의 답을 한 번만 계산해두면, 이후에 최대한 많이 호출하여 사용할 수 있기 때분입니다.

피보나치 수열을 예시로 들어봅시다. 피보나치 수열은 자신의 바로 이전 두 항의 합을 값으로 가지는 수열입니다.

\[f(1) = 1, f(2) = 1\] \[f(n) = f(n-1) + f(n-2)\]

식에서 대놓고 나와 있듯이, 재귀를 통해 어렵지 않게 구현할 수 있는 함수입니다.

  
def Fibonacci(n):
  if n <= 2:
    return 1
  else:
    return Fibonacci(n-1) + Fibonacci(n-2)

$n=5$인 경우를 생각해봅시다. $f(5) = f(4) + f(3), f(4) = f(3) + f(2), f(3) = f(2) + f(1)$ 이므로 $f(5)$를 계산하는 과정에서 함수는 총 여덟 번 호출됩니다.

그런데, 이 호출 횟수는 입력값이 커질수록 점점 많아지게 됩니다. $n=7$만 해도, 호출 횟수는 22번으로 훌쩍 증가하는 것을 볼 수 있습니다.

이는 피보나치 수를 작은 수들로 나누는 과정에서 중복 호출되는 함수가 많아지기 때문입니다. $f(7) = f(6) + f(5)$인데, 또 $f(6) = f(5) + f(4)$ 가 되니 벌써 $f(5)$가 두 번 계산 되어야 하는 것이죠.

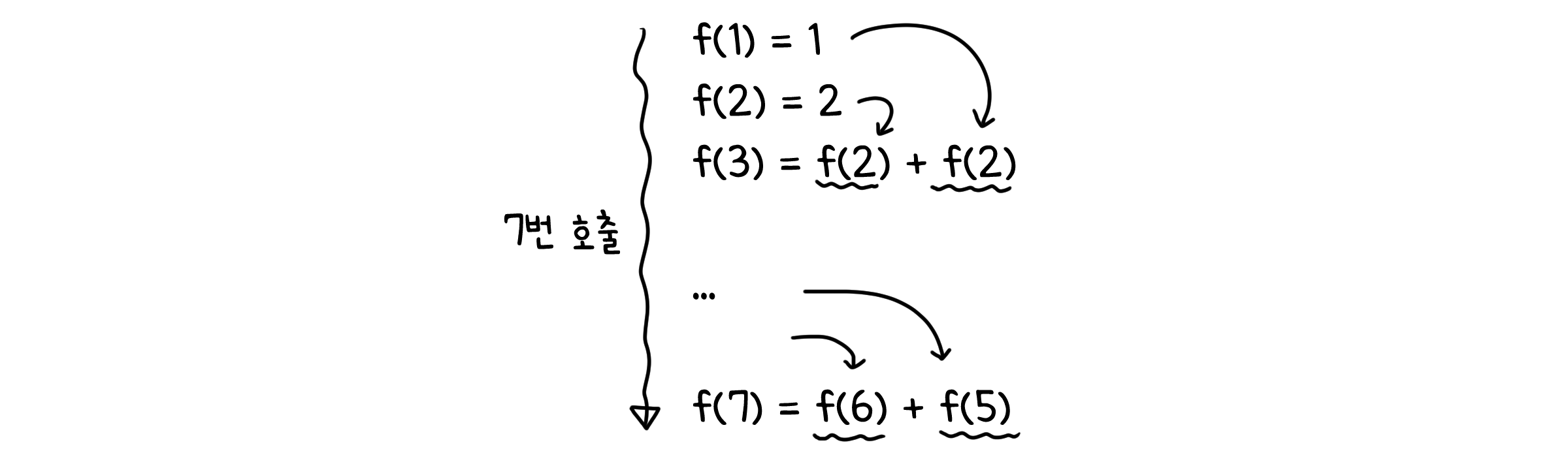
그래서 동적 계획법에서는 작은 문제들을 먼저 계산한 후, 이를 기억합니다. $f(3)$부터 미리 계산 해 놓으면 $f(4)=f(3)+f(2)$에서도, $f(5)=f(4)+f(3)$에서도, $f(3)$이 나올 때 마다 함수를 또 호출할 필요 없이 미리 계산된 값을 넣기만 하면 되니까요. 그리고 이렇게 계산한 $f(4)$, $f(5)$들로 값을 기억해 놓으면 또 써먹을 수 있습니다. 이렇게 값을 기억하는 방식을 메모이제이션(Memoization)이라고 합니다.

  
def Fibonacci_dp(n):
  memo = []
  
  for i := 1 to n:
    memo[i] = 0  # 초기값 0
  
  for i := 1 to n:
    if i <= 2:
      memo[i] = 1  # 기본값 f(1)=f(2)=1
    memo[i] = memo[i-1] + memo[i-2]  # 이미 기억한 값 사용하기
  
  return memo[n]

그래서 동적 계획법을 사용하면 아무리 숫자가 커져도, 피보나치 함수는 항상 $n$번만 호출하게 됩니다.

가장 긴 수열

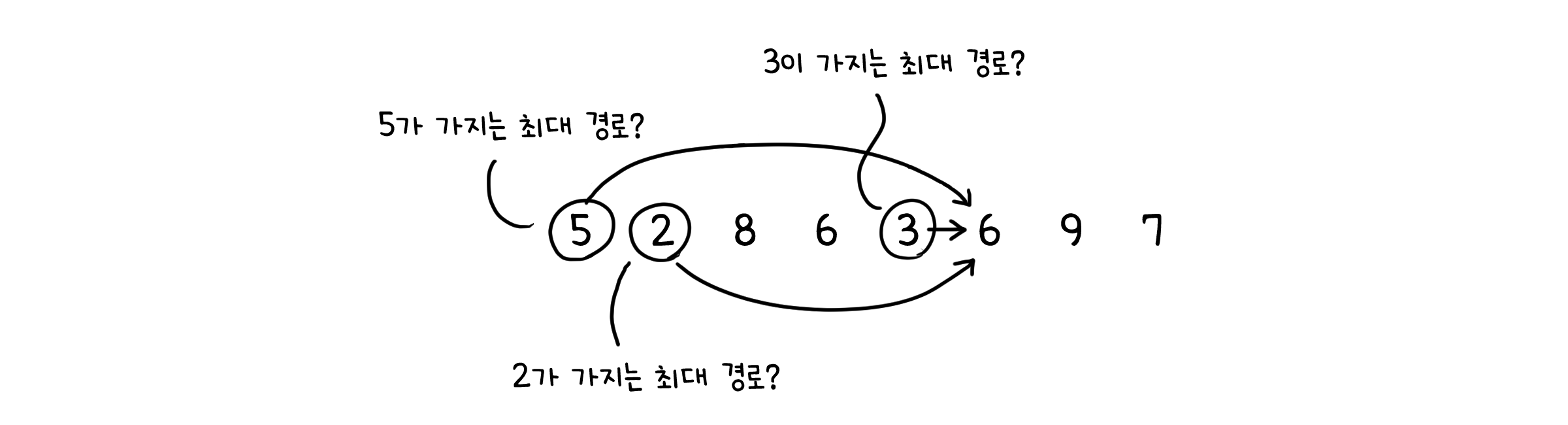
주어진 수열 $X={a_1, …, a_n}$이 있을 때, 그 안에서 가장 길이가 긴 증가 수열의 길이를 계산해봅시다. 여기서 증가 수열은 $X$에서 나열된 순서가 변하지 않아야 합니다.

우리는 이 수열을 방향이 있는 비순환 그래프(DAG)로 나타낼 수 있습니다. 각 수가 점이고, 수가 증가하는 방향으로 선이 연결되는 방식으로요.

이제 문제는 길이가 가장 긴 경로를 찾는 것으로 바뀌었습니다. $n$번째 점이 가질 수 있는 가장 긴 경로의 길이를 $L(n)$이라고 합시다. 이는 $n$번째 점 바로 이전에 올 수 있는 점이 가지는 최대 경로 + 1로 나타낼 수 있습니다. $n$번째 점에 대한 문제를 $n$번째 바로 이전에 오는 점들에 대한 문제로 나누었다고 할 수 있습니다.

이를 수식으로 나타내면,

\[L(i) = 1 + \max_{(i, j) \in E} \{ L(j) \}\]

마지막에는 모든 $j$에 대해서 가장 큰 $L(j)$값을 반환하기만 하면 됩니다.

  
def longest_increasing_subseq_dp(X=[1, ..., n]):
  E = DAG(X).edges  # X로 만든 DAG의 선들
  L = []  # 각 점에서 가장 긴 경로의 길이들
  
  for i := 1 to n:
    L[i] = 0  # 초기값 0
  
  for i := 1 to n:  # 처음부터 끝까지
    L[i] = 1 + max(L[j] for j := (j,i) in E)  # i이전에 오는 j들에 대한 최대 길이 + 1
  
  return max(L)  # L 중에서도 최대 길이 반환

이 알고리즘은 1번째 부터 $n$번째 까지 순회하는 동안 그래프의 모든 선을 한 번씩 방문하게 됩니다. 따라서 실행시간은 $T(L(i)) = O(|E|) = O(n^2)$이라고 할 수 있습니다.

물론, 실행시간이 $O(n^2)$보다 덜 걸리는 알고리즘을 고안해낼 수도 있습니다. 다만 여기서는 동적 계획법에 중점을 맞춰 알고리즘을 작성한다는 사실을 명심하기 바랍니다.

단어 사이의 거리

두 단어가 주어져 있습니다. 이 둘은 얼마나 가까울까요?

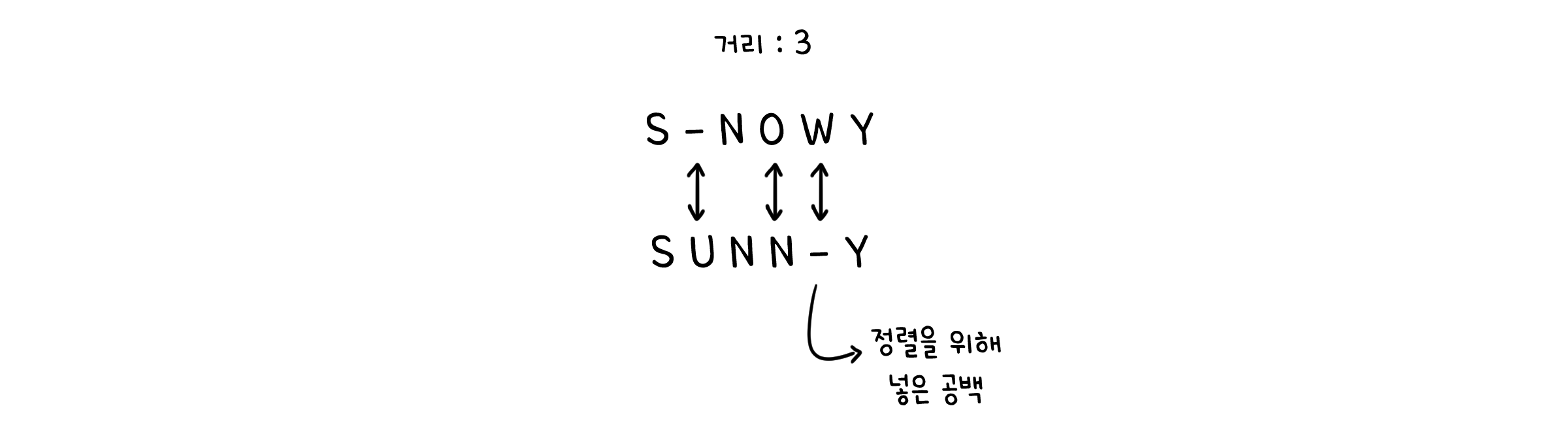
여기서 두 단어 사이의 거리는 두 단어가 겹치는 글자가 최대한 많도록 배열했을 때, 서로 다른 글자가 짝지어지는 횟수로 정의합니다.

이제 첫 번째 단어에서 글자를 추가하거나, 없애거나, 아니면 바꿔서 거리를 0으로, 즉 두 번째 단어로 바꿔보려합니다. 길이 $m$, $n$인 두 단어 $x$, $y$가 있을 때 최소한으로 필요한 수정 횟수 $E(m, n)$를 계산해봅시다.

우리가 생각할 수 있는 하위 문제는 맨 끝 문자를 수정하는 경우로, 나머지 문자들은 그대로 있고 오직 한 글자만 바뀐다고 생각하면 됩니다. 두 단어의 거리가 최소가 되도록 문자들을 잘 배치했을 때, 맨 끝 문자들은 총 세 가지 경우의 배치를 가지게 됩니다.

$x$의 문자만 있고 $y$는 공백 : $y$에 $x$의 맨 끝 문자를 추가하면 됩니다. 이 때 수정 횟수는 1입니다.
$y$의 문자만 있고 $x$는 공백 : $y$의 맨 끝 문자를 제거하면 됩니다. 이 때 수정 횟수는 1입니다.
$x$와 $y$의 문자가 모두 존재하는 경우 : 두 문자가 같다면 수정이 필요 없고, 다르다면 $x$의 문자를 $y$로 변환하면 됩니다. 이 때 수정 횟수를 $\text{diff}(m, n)$라고 정의합시다.

\[\text{diff}(m, n) = \begin{cases} 1 & \text{if } x_m \neq x_n \\ 0 & \text{if } x_m = x_n \end{cases}\]

세 가지 경우에 대해 각각 하위문제와 수정횟수를 합하면,

	추가	제거	변환
x	… x[m]	… [공백]	… x[m]
y	… [공백]	… y[n]	… y[n]
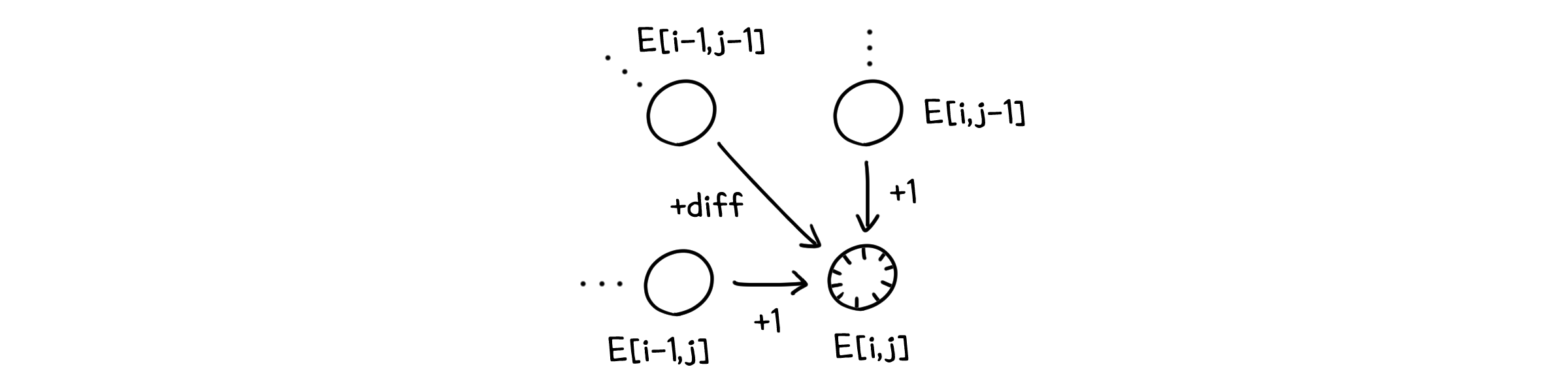
수정횟수	$E(m, n-1) + 1$	$E(m-1, n) + 1$	$E(m-1, n-1) + \text{diff}(m, n)$

따라서 우리는 $E(i, j)$를 이렇게 정의할 수 있습니다.

\[E(n, 0) = n, \; E(0, m) = m\] \[E(i, j) = \min{E(m, n-1) + 1, E(m-1, n) + 1, E(m-1, n-1) + \text{diff}(m, n)}\]

  
def edit_distance_dp(x[1, ..., m], y[1, ..., n]):
  for i := 0 to m:
    E[i, 0] = i  # 기본값
  for j := 0 to n:
    E[0, j] = j  # 기본값
    
  for i := 0 to m:
    for j := 0 to n:
      # 세 가지 경우 중에서 최솟값 선택
      E[i, j] = min(E[m, n-1] + 1, E[m-1, n] + 1, E[m-1, n-1] + diff(m, n))
  
  return E[m, n]

$x$의 처음부터 끝까지, 그리고 $y$의 처음부터 끝까지 순회하며 하위 문제들의 답을 채워야 하기 때문에, 실행시간은 $O(mn)$입니다.

배낭 문제 (Knapsack problem)

여러분에게 작은 배낭이 있고, 눈 앞에는 분명 돈이 될 것만 같은 반짝거리는 보석 장신구들이 뒹굴고 있다고 합시다. 여러분이 해야 할 일은 명확하겠죠.

관건은, 얼마나 높은 값어치를 가져갈 수 있느냐가 될 것입니다.

배낭 문제는 용량 $W$인 배낭이 있을 때, 각각 무게가 $w_i$, 가치가 $v_i$인 물건 $n$개 중 가장 높은 값어치로 가져갈 수 있는 조합을 구하는 문제입니다. 경우에 따라 물건에 개수 제한이 없거나, 최대 하나씩만 가져갈 수 있는 등 조건이 바뀌기도 합니다.

용량 $w$의 배낭에 최적의 조합을 챙겼을 때 총 값어치를 $K(w)$라고 합시다. 하위문제는 이미 물건 하나를 챙겼다고 가정했을 때, 남은 공간과 남은 물건에 대한 문제가 될 것입니다. 그리고 각 경우 중 최대값을 고르면 됩니다.

\[K(0) = 0\] \[K(w) = \max_{w_i \leq w}\{ K(w-w_i) + v_i \}\]

  
def knapsack(W: int, i[1, ..., n], w[1, ..., n], v[1, ..., n]):
  K = [0]
  
  for w := 1 to W:
    for i := 1 to n:  # 모든 물건에 대해
      if w[i] <= w:  # 만약 남는 공간 안에 들어갈 수 있으면
        K(w) = max(K(w), K(w-w[i] + v[i]))  # 그 물건을 선택했을 때와 기존 경우를 비교
  
  return K(W)

실행시간은 $O(nW)$가 됩니다.

동전 교환

여러분은 물건을 사려고 합니다. 하지만 애석하게도 주머니에는 동전들 밖에 없어요.

동전을 싹싹 긁어 어떻게든 원하는 금액을 만드려고 합니다. 이 때, 가능한 적은 개수의 동전으로 계산을 해내는 방법이 있을 것입니다.

금액이 $d_i$인 동전들이 있을 때($d_1 > d_2 > … > d_k = 1$), $j$원을 만들 수 있는 가장 작은 동전 갯수를 $C(j)$라고 합시다. 그렇다면 하위문제는 다음과 같이 나타낼 수 있습니다.

\[C(0) = 0\] \[C(j) = \min_{d}\{ C(j-d_i) + 1 \}\]

  
def coin_change_dp(n, d[1, ... k]):
  C[0] = 0  # 0원의 동전 개수는 0개

  for j := 1 to n:
    C[j] = infinite  # 초기화

    for i := 1 to k:  # 모든 종류의 동전에 대해
      if j >= d[i]:  # 금액이 동전보다 크면
        C[j] = min(C[j], 1 + C[j - d[i]])  # 기존 동전 개수와 d_i 동전을 썼을 때 개수를 비교
  
  return C

실행시간은 $\Theta(nk)$입니다.

cm301

알고리즘

동적 계획법 (Dynamic Programming)

가장 긴 수열

단어 사이의 거리

배낭 문제 (Knapsack problem)

동전 교환

인기 태그