[CM301] 08. 탐욕적 알고리즘 (Greedy Algorithm)

 이때까지 정렬, 탐색, 경로 등을 거치며 다양한 알고리즘들을 소개하였습니다. 이들은 원리나 목적이 조금씩 다르지만, 공통된 전략을 공유하는 경우도 있었습니다. 퀵정렬과 병합정렬은 다른 알고리즘이지만 둘 다 문제를 작은 문제로 분할하는 회귀 방법을 사용하는 것 처럼요.

 이렇게 알고리즘들이 공유하는 하나의 설계 철학을 알고리즘의 디자인 패러다임이라고 합니다. 앞서 예시를 들었듯, 우리는 이미 하나의 디자인 패러다임인 분할 정복(Divide & Conquer)를 살펴 본 바 있습니다.

 이번에는 또 다른 디자인 패러다임인 탐욕적 알고리즘(Greedy Algorithm)과 이를 사용한 다양한 알고리즘들에 대해 다뤄보려고 합니다.

작성된 모든 코드는 Python의 형식을 빌린 유사 코드이며, 문법을 다소 무시한 부분이 있기 때문에 실행이 되지 않습니다.

탐욕적 알고리즘 (Greedy Algorithm)

 탐욕적 알고리즘은 선택의 때마다 지금 이 순간에 최적인 답을 선택한다는 철학의 패러다임입니다. 궁극적으로 최적의 선택인지는 모르지만, 당장에는 최적의 선택이니 옳다고 믿는 것입니다.

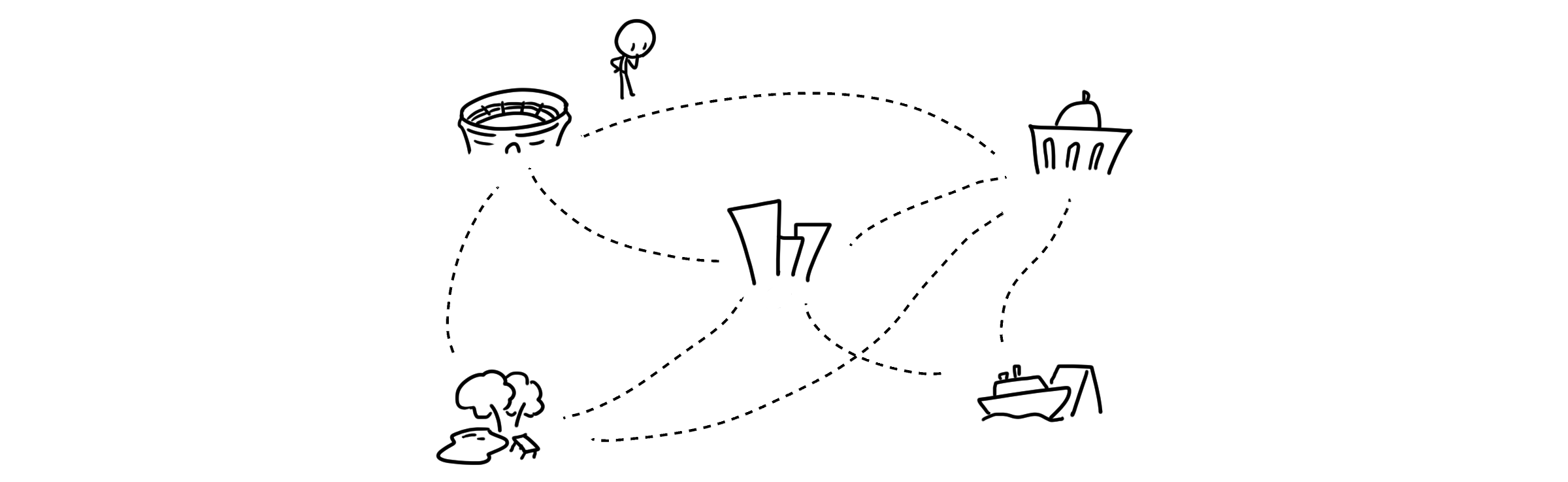
 여러분이 도시의 도로를 낸다고 생각해봅시다. 도로를 통해 모든 주요 지점들을 방문할 수 있어야 하니 점들은 서로 연결되어 있어야 합니다. 그리고 비용을 최소로 하면 좋으니 가능한 저렴한 비용의 도로를 최소한으로 놓고 싶겠죠.

 이렇게 가중치를 최소로 사용하면서 모든 점이 연결되어 있도록 하는 그래프를 최소 신장 트리(Minimum Spanning Tree, MST)라고 합니다. MST를 구하는 방법을 여러가지가 있습니다. 그릴 수 있는 모든 경우의 그래프를 그려 그 가중치를 비교하거나, 다익스트라나 벨만-포드 같은 복잡한 알고리즘을 사용해 볼 수도 있습니다.

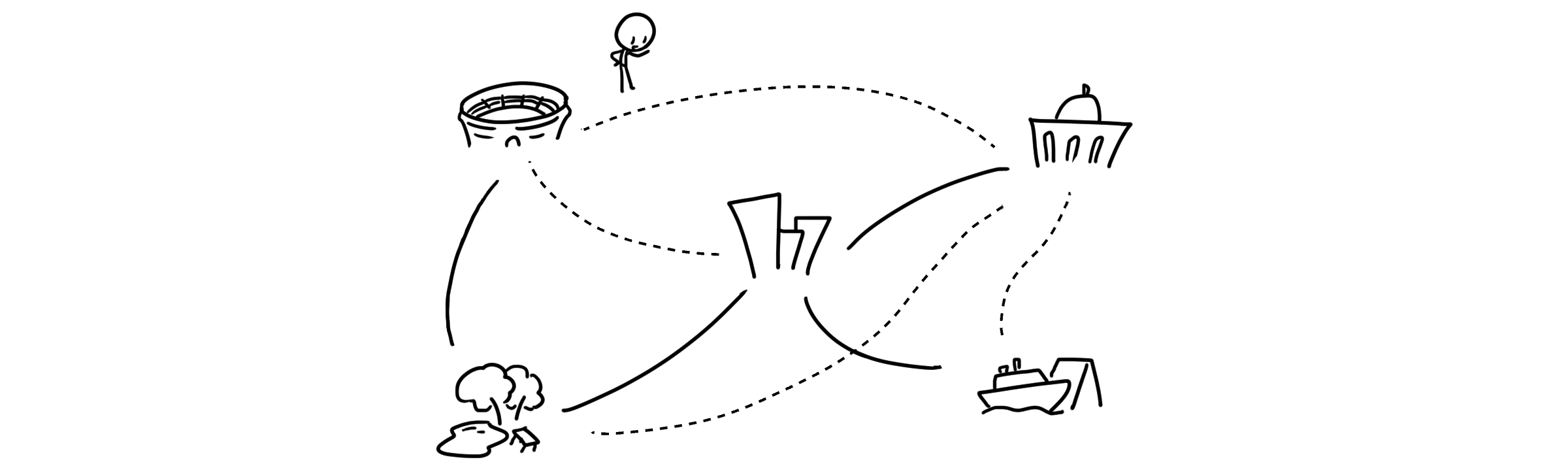
 하지만 단순하게 내가 있는 지점에서 가장 작은 가중치를 가지는 선만 선택하는 방법, 즉 탐욕적 알고리즘을 사용할 수도 있습니다.

 탐욕적 알고리즘을 사용할 때 주의해야 할 점은, 매 선택이 그 순간에서는 최적이지만 종합적으로도 그렇다는 보장을 할 수 없다는 것입니다. 따라서 알고리즘이 완전히 이상적인 결과만을 도출하지 않음을 명심해야 합니다.

크루스칼 알고리즘 (Kruskal’s Algorithm)

 크루스칼 알고리즘은 탐욕적 알고리즘을 통해 MST를 생성하는 방법 중 하나로, 순환을 만들지 않는 선에서 가장 작은 가중치의 선들을 선택해 연결해나가는 방식입니다.

# 보조 함수들 #
# make_set(x: Vertex) : v만 존재하는 집합 {v}를 생성
# find(x: Vertex) : v를 포함하는 집합을 반환
# union(x: Vertex, y: Vertex) : u와 v를 각각 포함하는 집합을 합집합 연산

def Kruskal(G=(E,V): Graph):
  for u in V:  # 모든 점 u에 대해
    make_set(u)  # u만 존재하는 집합 {u} 생성
  
  X = {}  # MST를 담을 빈 집합 X 생성
  sort(E, key=E.weight)  # 선 E의 가중치에 대해 오름차순으로 정렬
  
  for e=(u, v) in E:  # 모든 선 e에 대해(오름차순으로)
    if find(u) != find(v):  # u와 v가 같은 집합에 속해 있지 않다면
      X.add(e)  # X에 e를 추가
      union(u, v)  # u와 v가 속한 두 집합을 합침

보조 함수들

 크루스칼 알고리즘에서 몇 가지 보조 함수들을 볼 수 있을 것입니다.

• make_set(x: Vertex) : v만 존재하는 집합 ${v}$를 생성

• find(x: Vertex) : $v$를 포함하는 집합을 반환

• union(x: Vertex, y: Vertex) : u와 $v$를 각각 포함하는 집합을 합집합 연산

 이들은 모두 점들의 집합과 관련된 함수들입니다. 그래서 집합을 구현해야 하는데, 여기에 트리(Tree) 형태의 데이터 구조를 사용할 것입니다.

 이 트리는 실제 MST를 나타내는 데 사용하는 트리가 아니라, 알고리즘 상 점들의 집합 $X$를 구현할 때 사용하는 데이터 구조임을 명심해야 합니다.

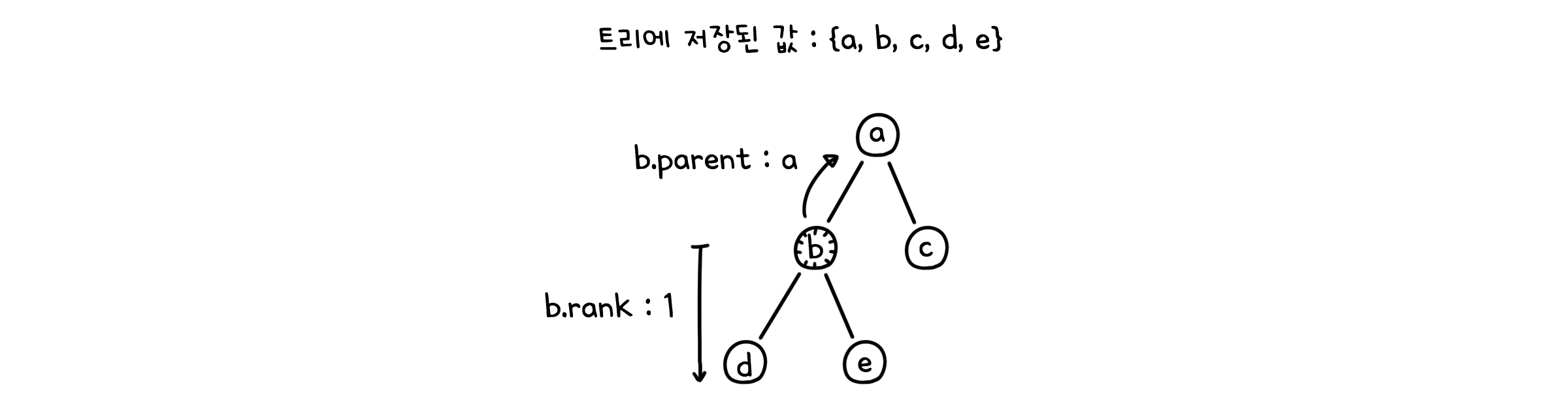
make_set( )

def make_set(x: Vertex):
  x.parent = x  # x 하나 밖에 없으므로 자기 자신이 루트
  x.rank = 0

find( )

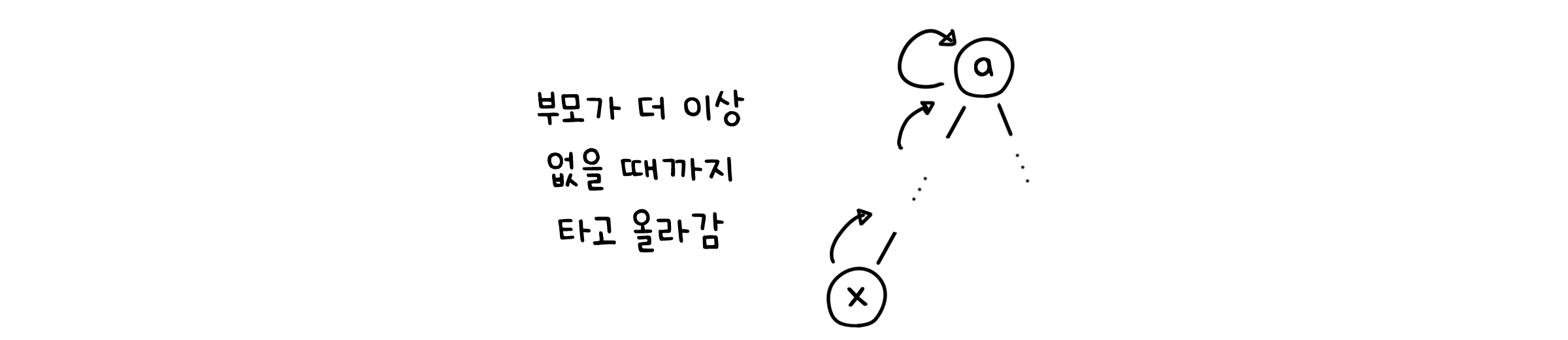
def find(x: Vertex):
  while x.parent != x:  # 부모가 더 이상 없을 때까지
    x = x.parent  # 부모를 타고 위로 올라감
  return x

union( )

def union(x: Vertex, y: Vertex):
  rx = find(x)  # x이 속한 집합의 루트
  ry = find(y)  # y가 속한 집합의 루트

  if rx == ry:  # 만약 두 집합이 같다면
    return  # 종료

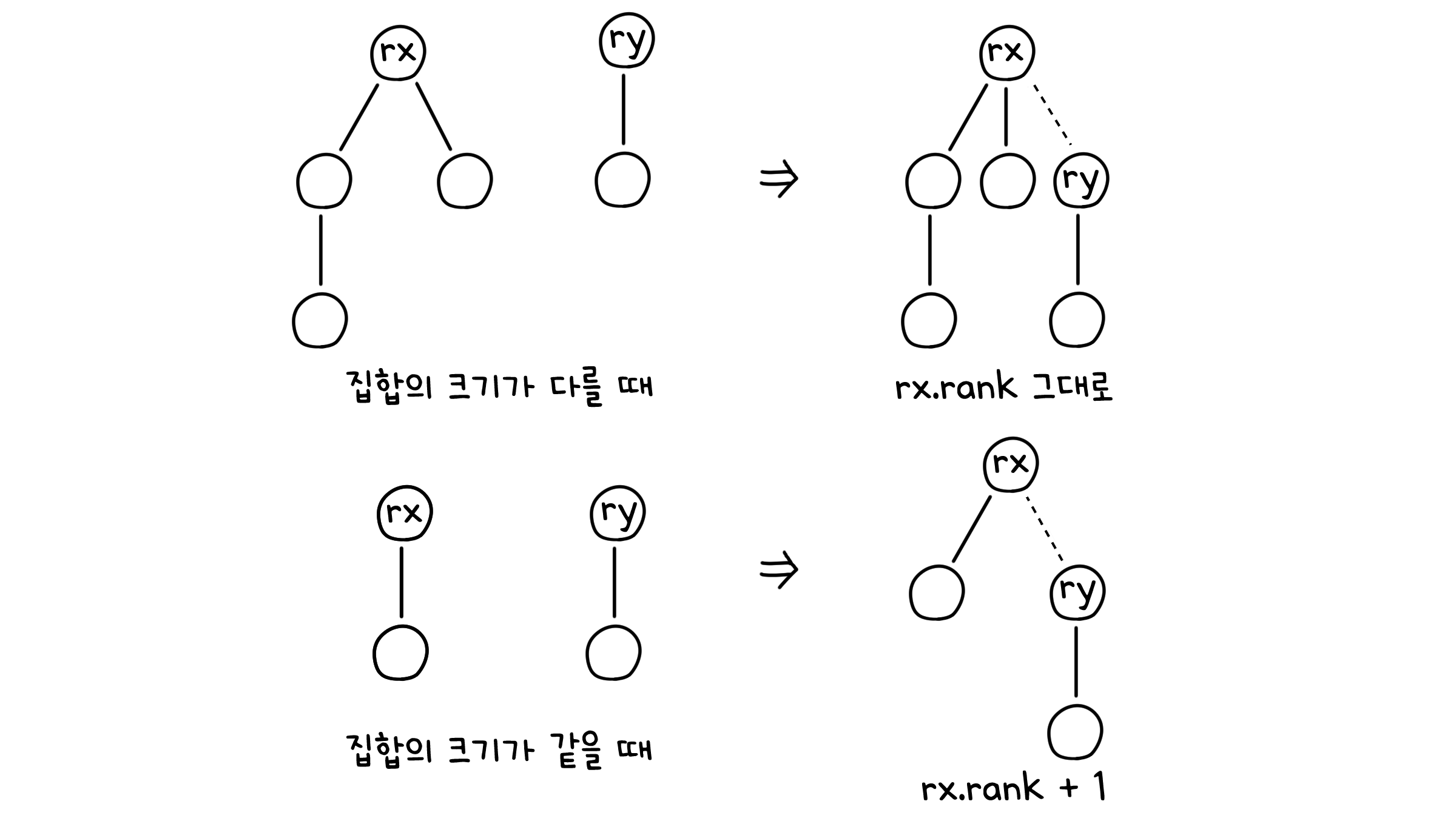
  if rx.rank > ry.rank:  # x 집합의 높이가 y 집합보다 크다면
    ry.parent = rx  # y 집합이 rx의 자식으로 들어감

  else if rx.rank < ry.rank:  # y 집합의 높이가 x 집합보다 크다면
    rx.parent = ry  # x 집합이 ry의 자식으로 들어감

  else:  # 두 집합의 크기가 같다면
    rx.parent = ry  # x 집합이 ry의 자식으로 들어감
    ry.rany += 1  # ry의 크기는 1 만큼 늘어남

절단 성질 (Cut Property)

 크루스칼 알고리즘의 정당성을 논하기 전에, 증명에 사용할 절단 성질(Cut Property)에 대해 먼저 살펴보겠습니다.

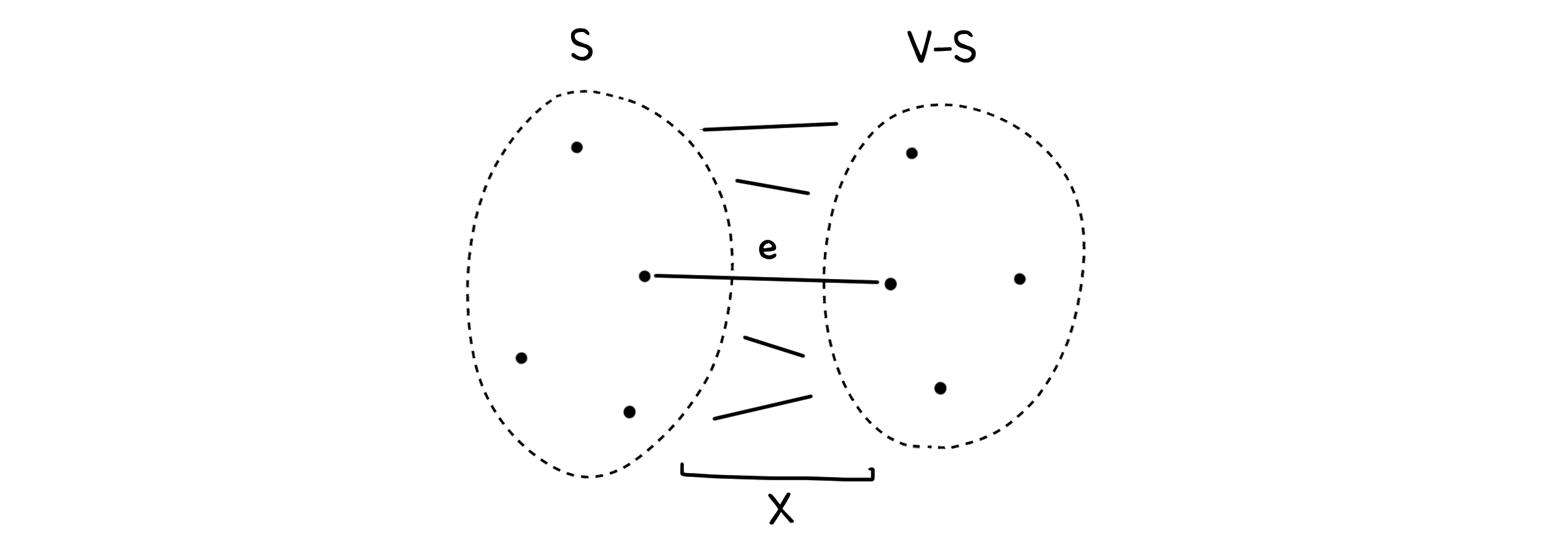
Theorem. 절단 성질(Cut Property)
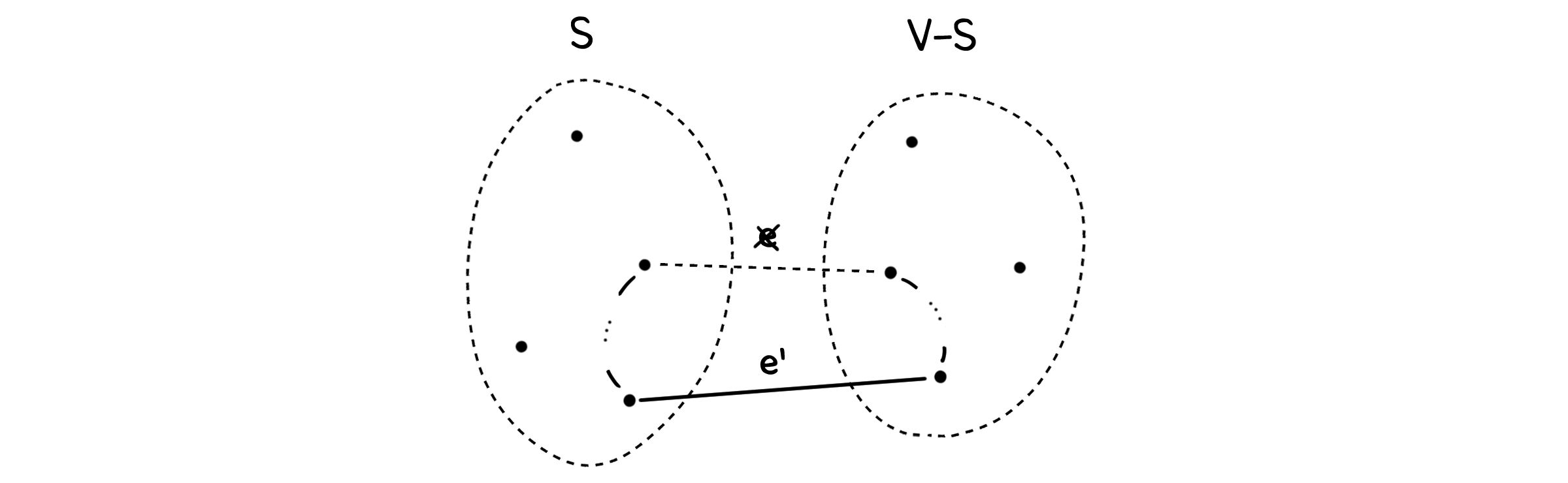
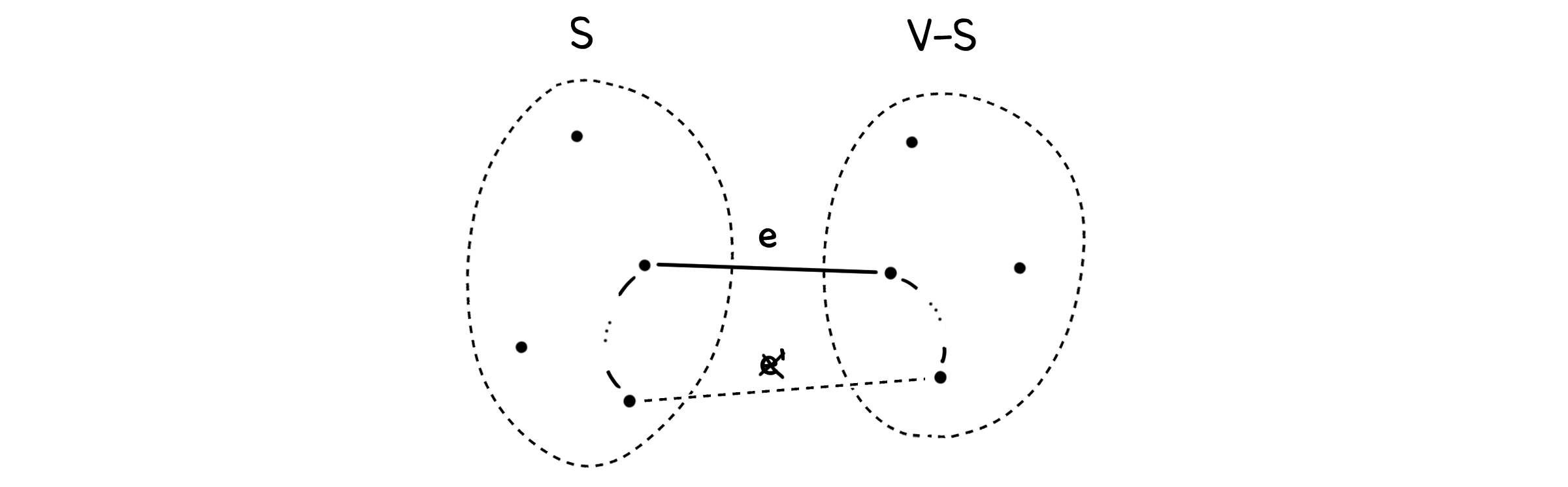
그래프 $G=(E, V)$가 주어졌을 때 $V$의 부분집합 $S \subseteq V$에 대해 $S$와 $V-S$에 속하는 점을 연결하는 선의 집합을 $X \subseteq E$라고 하자. $X$에 속한 선 중 가장 작은 가중치를 가진 선을 $e \in X$라고 할 때, $e$는 항상 MST에 포함된다.

 증명은 반증법으로 수행합니다. 만약 $e$가 포함되지 않은 MST $T’$가 존재한다고 가정합시다. $T$’에는 $e$대신 두 점을 연결하는 다른 선 $e’$가 존재할 것입니다.

 여기에 $e$를 집어 넣고 $e’$를 빼서 새로운 그래프 $T = T’ + {e} - {e’}$를 만들어봅시다.

 $e$가 $e’$ 대신 $S$와 $V-S$를 연결하기 때문에 $T$도 신장 트리(Spanning Tree)라고 할 수 있습니다. 그런데 $e$는 $X$ 중에서 가장 작은 가중치를 가지기 때문에

\[weight(e) < weight(e’)\]

 라고 할 수 있으며, $e$와 $e’$의 차이를 제외하면 다른 모든 선이 동일한 두 그래프 $T$와 $T’$ 또한

\[weight(T) < weight(T’)\]

 를 만족합니다. 이는 $T’$가 MST라는 가정에 위배되므로 모순이 발생합니다. 따라서, MST에는 항상 $e$가 포함되어야 합니다. $\Box$

크루스칼 - 정당성

 이제 크루스칼 알고리즘의 정당성을 증명해봅시다. 수학적 귀납법으로 접근합니다.

 기본 단계는 $X = \emptyset$일 때 입니다. 공집합은 당연히 MST의 부분 집합이므로, 정당합니다.

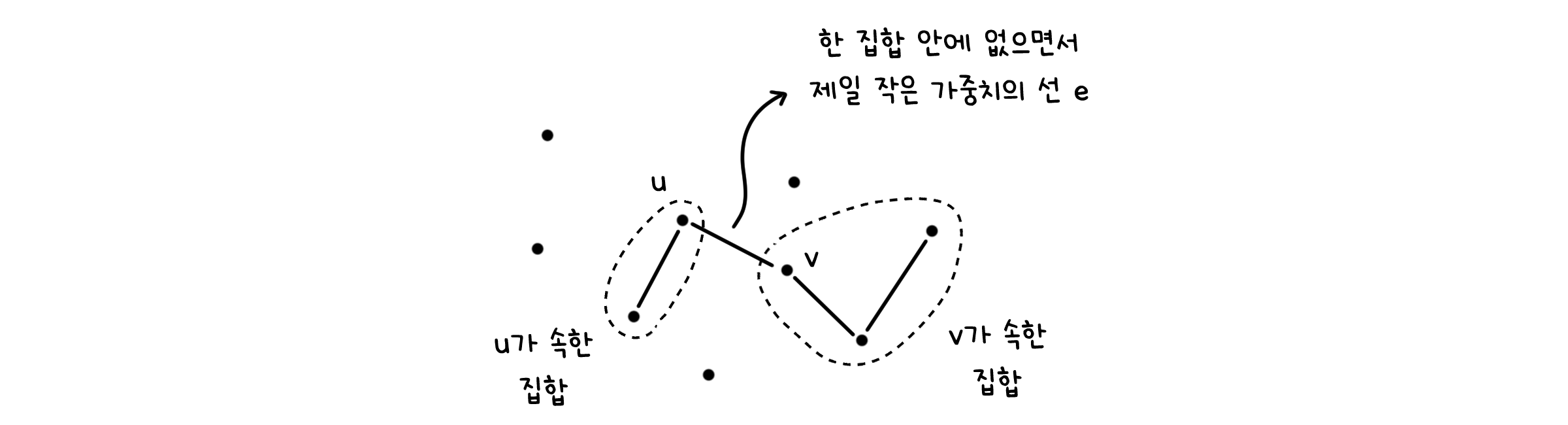
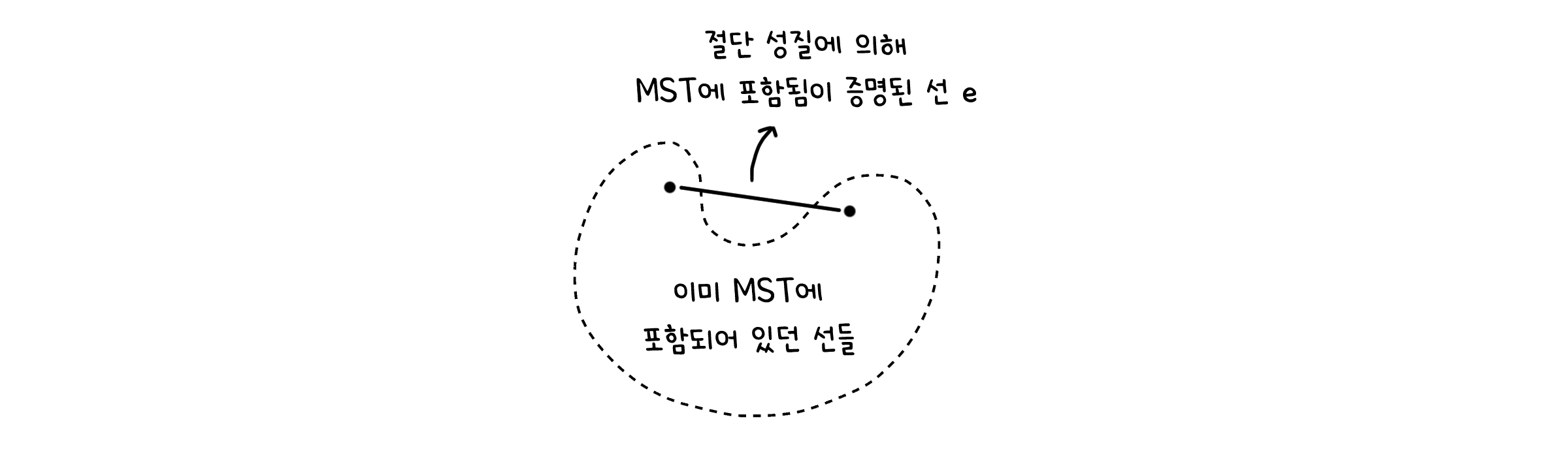
 귀납적 단계는 이때까지 선택한 $X$가 MST에 포함된 상태라고 가정합니다. 그 다음 선택되는 선 $e=(u, v)$는 $u$가 속한 점의 집합 $T_1$과 $v$가 속한 점의 집합 $T_2$를 연결하게 됩니다. 이 $e$는 아래 두 가지 특징을 만족합니다.

• 특징 1. 두 집합을 연결하는 선중 가장 작은 가중치를 가짐

• 특징 2. 서로 연결되지 않은 두 집합($T_1$, $T_2$)을 연결함

# ...
for e=(u, v) in E:  # 모든 선 e에 대해(오름차순으로) => 특징 1.
  if find(u) != find(v):  # u와 v가 같은 집합에 속해 있지 않다면 => 특징 2.
    # ...

 따라서 $e$는 절단 성질에 의해 MST에 포함되는 선이 됩니다. 또한 $e$가 새롭게 추가된 $X$ 도 계속 MST에 포함된 상태를 유지하게 됩니다.

 그러므로 수학적 귀납법에 따라 크루스칼 알고리즘에 의해 완성된 그래프 $X$는 MST라고 할 수 있습니다. $\Box$

크루스칼 - 분석

 크루스칼 알고리즘의 실행시간에 영향을 주는 연산은 앞서 소개한 보조 함수들이 있습니다.

• make_set(v) : 그저 $v$만을 가지는 집합을 만들 뿐이기 때문에, $O(1)$의 시간이 소요됩니다.

• find(v) : 최악의 경우 $v$가 트리의 말단에 있어 트리 높이 전체를 거슬러 올라야 합니다. 그리고 트리는 최대 $|V|$개의 점을 가질 수 있으므로, $O(height) = O(\log{|V|})$의 시간이 소요됩니다.

• union(x, y) : 실행시간에 영향을 주는 연산은 find(x)와 find(y) 뿐입니다. 따라서 $O(\log{|V|})$의 시간이 소요됩니다.

 각 함수들은 아래 횟수 만큼 호출됩니다.

• make_set(v) : 처음 각 점마다 집합을 하나씩 만들기 때문에 $|V|$번 호출됩니다.

• find(v) : 각 점마다 연결된 모든 점에 대해 반복문이 실행되어 총 $2|E|$번(방향이 없는 그래프) 호출됩니다.

• union(x, y) : MST의 선이 하나씩 확정될 때마다 호출됩니다. MST의 선의 개수는 $|V|-1$개 이므로, $|V|-1$번 호출됩니다.

 따라서 각 호출 횟수 만큼 함수의 실행시간을 계산해보면,

	실행시간	호출횟수	총 실행시간
make_set(v)	$O(1)$	$|V|$	$O(|V|)$
find(v)	$O(\log{|V|})$	$2|E|$	$O(|E|\log{|V|})$
union(x, y)	$O(\log{|V|})$	$|V|-1$	$O(|V|\log{|V|})$
총 합			$O(|E|\log{|V|})$

\[O(\|E\|\log{\|V\|})\]

 만큼의 시간이 필요합니다.

 보조 함수 말고도 살펴볼 부분이 있는데, 가중치의 오름차순으로 선들을 정렬하는 부분입니다. 우리는 앞서 정렬 알고리즘이 최소 $O(n\log{n})$의 시간이 걸린다는 것을 알아냈습니다(02. 알고리즘의 분석을 참고해주세요). 여기서 $n = |E|$니까, 정렬에 걸리는 시간은

\[O(\|E\|\log{\|E\|})\]

 가 됩니다. 여기서 $|V| \leq |E| \leq |V|^2$ 이니까, $\log{|V|} \leq \log{|E|} \leq 2\log{|V|}$, 즉 $\log{|E|} = O(\log{|V|})$ 입니다. 따라서 정렬도 동일하게

\[O(\|E\|\log{\|V\|})\]

 만큼의 시간이 필요합니다. 따라서, 크루스칼 알고리즘의 전체 실행시간은 \(O(\|E\|\log{\|V\|})\)입니다.

프림 알고리즘 (Prim’s Algorithm)

 프림 알고리즘은 탐욕적 알고리즘을 통해 MST를 생성하는 또 다른 방법입니다.

def Prim(G=(E,V): Graph):
  for u in V:  # 처음엔 어떠한 점도 방문하지 않음
    cost(u) = infinite
    prev(u) = None

  s = random(V)
  cost(s) = 0  # 시작점은 거리 0

  H = make_queue(V)  # 최솟값 큐 생성
  while H is not empty:
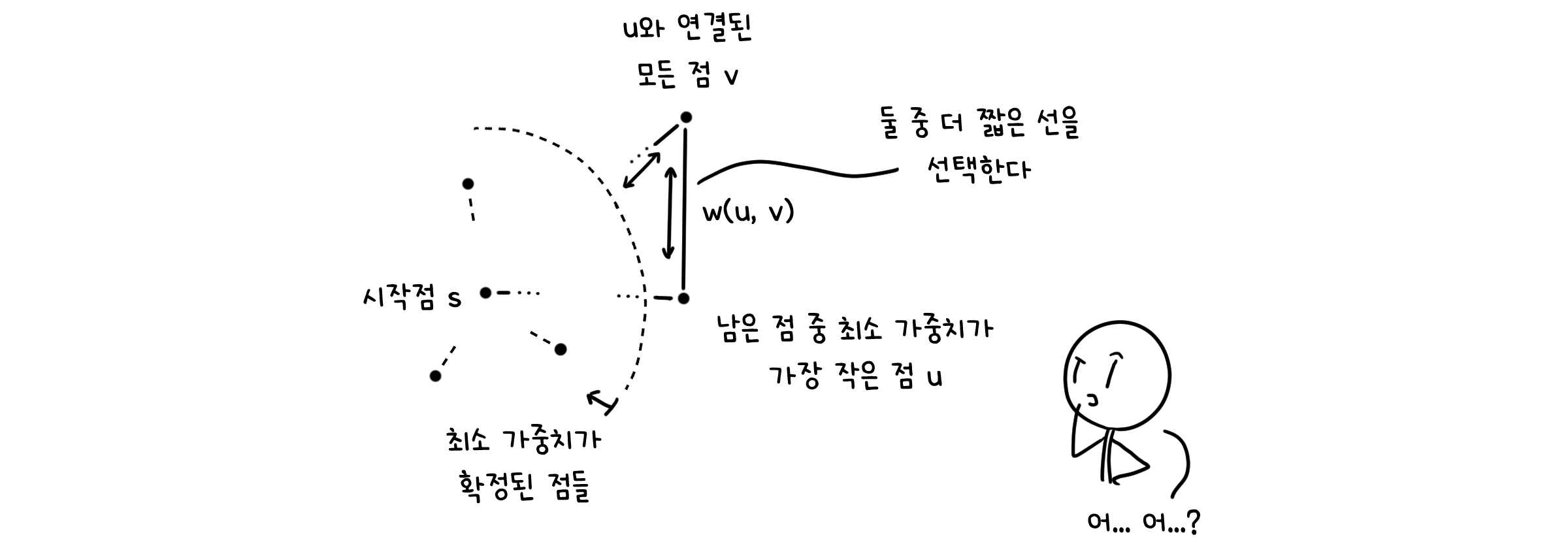
    u = H.delete_min()  # 남은 점 중 가장 가중치가 작은 점 u

    for e := (u, v) in E:  # u와 연결된 모든 점 v에 대해
      if cost(v) > l(u, v):  # 기존 최소 가중치보다 더 작은 가중치가 나오면
        cost(v) = w(u, v)  # v의 최소 가중치 갱신
        prev(v) = u  # 최소 가중치로 연결된 점은 u가 됨
        H.decrase_key(v)  # v의 거리 갱신

 이거… 어디서 많이 보지 않았나요?

 다익스트라 알고리즘과 거의 똑같이 생겼습니다. 실제로 최적값을 확정짓는 확정집합 $R$을 서서히 넓혀가는 방법, 그 기준으로 매번 가장 작은 값을 가지는 점을 고른다는 것 까지 동일한 전략을 사용합니다. 딱 하나, 다른 부분은 이곳입니다.

# 다익스트라
if dist(v) > dist(u) + l(u, v):  # 기존 거리보다 u를 거치는 경로의 길이가 더 짧으면
  dist(v) = dist(u) + l(u, v)  # v의 거리 갱신

# 프림
if cost(v) > l(u, v):  # 기존 최소 가중치보다 더 작은 가중치가 나오면
  cost(v) = w(u, v)  # v의 최소 가중치 갱신

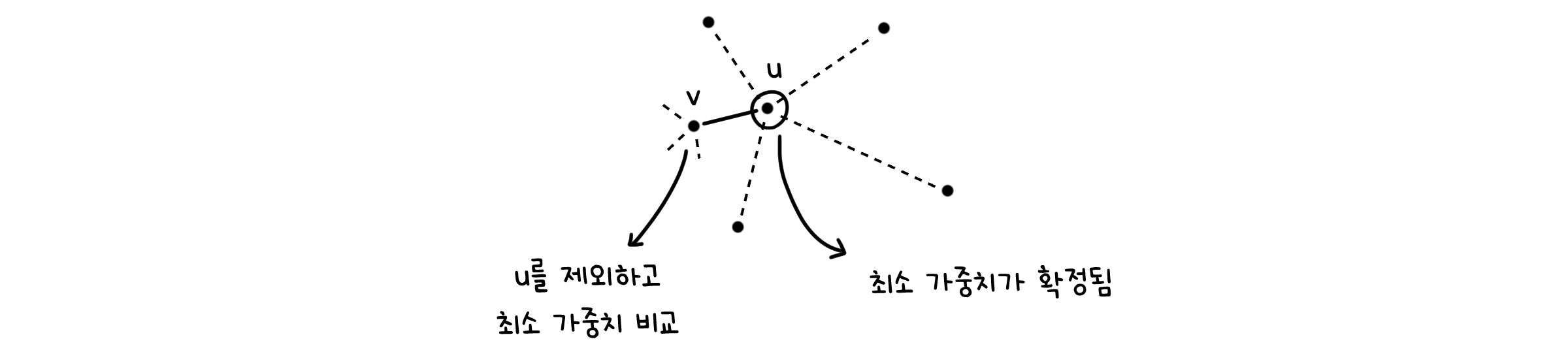
 다익스트라와 프림 알고리즘은 서로 최적화하는 값이 다릅니다. 점 $v$에 대해 다익스트라 알고리즘은 시작점에서 $v$ 까지의 최단 길이를 측정하는 반면, 프림 알고리즘은 $v$와 연결된 선 중 최단 길이를 최적화 대상으로 삼습니다.

 이렇게 하면 모든 점은 자신과 연결된 최소 가중치의 선을 하나씩 가지게 됩니다. 이는 곧 모든 점이 적어도 다른 한 점과 연결되어 있다는 뜻이고, 최소 가중치 선을 가진 점은 이후 탐색에서 제외되므로 중복 선택될 가능성도 없습니다. 따라서 프림 알고리즘을 통해 모두 연결되어 있고 최소 가중치를 사용하는 그래프, 즉 MST를 만들 수 있습니다.

 더해서 다익스트라 알고리즘과 동일한 전략을 사용하기 때문에, 실행 시간 또한 똑같이 $(|V|+|E|)\log{|V|}$(이진 힙을 사용할 때를 가정합니다)가 됩니다.

호프만 인코딩 (Huffman Encoding)

 호프만 코딩(Huffman coding)은 특정 값을 기준으로 요소들을 정렬하고자 할 때, 최소한의 비트만을 사용하여 일련번호를 부여하는 방법입니다. 주로 특정 값은 요소의 사용 빈도가 되고, 자주 사용되는 요소일수록 짧은 일련번호를, 잘 쓰이지 않는 요소는 긴 일련번호를 부여하는 식입니다.

요소	빈도	일반 코드	호프만 코드
A	70	00	0
B	3	01	001
C	20	10	01
D	37	11	11

 하지만 위 같은 경우 001을 해석할 때 0과 01로 읽을 수도 있고 001로 읽을 수도 있는 혼동이 있습니다. 그래서 중의적으로 해석할 여지가 없도록, 둘 이상으로 쪼개질 수 없는 코드가 되어야 합니다.

요소	빈도	일반 코드	호프만 코드 (진짜)
A	70	00	0
B	3	01	100
C	20	10	101
D	37	11	11

def Huffman(f[1, ..., n]):
  H = make_queue()  # 최솟값 큐 생성

  for i := 1 to n:  # 모든 f의 요소를
    H.insert(i)  # H에 추가
  
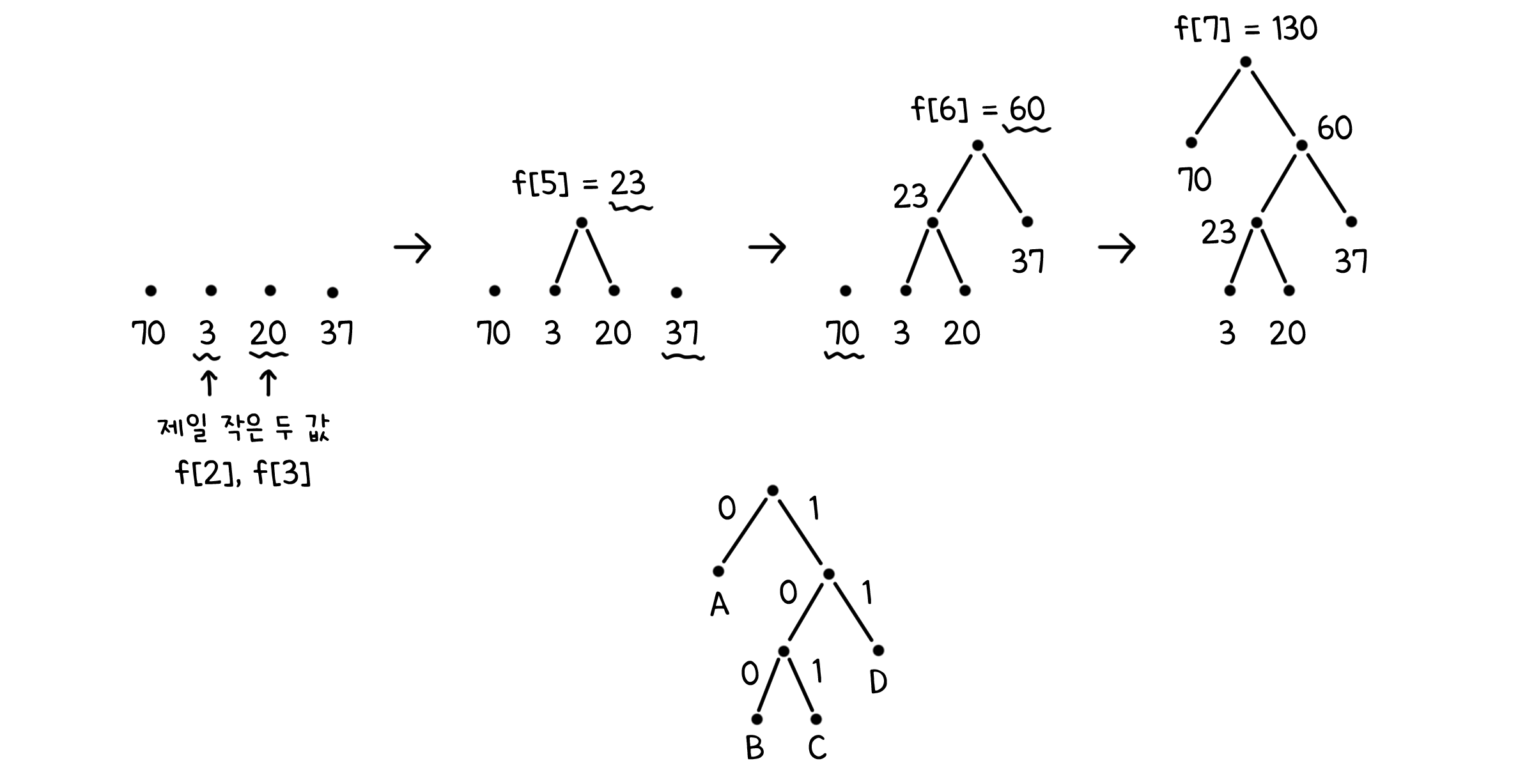
  for k := n+1 to 2n-1:  # n-1개의 추가 노드에 대해
    i = H.delete_min()  # 남은 것 중 첫 번째 최솟값
    j = H.delete_min()  # 남은 것 중 두 번째 최솟값
    
    f[k] = f[i] + f[j]  # i와 j를 자식으로 두는 부모 노드 생성

    H.insert(k)  # 최솟값 큐에 추가

 이렇게 트리를 쌓아 올리면 어느 코드도 둘 이상으로 쪼개질 수 없게 만들 수 있습ㄴ다. 빈도 수에 따라 비트도 최소한으로 사용할 수 있구요.

요소	빈도	일반 코드	호프만 코드
A	70	00 (2)	0 (1)
B	3	01 (2)	100 (3)
C	20	10 (2)	101 (3)
D	37	11 (2)	11 (2)
	비트수 $\times$ 빈도	260	213

계획 세우기 문제

 대학생활을 해본 적 있다면 수업 시간표를 직접 만들어본 경험이 있을 것입니다. 들어야 하는 과목은 많은데, 항상 수업시간이 겹치기 일쑤이죠.

 수업들이 겹치지 않으면서 최대한 많은 수업을 듣기 위해서는 신중히 선택해야 합니다. 이 문제도 탐욕적 알고리즘으로 풀어볼까요?

# S[] : 수업이 시작하는 시각
# F[] : 수업이 끝나는 시각

def Greedy_schedule(S[1, ..., n], F[1, ..., n]):
  X = []  # 선택한 수업들을 반환할 리스트

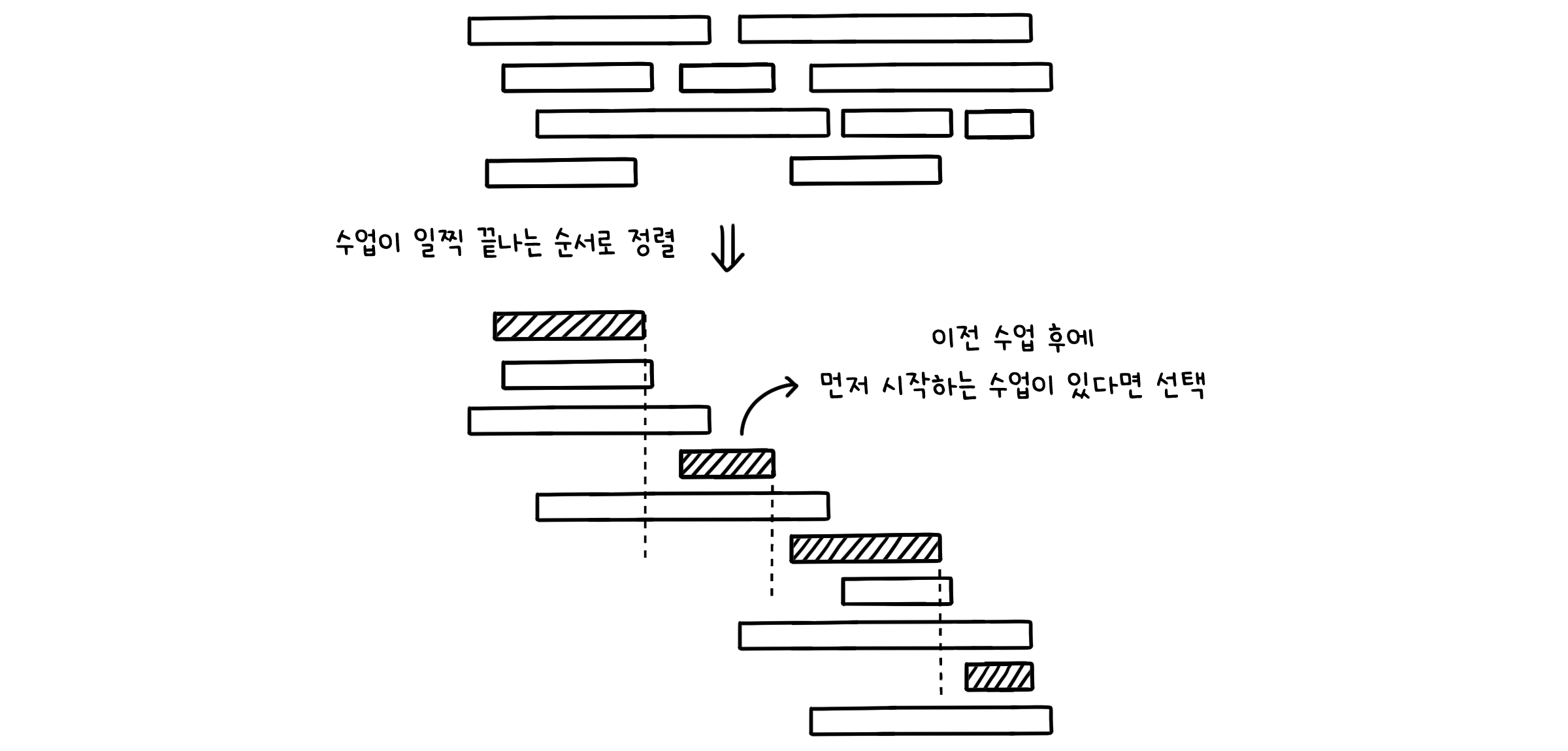
  sort(S, key=F[x])  # 수업이 일찍 끝나는 순서로 시작 시각 정렬
  sort(F, key=F[x])  # 수업이 일찍 끝나는 순서로 종료 시각 정렬

  count = 1  # 선택한 수업의 개수
  X[count] = 1  # 우선 첫 번째 수업을 선택하고 시작

  for i := 2 to n:  # 그 다음부터 마지막 수업까지
    if S[i] > F[X[count]]:  # 이전 수업 후에 먼저 시작하는 수업이 있다면
      count += 1  # 수업의 개수를 늘리고
      X[count] = i  # 그 수업도 선택
  
  return X[1, ..., count]

정당성

 다행히도 탐욕적 알고리즘 방법은 이 문제에서 최적의 답을 구할 수 있습니다. 위 방법은 수업이 끝나는 시각이 빠른 순으로 수업들을 순회하기 때문에, 이를 증명하면 됩니다.

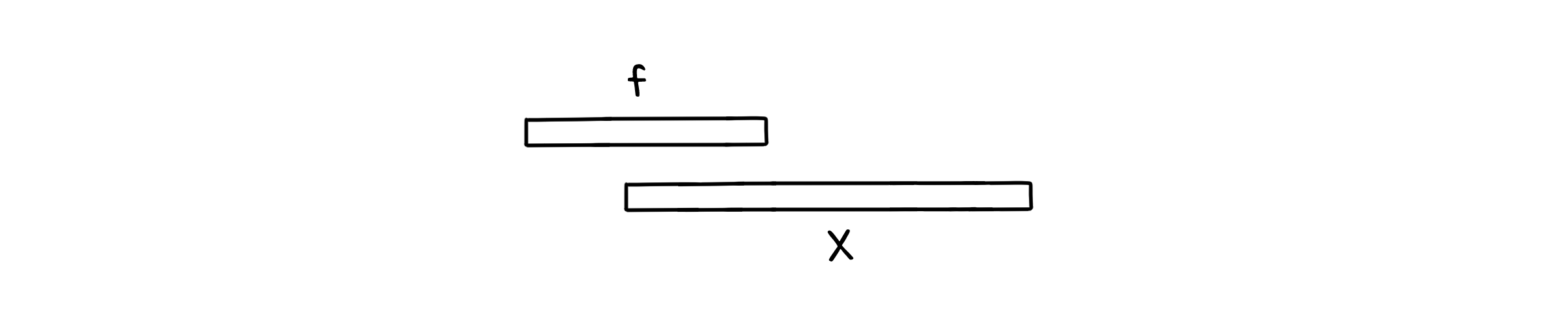
 가장 먼저 끝나는 수업을 $f$라고 할 때, $f$을 선택하지 않았지만 최적의 일정인 $X$가 있다고 가정합시다. 이 $X$는 $f$와 시간이 겹칠 수 밖에 없습니다. 만약 겹치지 않는다면, $X$에 $f$를 추가한 일정이 최적의 일정이 되어야 하니까요.

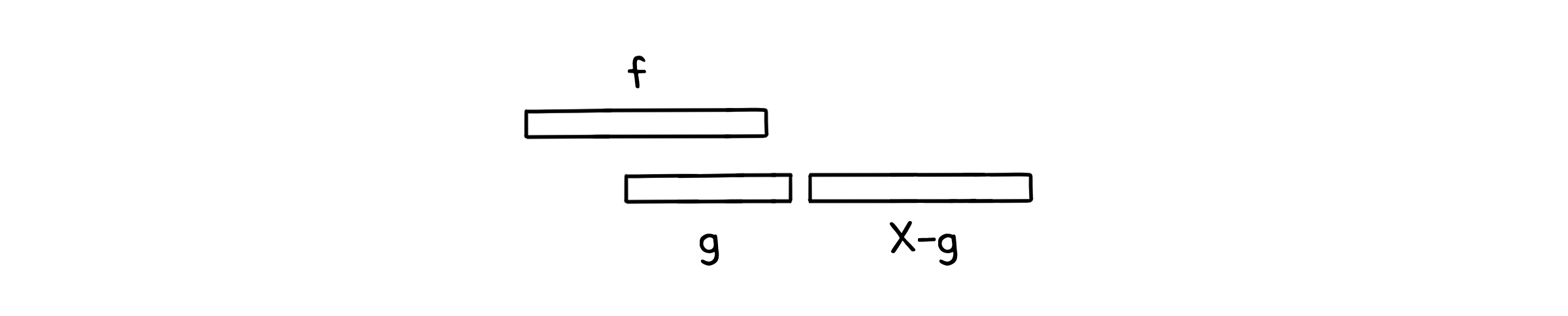
 $X$에는 $f$와 시간이 겹치는 일정 $g$가 존재하고, $f$는 가장 먼저 끝나는 수업이기 때문에 $g$는 반드시 $f$보다 늦게 끝나는 수업이어야 합니다. 따라서 $X - {g}$ 도 $f$와 시간이 겹칠 수 없습니다.

 그렇다면, $X$에 $g$ 대신 $f$를 넣은 일정 $X’$를 생각할 수 있지 않을까요? 하나가 빠지고 하나가 들어왔으니, 선택한 수업의 수는 변함이 없어 $X’$도 마찬가지로 최적의 일정이 될 것입니다. 따라서 이 방법으로 우리는 최적의 일정을 만들 수 있습니다.

 하루에 가능한 많은 수업을 듣는 것을 최적이라고 부른다면요.