포스트

[CM301] 07. 경로 (Path)

게시 업데이트
[CM301] 07. 경로 (Path)
[CM301] 07. 경로 (Path)
By
26 분정도 걸립니다
[CM301] 07. 경로 (Path)

가장 짧은 경로

 네비게이션은 항상 목적지까지 가는 최단경로를 안내합니다.

image1

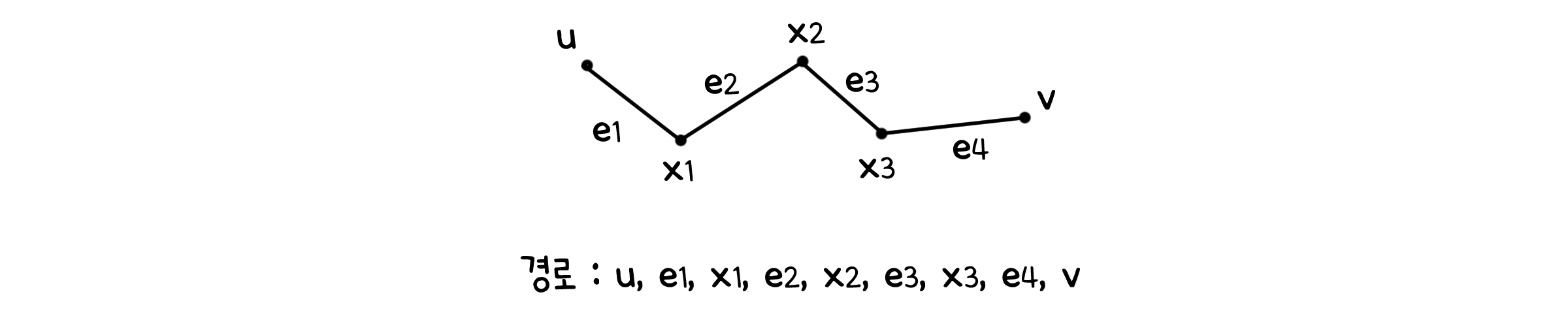
 최당경로를 구하는 문제는 그래프에서도 특별한 경우인 경로(Path)의 길이(Distance)를 구하는 과정입니다.

 그래프의 두 점 사이 경로(Path)는 점을 연결하는 선과 그 선으로 연결된 점을 번갈아가며 배열한 순서를 나타냅니다. 그리고 그래프의 두 점 사이 거리(Distance)는 그 사이에 존재하는 가장 짧은 경로의 길이로 정의합니다.

image2

 그럼 당연히 따라나와야 하는 질문이 있겠죠.

image3

 또 다른 알고리즘을 살펴볼 차례입니다.

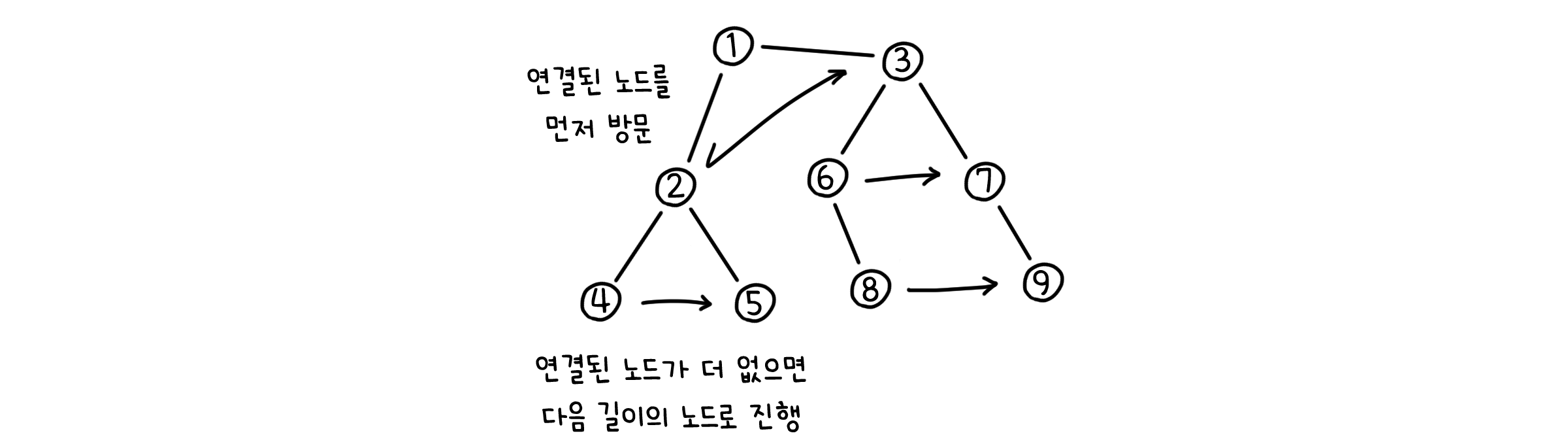
너비 우선 탐색 (Breath First Search, BFS)

  너비 우선 탐색(Breath First Search, BFS)은 그래프의 너비, 즉 연결된 노드들을 우선 탐색하는 그래프 탐색 방법입니다.

작성된 모든 코드는 Python의 형식을 빌린 유사 코드이며, 문법을 다소 무시한 부분이 있기 때문에 실행이 되지 않습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

def BFS(G=(E,V): Graph):
  for v in V:
    visited(v) = false  # 처음엔 어떤 점도 방문하지 않았음
	
  for v in V:  # 모든 점에 대해
    if not visited(v):  # 방문하지 않았다면
      Explore(v)  # 탐색을 실행

def Explore(v: Vertex):
  visited(v) = true  # 탐색을 시작하는 점을 방문 처리
  Q = Queue([v])  # v를 초기값으로 가지는 대기열 큐 생성
  
  while Q is not empty:
    u = Q.dequeue()  # 대기열에서 제일 오래된 값 뽑기
    for u := (u, w) in E:  # u와 연결된 모든 점 w에 대해
      if not visited(w)  # w를 아직 방문하지 않았다면
        Q.enqueue(w)  # 대기열에 추가
        visited(w) = true  # 방문 처리

image4

BFS - 정당성

 DFS때와 마찬가지로, 위 알고리즘이 정말 모든 점들을 탐색할 수 있는지 증명해봅시다.

image5

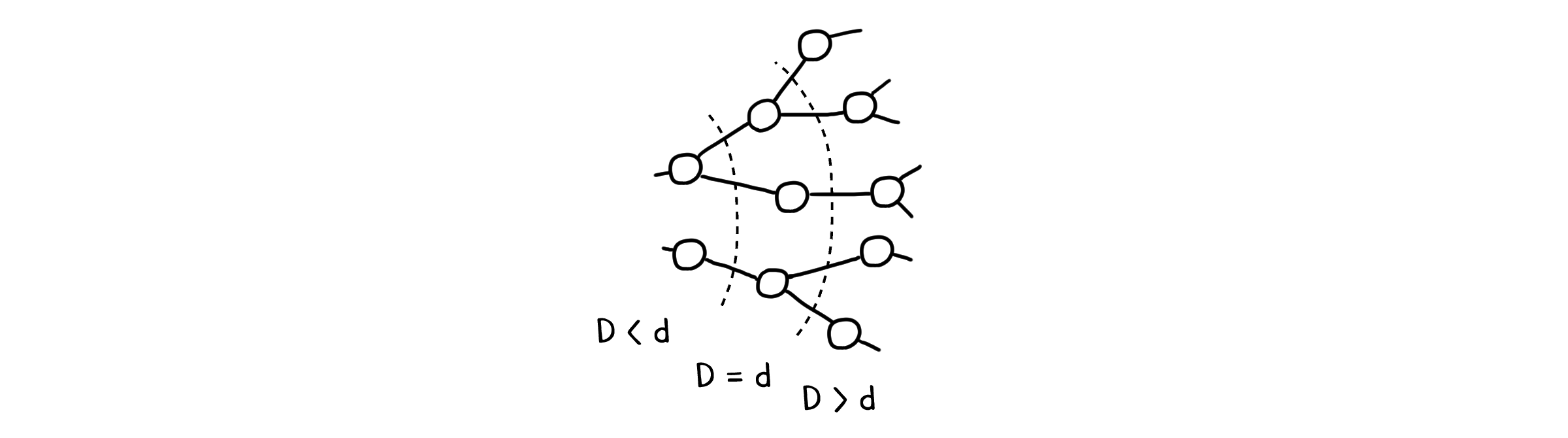
 수학적 귀납법을 사용합니다. 점들을 방문할 때마다 시작점으로부터의 거리 $D$를 기록한다고 가정합시다. 0 이상의 임의의 정수 $d$에 대해 현재 탐색중인 점의 거리가 $d$일 때, 그래프의 모든 점은 셋 중 한 경우에 해당해야 합니다.

  • $D < d$ 일 때 : 이미 Q에서 빠져나와 방문이 완료된 점입니다.

  • $D = d$ 일 때 : 현재 Q안에서 대기중인 점들입니다. Explore()는 Q가 빌 때까지 실행되기 때문에, 이들은 모두 빠져나와 방문이 완료될 것입니다.

  • $D > d$ 일 때 : 아직 방문되지 않은 점들입니다.

image5_1

 기본 단계는 $D=0$일 때입니다. 이 때는 Q에 시작점 $v$만 들어 있고, 나머지는 방문되지 않은 상태로 위 세 가지 조건을 만족합니다.

 귀납적 단계는 $D=d$일 때 위 세 가지 조건을 만족하는 상태라고 가정합니다. Q 안에 있는 점들은 빠져나오면서 연결된 다른 점($D=d+1$인)들을 Q에 집어 넣을 것입니다.

 Q안의 $D=d$점들을 모두 방문했다면 $D < d+1$인 점들은 모두 방문이 완료된 상태이고, $D = d+1$인 점들은 모두 Q 안에 있으며, $D > d+1$인 점들은 여전히 방문되지 않은 상태가 됩니다. 즉, $D=d+1$일 때도 세 가지 조건을 만족하므로 수학적 귀납법에 의해 정당성을 만족할 수 있습니다. $\Box$

BFS - 분석

 노드를 방문했는지 판단할 수 있는 visited 리스트를 둔 덕분에, BFS를 하는 동안 중복 방문을 피할 수 있습니다. 때문에 모든 점에 대해 enqueue 및 dequeue가 한 번씩 호출됩니다.

1
2
3
4
5
6

  while Q is not empty:
    u = Q.dequeue()  # dequeue 호출
    for u := (u, w) in E:
      if not visited(w)
        Q.enqueue(w)  # enqueue 호출
        visited(w) = true  # 방문 처리

 또한 점 $v$를 방문했을 때, Explore()는 그 점과 연결된 점들을 찾기 위해 반복문을 실행합니다. 이때 연결된 점들은 $v$와 연결된 선의 개수 만큼 존재합니다. 따라서 모든 점들을 순회했을 때 반복문은 총 $|E|$번(방향이 없을 때) 또는 $2|E|$번(방향이 있을 때) 실행될 것입니다.

1
2
3
4

  while Q is not empty:
    # ...
    for u := (u, w) in E:  # v와 연결된 모든 점 u의 개수만큼 반복
      # ...

 따라서 BFS의 실행시간은 $O(|E| + |V|)$이 됩니다.

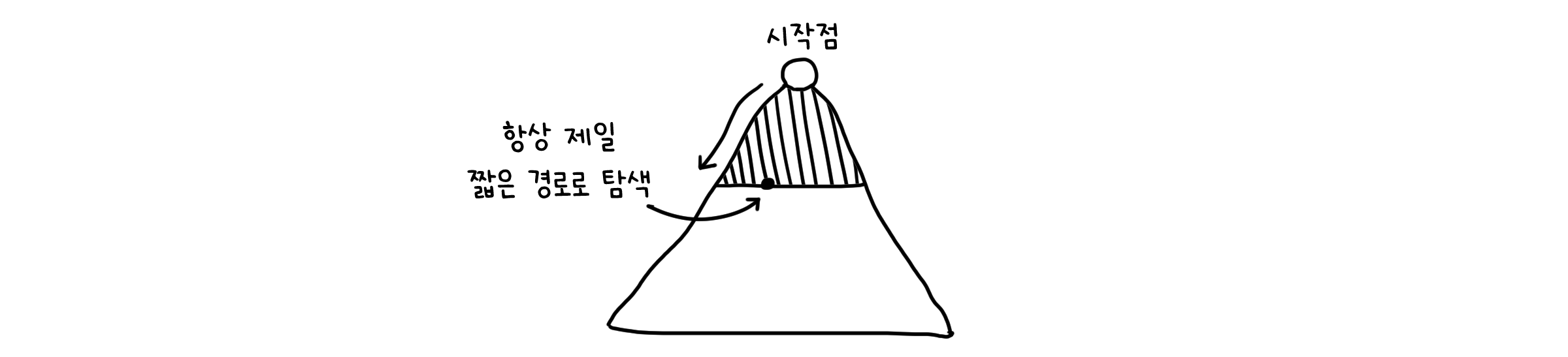
 BFS는 모든 점을 순회합니다. 따라서, 요소를 탐색하는데 BFS를 사용한다면 반드시 탐색을 완료할 수 있습니다.

 또한 DFS와 달리 탐색을 빠르게 해낼 수 있습니다. BFS는 시작점으로부터 거리 순서대로 탐색 범위가 넓어지기 때문에, 찾고자 하는 요소를 탐색한 시점에는 항상 최단 경로로 탐색을 마치기 때문입니다.

image6

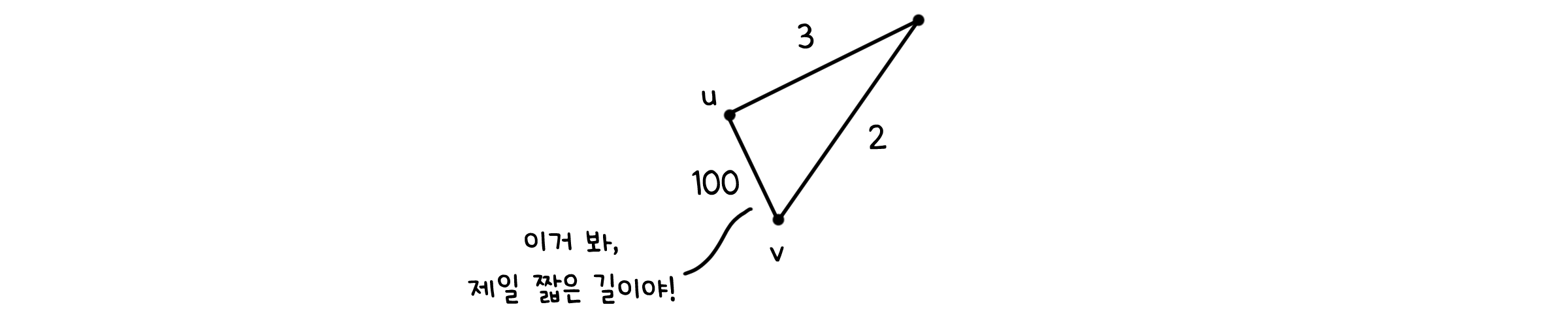
허점 - 가중치가 있는 그래프

 위 증명에 근거하여 BFS는 시작점으로부터 다른 점까지 이르는 최단 길이를 구할 수 있습니다. 하지만 치명적인 허점이 존재합니다. 이때까지 다룬 기본적인 그래프는 모든 선이 같은 크기의 가중치가 있었습니다. 어디를 가든 길이는 1만큼만 증가했죠. 만약에, 점과 점 사이의 선 마다 가중치가 다르면 어떻게 될까요?

image7

 BFS는 경로마다 거치는 선의 수만 알 뿐, 그 선이 어떤 가중치를 가지는가는 알지 못합니다. 이래서는 올바른 길을 고를 수 없어요. BFS를 좀 더 개선해야 할 필요가 있습니다.

다익스트라 알고리즘 (Dijkstra’s algorithm)

 네델란드의 컴퓨터 과학자 에츠허르 비버 다익스트라(Edsger Wybe Dijkstra)는 이 가중치 그래프의 최단 경로 문제에 대한 명료한 알고리즘을 고안해냈습니다. 이 알고리즘을 살펴보기에 앞서, 우리는 한 가지 개념을 먼저 짚고 넘어가야 합니다.

우선순위 큐 (Priority Queue, PQ)

 우선순위 큐(Priority Queue, PQ)는 선입선출의 원칙을 지키는 일반적인 큐와는 달리, 사용자가 지정한 우선순위에 맞춰 값을 빼낼 수 있는 데이터 구조입니다. 다익스트라 알고리즘은 큐에서 항상 최솟값을 골라 빼내는 최솟값 큐(min PQ)를 사용할 것입니다.

image8

우선순위 큐는 이진 힙 데이터 구조를 통해 구현할 수 있습니다. 우선순위 큐와 이진 힙에 대한 내용은 ‘데이터 구조’ 포스트에서 더 자세히 다루었으니, 살펴보기 바랍니다.

 다익스트라 알고리즘에서 사용할 최솟값 큐는 아래 메소드들을 가지고 있다고 가정하겠습니다.

메소드기능
make_queue($V$)시작점에서 점 들 $V$ 까지의 거리를 키값으로 하는 최솟값 큐를 생성합니다.
delete_min()큐에서 키값이 최솟값인 점을 빼내어 반환합니다.
decrease_key($v$)점 $v$의 키값을 감소한 값으로 갱신합니다.

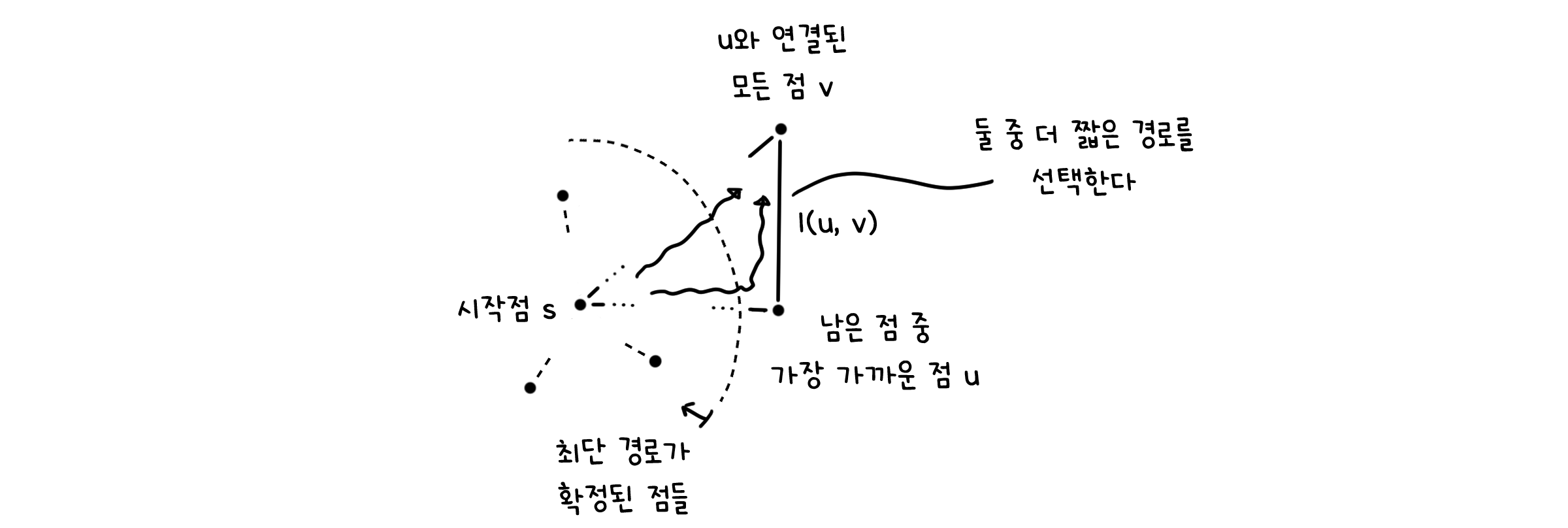
다익스트라 알고리즘

다익스트라 알고리즘은 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# l(u, v) : 점 u와 점 v 사이의 거리
# dist(x) : 시작점으로부터 점 x 까지의 최단거리
# prev(x) : 최단경로 상 점 x의 이전 점

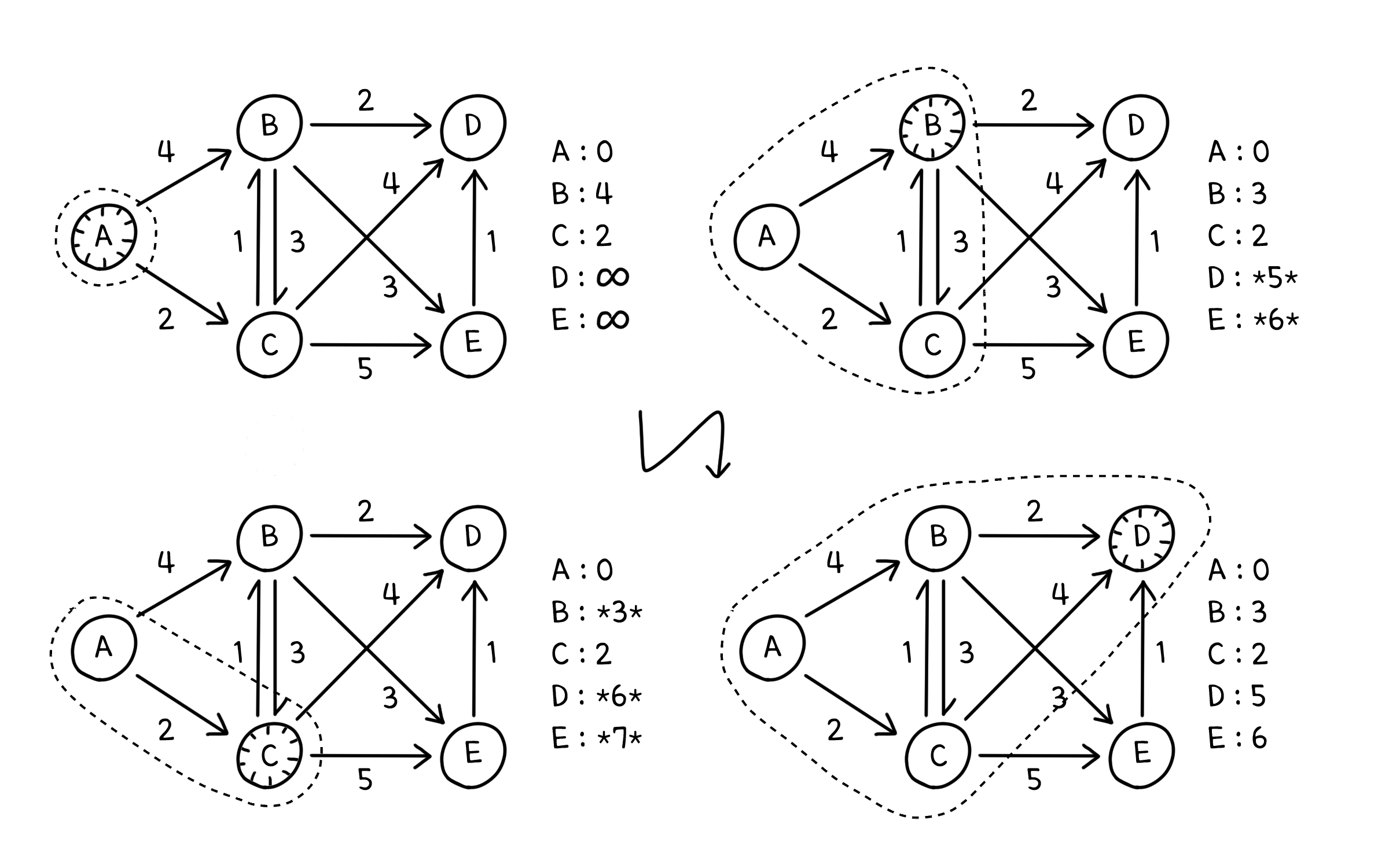
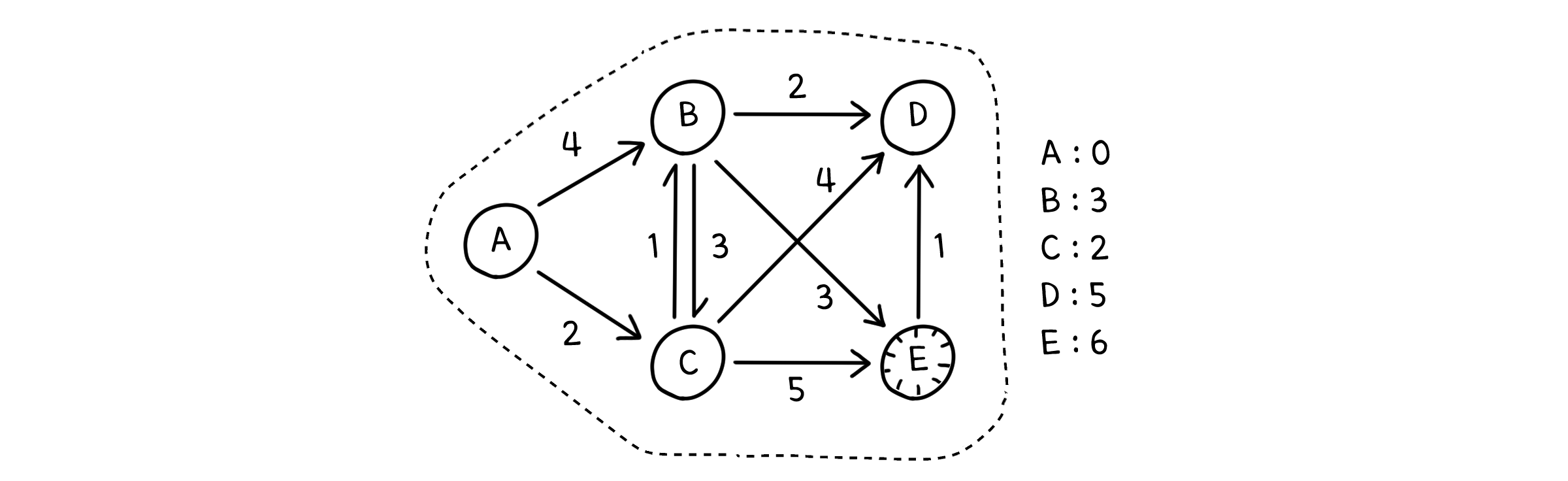
def Dijkstra(G=(E,V): Graph, s: Vertex):
  for u in V:  # 처음엔 어떠한 점도 방문하지 않음
    dist(u) = infinite
    prev(u) = None
  
  dist(s) = 0  # 시작점은 거리 0
  
  H = make_queue(V)  # 최솟값 큐 생성
  while H is not empty:
    u = H.delete_min()  # 남은 점 중 가장 가까운 점 u
    
    for v := (u, v) in E:  # u와 연결된 모든 점 v에 대해
      if dist(v) > dist(u) + l(u, v):  # 기존 거리보다 u를 거치는 경로의 길이가 더 짧으면
        dist(v) = dist(u) + l(u, v)  # v의 거리 갱신
        prev(v) = u  # v의 최단경로상 이전 점은 u가 됨
        H.decrease_key(v)  # v의 거리 갱신

image9

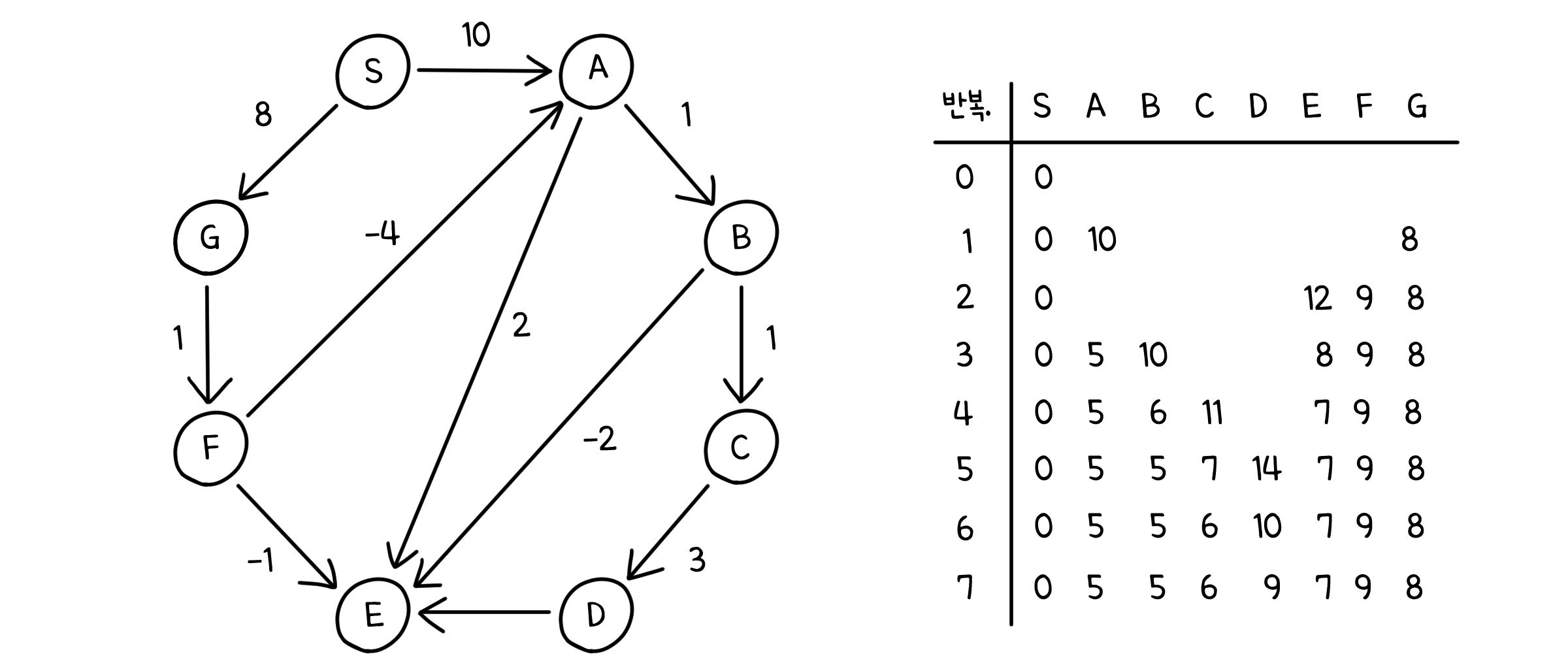
 예를 들어, 다익스트라는 아래와 같이 진행됩니다.

image10

image11

다익스트라 - 정당성

 우선 편의를 위해 점 $v$에 대해 실제 최단 길이를 $distance(v)$, 알고리즘이 진행되는 동안 계산하는 최단길이를 $dist(v)$라고 하겠습니다.

i) 목표 세우기

 우리가 최종적으로 보여야 할 사실은 다음과 같습니다.

image12

 하지만 이를 바로 증명하는 것은 어려우니, 조금 더 증명하기 쉬운 형태로 말을 바꿔야 할 필요가 있습니다.

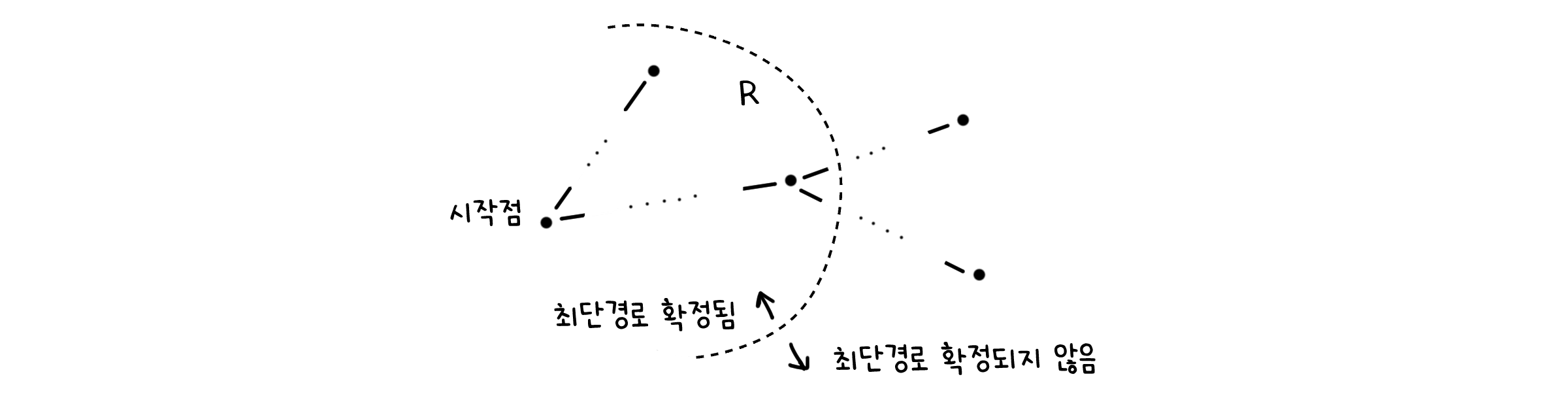
 알고리즘을 진행하다보면, $dist(v)$가 실제로 최단 길이를 가진다고 보장할 수 있는 순간이 있을 것입니다. 이 때 점 $v$는 확정 집합 $R$에 들어간다고 합시다. 확정집합 $R$에 있는 점들은 최단 길이가 확실히 밝혀진 점들로, 다익스트라 알고리즘이 종료되면 모든 점들은 $R$ 안에 들어가야 합니다.

image13

 따라서 우리의 목표는 이렇게 바꿀 수 있습니다.

image14

 이제 반증법으로 접근합니다. $R$에 들어가는 점들 중 최단거리를 가지지 않는 점 $u$가 생겼다고 가정합시다.

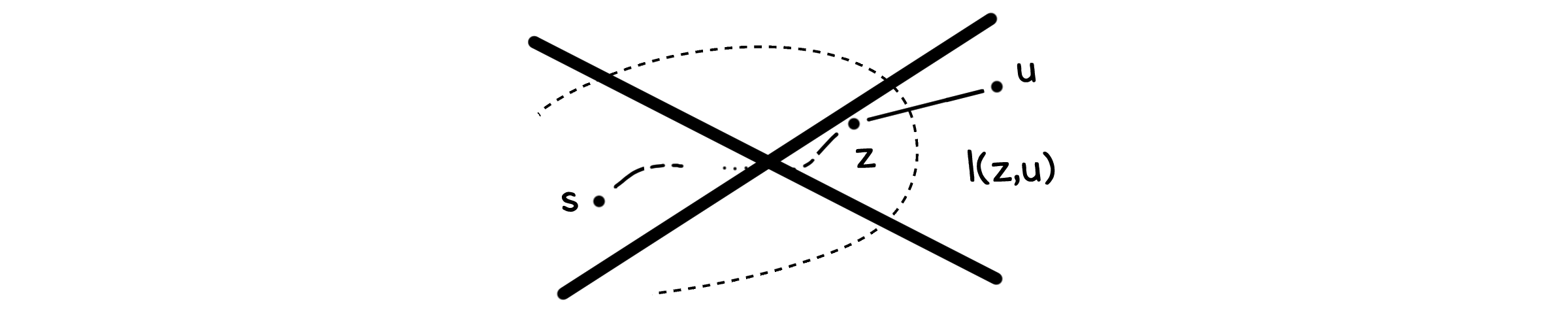
\[dist(u) > distance(u)\]

ii) 반증법 - $u$가 $R$ 바로 앞에 있을 때

 시작점에서 $u$까지 이르는 실제 최단경로에서 $u$ 바로 이전에 왔던 점을 $z$라고 합시다. 이 $z$가 이미 $R$ 안에 들어가 있는 상황, 즉 $u$와 $R$ 사이에 다른 점이 없는 상황이라고 가정할 수 있습니다.

image15

 $R$의 정의에 따라, $z$의 거리는 다음을 만족해야 합니다.

\[dist(z) = distance(z) \tag{a}\]

 한편, $u$의 거리는 알고리즘에 의해 이렇게 계산합니다.

\[dist(u) = min\{ dist(u), dist(z) + l(z, u) \}\]

 만약 $dist(u)$가 $dist(z) + l(z, u)$ 보다 작다면, $dist(u) < distance(z) + l(z, u) = distance(u)$가 됩니다. 이는 처음 가정이었던 $dist(u) > distance(u)$와 모순이 되기 때문에, 아래처럼 쓸 수밖에 없습니다.

\[dist(u) = dist(z) + l(z, u) \tag{b}\]

 $(a)$와 $(b)$를 합치면 이런 같은 결과를 얻을 수 있습니다.

\[dist(u) = dist(z) + l(z, u) = distance(z) + l(z, u) = distance(u)\] \[dist(u) = distance(u)\]

 그런데 이는 처음에 가정했던 $dist(u) > distance(u)$를 만족하지 않으므로, 모순이 발생합니다. 따라서 $u$의 최단경로에는 반드시 $R$ 밖의 점이 하나 이상 존재해야 합니다.

image16

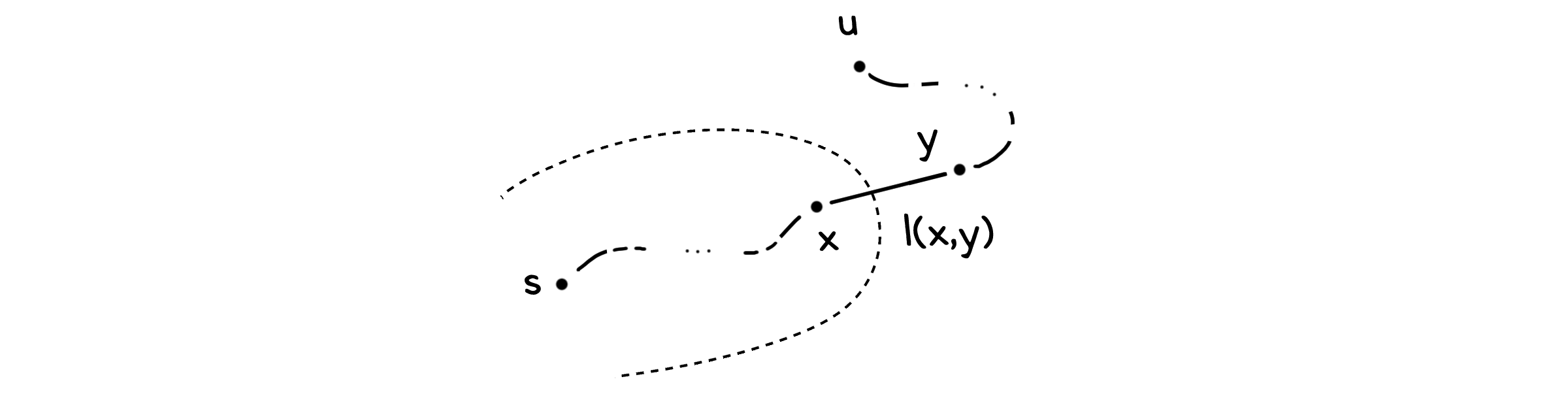
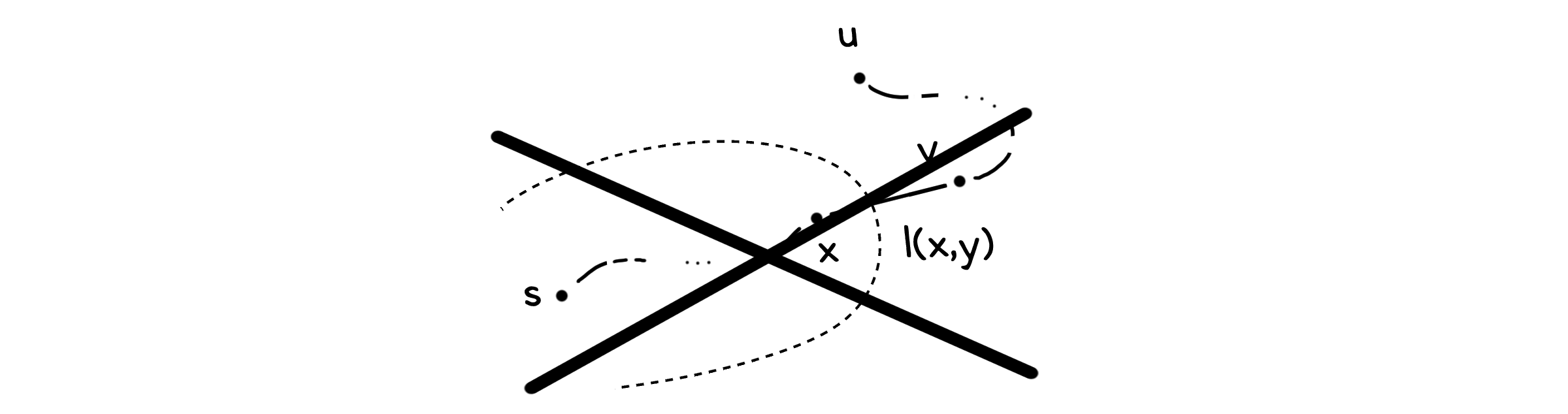
iii) 반증법 - $u$와 $R$ 사이에 점이 존재할 때

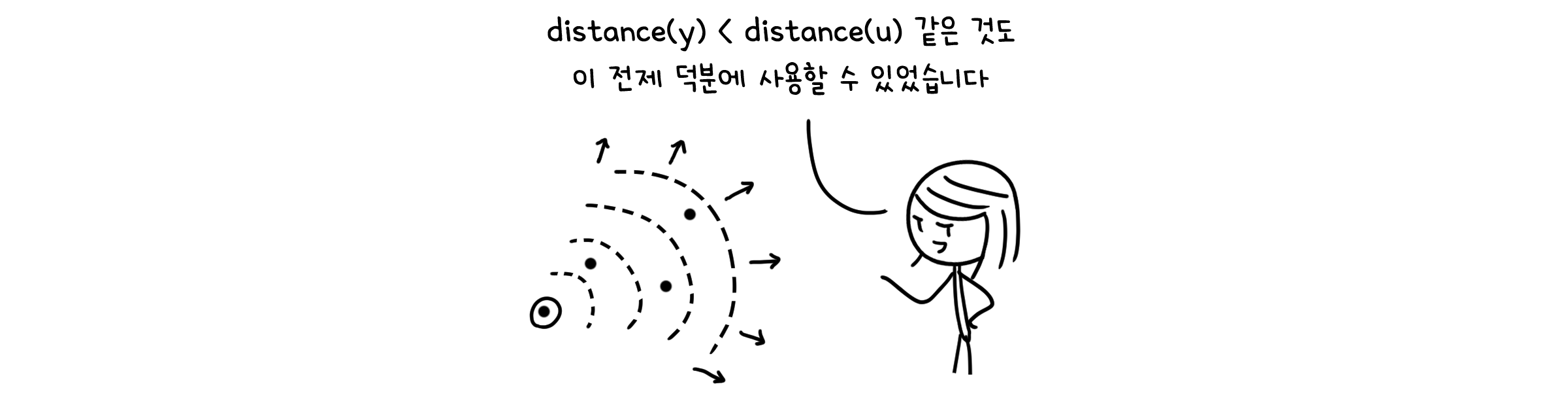
 이제 시작점에서 $u$까지 이르는 실제 최단경로에서 $R$ 바로 앞에 있고 $u$보다 앞서 등장하는 점 $y \in V - R$가 있다고 생각합시다. $y$에게도 바로 이전에 왔던 점 $x \in R$가 있을 테고요.

image17

 $y$는 지금 ii)의 가정중 정확히 $u$와 동일한 상황에 놓여 있습니다. 따라서 이렇게 쓸 수 있습니다.

\[dist(y) = distance(y)\]

 $y$는 $u$보다 앞서 있기 때문에, 다음 부등식을 만족합니다.

\[dist(y) = distance(y) < distance(u) < dist(u) \; \rightarrow \; dist(y) < dist(u)\]

 하지만 알고리즘의 선택 규칙에 의해 $u$는 $R$ 밖의 점 중 $dist$가 최소인 점으로 선택되었습니다. 즉,

\[dist(u) \leq dist(y)\]

 를 만족해야 하는데, 이는 $dist(y) < dist(u)$와 상반되어 모순이 발생합니다.

image18

iv) 결론

 따라서, $R$ 밖에 있는 $u$는 어떠한 경우라도 $dist(u) > distance(u)$를 만족시킬 수 없습니다. $distance$는 실제 최단 길이를 뜻하니까 $dist(u) < distance(u)$ 도 성립할 수 없으므로,

image19

 다익스트라 알고리즘의 정당성을 증명할 수 있습니다.

다익스트라 - 분석

 다익스트라 알고리즘에서 실행시간에 영향을 주는 연산은 delete_min()과 decrease_key(), 그리고 make_queue() 세 가지가 있습니다.

  • delete_min()은 점을 하나 방문할 때마다 호출됩니다. 시작점에서부터 모든 점까지의 거리를 구하기 때문에, $|V|$번 호출됩니다.

  • decrease_key()는 방문한 점과 연결된 모든 점마다 한 번씩 호출됩니다. 이는 모든 선의 수와 같기 때문에, $|E|$번 호출됩니다.

  • make_queue()는 최솟값 큐를 초기화하면서 각 점마다 키값을 집어 넣습니다. 따라서 삽입 작업이 $|V|$번 호출됩니다.

 이 세 가지 함수의 호출 횟수를 종합하면, 다익스트라 알고리즘의 실행시간은

\[O(\|V\| * T(delete_min) + \|E\| * T(decrease_key) + \|V\| * T(make_queue))\]

 라고 둘 수 있습니다. 세 함수의 실행 시간은 따로 명시하지 않았는데, 이는 최솟값 큐가 사용하는 데이터구조에 따라 달라지기 때문입니다. 데이터 구조로 배열(Array)과 이진 힙(Binary Heap)을 사용했을 때, 각각의 알고리즘 실행시간은 이렇게 계산할 수 있습니다.

데이터 구조T(delete_min)T(decrease_key)T(make_queue)실행시간
배열$|V|$11$|V|^2$
이진 힙$\log{|V|}$$\log{|V|}$$\log{|V|}$$(|V|+|E|)\log{|V|}$

허점 - 음의 가중치

 다익스트라 알고리즘의 핵심 원리는 어떤 점의 최단경로는 반드시 그보다 짧은 최단경로를 가지는 점을 거치게 된다는 점입니다. 이는 그래프의 가중치가 모두 양수라는 전제가 있기 때문에 사용할 수 있는 사실입니다.

image20

 그래서 그래프에 음수의 가중치가 존재한다면, 다익스트라 알고리즘은 제 역할을 다할 수 없게 됩니다.

image21

벨만-포드 알고리즘 (Bellman-Ford Algorithm)

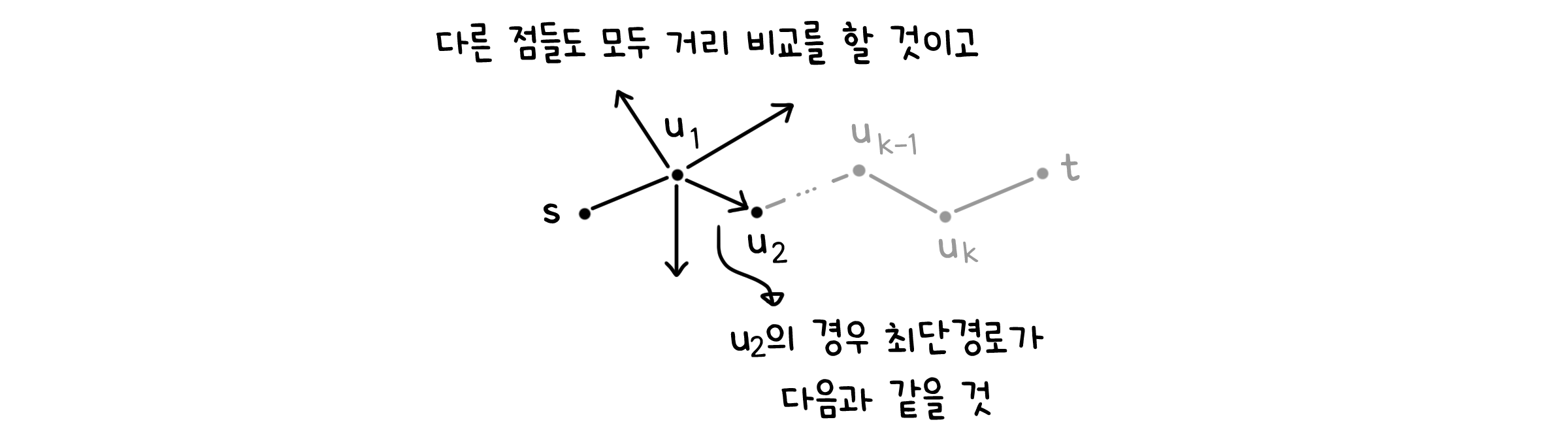
 그렇다면 어떻게 해야 음수 가중치 그래프도 문제 없이 해결할 수 있을까요? 순서를 반대로 해서 생각해봅시다. 어떤 점 $t$에 대해, 이미 그 최단 경로가 정해졌다고 하면 그 경로는 최대 $|V|-1$개의 선을 가질 수 있습니다. 이 선들을 $(s, u_1), (u_1, u_2), … , (u_k, t)$라고 해보죠.

image22

 첫 번째 선 $(s, u_1)$을 제외한 각 선들은 적어도 한 번 $dist(v) = \min { dist(v), dist(u) + l(u, v) }$를 통한 업데이트를 거쳤을 것입니다. $(u_1, u_2)$ 같은 경우 $v = u_2, u = u+1$인 셈입니다. 다만 어디서 $u_1$나 $u_2$가 튀어나올지 모르니까, 단순하게 모든 선에 대해서 $dist(v) = \min { dist(v), dist(u) + l(u, v) }$를 비교해보는 겁니다.

image23

 그리고 이 것을 경로 상의 모든 선들에 대해서 진행할테니, $|V|-1$번 만큼 반복하면 되지 않을까요?

image24

 이 아이디어를 실현한 것이 벨만-포드 알고리즘(Bellman-Ford Algorithm)입니다.

1
2
3
4
5
6
7
8
9
10
11
12
13

# l(u, v) : 점 u와 점 v 사이의 거리
# dist(x) : 시작점으로부터 점 x 까지의 최단거리
# prev(x) : 최단경로 상 점 x의 이전 점

def Bellman_Ford(G=(E,V): Graph, s: Vertex):
  for u in V:
    dist(u) = infinite  # 처음엔 어떠한 점도 방문하지 않음
    prev(v) = None

  dist(s) = 0  # 시작점은 거리 0
  for i := 1 to |V|-1:  # 시작점을 제외하고 점의 개수만큼 반복
    for e=(u, v) in E:  # 모든 선에 대해
      dist(v) = min(dist(v), dist(u) + l(u, v))  # 길이 갱신

image25

벨만-포드 - 분석

 항상 최소 길이를 가지는 점을 선택하는 다익스트라 알고리즘과 달리, 벨만-포드 알고리즘은 항상 모든 선에 대해 길이를 갱신합니다. 그래서 놓치는 예외 없이(심지어 음의 가중치 까지도) 최적의 경로를 알아낼 수 있는 것이죠. 단점이라고 한다면, 매번 모든 선을 갱신하기 때문에 실행시간이 늘어난다는 것 정도 입니다. 전체 $|V|-1$번 호출 마다 모든 선 $|E|$개에 대해 길이를 갱신하기 때문에, 전체 실행 시간은 $O(|V||E|)$ 가 됩니다. $O(|V|) < |E| < O(|V|^2)$인 것을 감안하면, 상당히 시간이 걸린다는 것을 짐작할 수 있습니다.

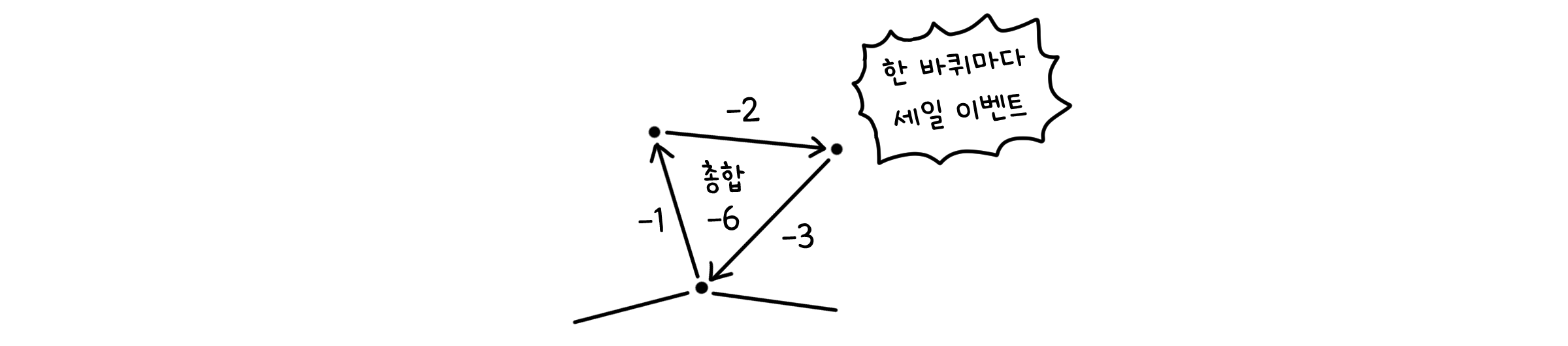
허점 - 음의 순환

 벨만-포드 알고리즘에도 문제점은 남아 있습니다. 만약 가중치의 총합이 양수가 아닌 순환이 존재한다면, 최단경로는 영원히 순환 안을 돌게된다는 것입니다. 한 바퀴를 돌 때마다 길이가 길어지기는 커녕 오히려 짧아지게 되니까요. 몇 번이고 돌지 않을 이유가 없죠.

image26

 사실 이건 벨만-포드 알고리즘의 문제라기 보다는 그래프 자체의 허점이기 때문에, 알고리즘 쪽에서 취할 수 있는 방법이 딱히 없습니다. 하지만 적어도 그래프에 음의 순환이 있다는 것을 판단하게 만들 수는 있겠죠. 음의 순환이 있다면 최단 경로는 끝없이 줄어들테니, $|V|-1$번의 반복을 끝낸 후에도 최단 경로는 갱신될 수 있습니다. 따라서 우리는 한 번의 반복을 더 수행합니다.

1
2
3
4
5
6
7
8

def Bellman_Ford(G=(E,V): Graph, s: Vertex):
  # ...
  for i := 1 to |V|-1:
    # ...

  for e=(u, v) in E:
    if dist(v) < dist(u) + l(u, v):  # 만약 갱신되는 길이가 있다면
      return "negative cycle exists"  # 음의 순환이 존재함

 만약 거기서도 길이가 줄어드는 경로가 생긴다면, 끝없이 돌아가는 음의 순환이 존재한다는 뜻이니까요.

image27

cm301
알고리즘
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.