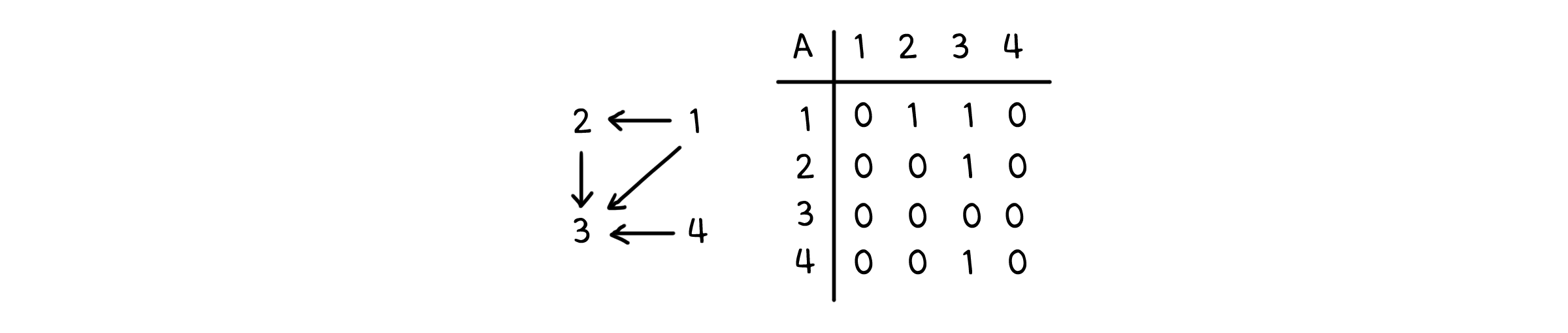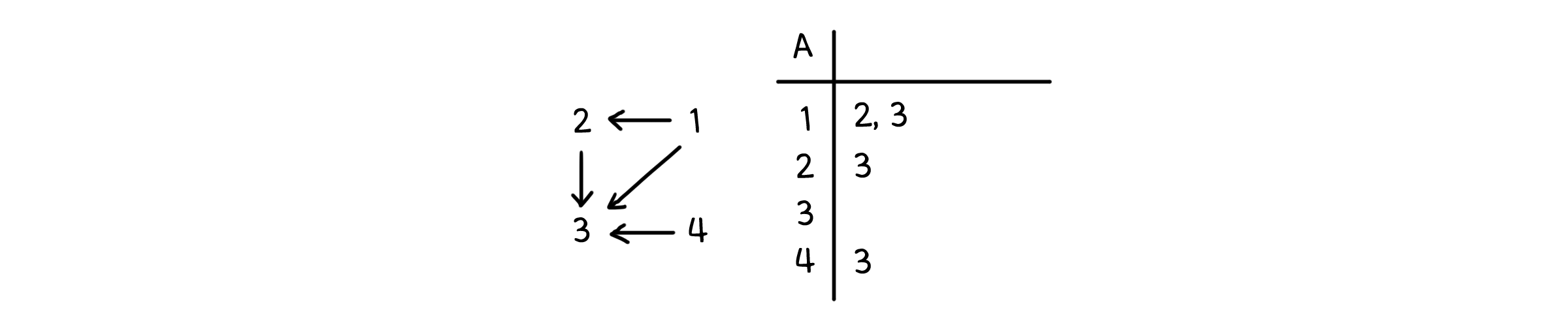[CM301] 06. 그래프 (Graph)
세상에 우리를 괴롭히는 문제들은 공통점이 있습니다. 복잡하고 더럽게 꼬여 있다는 것이죠.
알고리즘에서 다루는 문제들도 별반 다르지 않습니다. 보통 복잡한 문제들은 여러 요인들이 수많은 관계를 가지고 엮여 있기 때문에, 당최 한 가지만 생각할 수 없는 경우가 부지기수를 이룹니다. 이럴 때 우리에게 필요한 것은 - 그래프입니다.
문제의 대다수는 그래프로 표현할 수 있습니다.
그래프 (Graph)
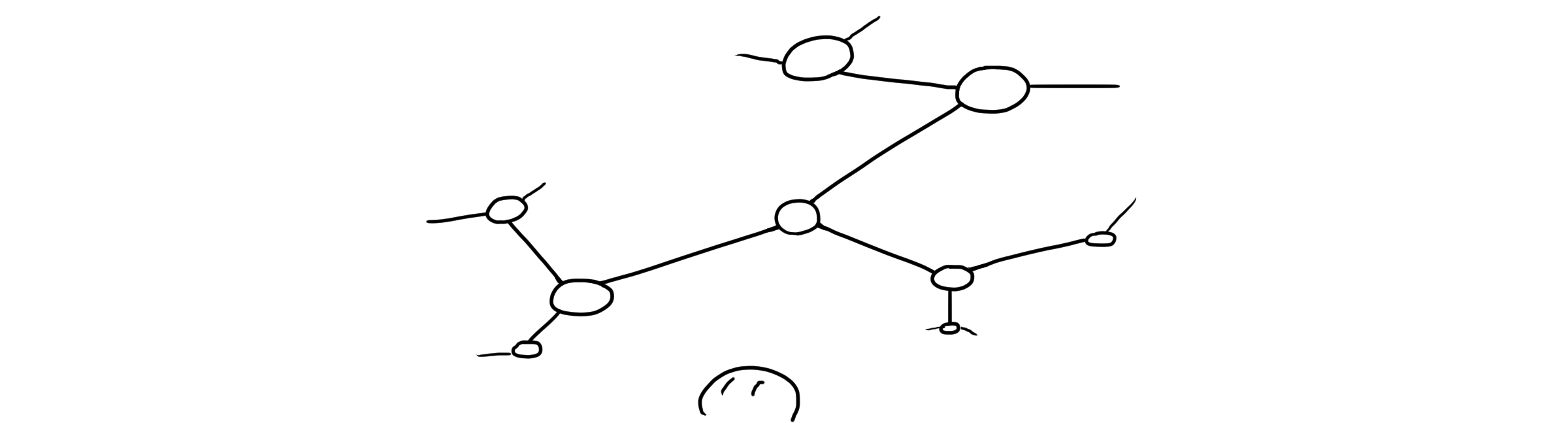
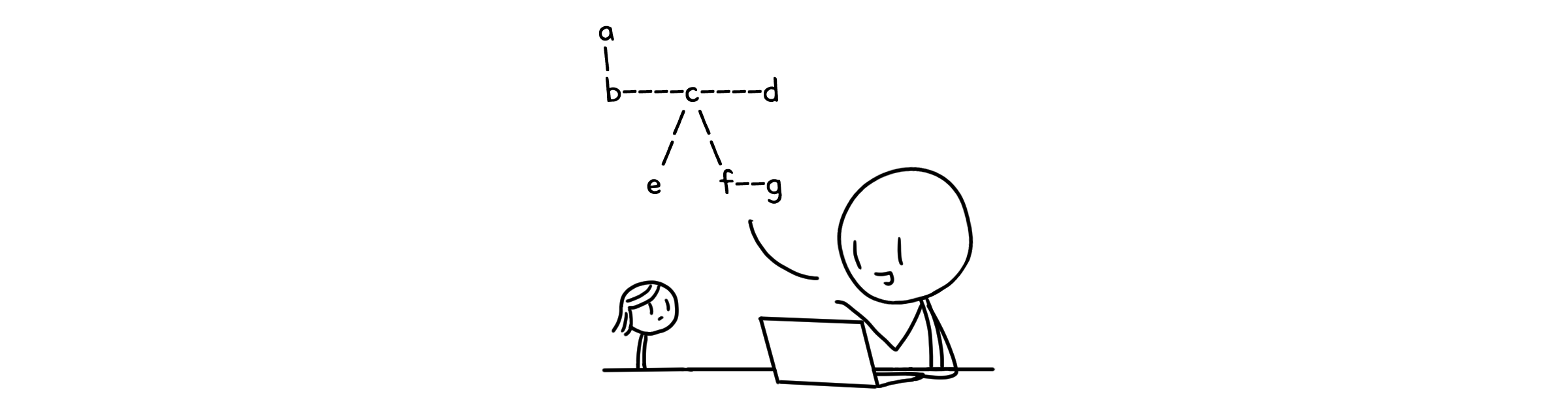
수학적으로 정의되는 그래프는 점과 선의 집합입니다. x축, y축, 단위 이런 것들 필요 없이 정말 점과 선만 있으면 돼요. 좀 더 엄밀하게 표현해봅시다. 점(Vertex, 또는 Node)들의 집합 $V$와 그 점들을 잇는 선(Edge)들의 집합 $E$가 있을 때, 그래프 $G$를 다음과 같이 정의할 수 있습니다.
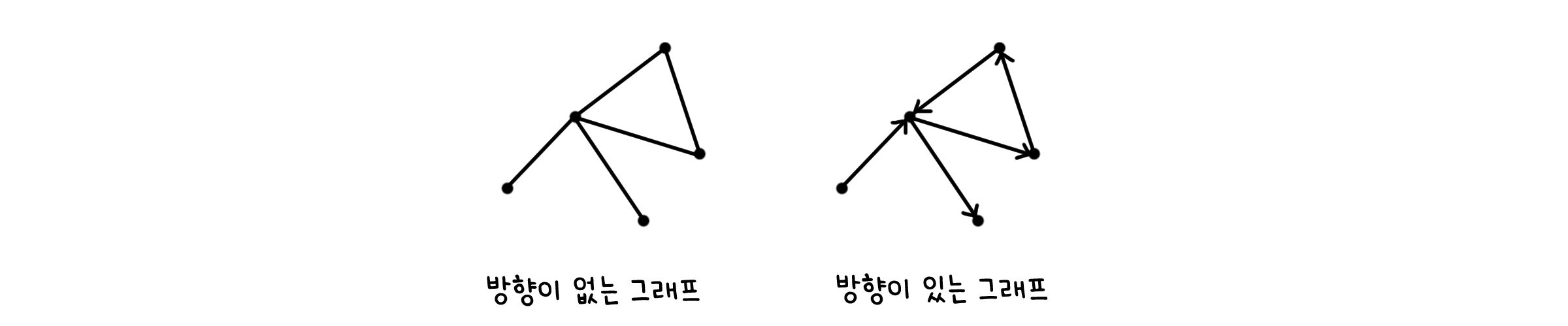
\[G = (V, E)\]선으로 연결되는 방법은 두 가지가 있습니다. 방향이 없어 두 점의 순서와 관계 없이 선으로 연결되어 있다고 말할 수 있으면 방향이 없는 그래프(Undirected graph)라고 합니다. 반대로, 방향이 있어 어떤 점이 처음에 오느냐에 따라 연결 여부가 달라진다면 방향이 있는 그래프(Directed graph)라고 합니다.
이 포스트는 그래프 알고리즘을 이해하는데 필요한 기본 개념만 설명하였습니다. 그래프와 관련된 다른 내용은 ‘이산구조’ 포스트에서 더 자세히 다루었으니, 살펴보기 바랍니다.
연결된 그래프
만약 모든 점들이 어떻게든 서로 연결되어 어떤 두 점을 잡아도 서로 연결되는 경로(Path)가 존재한다면, 그 그래프는 연결되어 있다(Connected)고 말합니다.
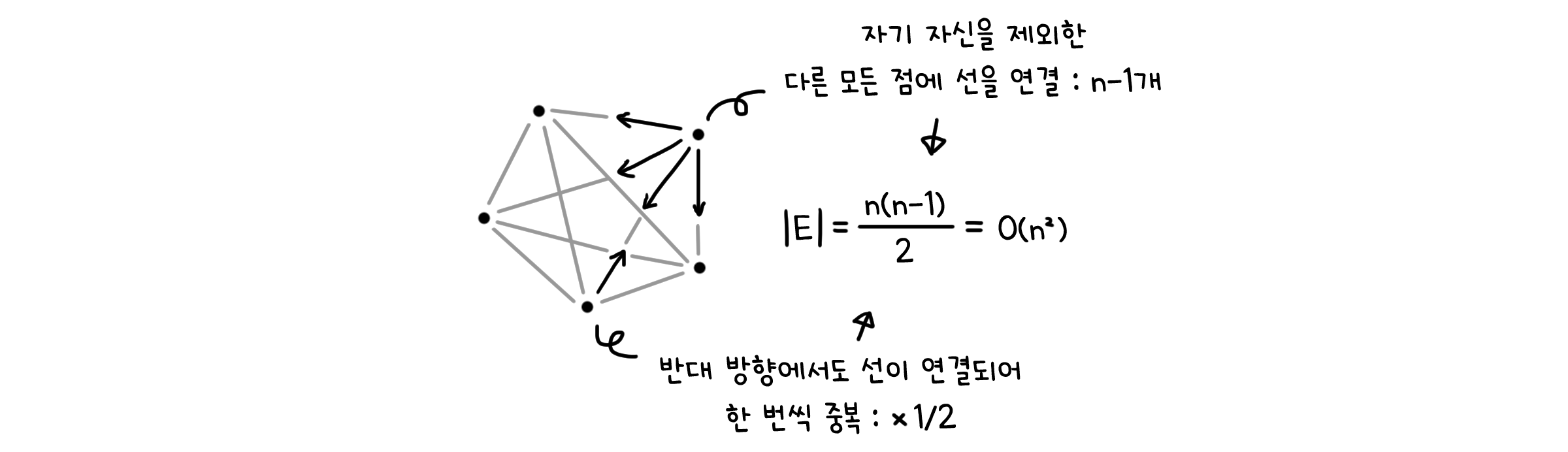
연결된 선의 개수에 따라, 그래프가 연결된 정도를 구분할 수 있습니다. 선을 최소한으로 사용한다면 $|V| - 1$개의 선만으로도 그래프를 연결할 수 있습니다. 반대로 선을 최대로 사용하면 $|V|^2$에 비례하는 선, 즉 $O(|V|^2)$ 만큼의 선이 필요할 것입니다. 깊게 생각할 필요 없이 학교에서 배웠던 대각선의 개수 구하는 방법을 살펴보면 알 수 있죠.
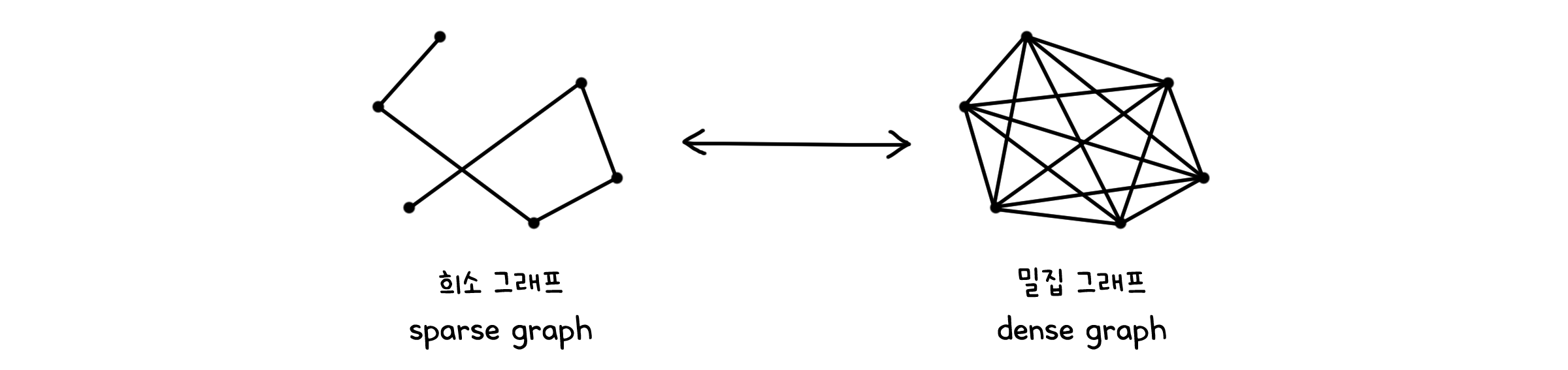
아무튼 연결된 그래프는 $|V| - 1$과 $O(|V|^2)$ 사이의 개수만큼 선을 가지게 될 것입니다. $|V| - 1$개에 가까워질수록 그래프는 희소(Sparse)하게 되며, $O(|V|^2)$개에 가까워질수록 밀집(Dense)하게 됩니다.
그래프를 행렬로 표기하기
이제 그래프가 무엇인지 알았으니, 알고리즘에 써 먹어야겠죠. 얼핏 보면 점과 선으로 이루어진 그림이니, 그래프 모양 그대로 컴퓨터 안에 집어 넣는 것은 아무래도 무리가 있습니다.
그래서 우리는 그래프가 점들 사이의 관계를 나타낸다는 사실을 이용합니다. 선으로 연결되어 있다면 그래프 관계에 있는 것이고, 그렇지 않다면 관계에 있지 않은 것이죠.
인접행렬 (Adjacency Matrix)
가장 간단한 방법은 두 점을 순서쌍으로 두어, 점들이 선으로 연결되어 있는지에 따라 값을 정하는 것입니다.
\[A[i,j] = \begin{cases} 1 & (i,j) \in E \; \text{일 때} \\ 0 & (i,j) \notin E \; \text{일 때} \end{cases}\]행렬을 사용하면 이 방법을 쉽게 구현할 수 있습니다. 행과 열의 인덱스를 각각의 점으로 두고, 원소는 0 또는 1로 채우면 되거든요. 이를 인접 행렬(Adjacency Matrix)라고 부릅니다. 인접 행렬은 점의 개수가 $V$개 일 때 $V * V$ 크기의 정사각 행렬이 되기 때문에, 항상 $\Theta(V^2)$의 크기를 사용합니다.
인접 리스트 (Adjacency List)
모든 순서쌍 값을 저장하는 대신, 선으로 연결된 점들만 따로 저장하면 공간을 절약할 수 있습니다. 하나의 점에 대해, 그 점과 선으로 연결되어 있는 점들이 무엇인지 나열하는 방식으로요.
\[\begin{aligned} \mathrm{Adj}[1] &= \{2, 3\} \\ \mathrm{Adj}[2] &= \{3\} \\ \mathrm{Adj}[3] &= \{\} \\ \mathrm{Adj}[4] &= \{3\} \end{aligned}\]이 방법에 사용할 수 있는 구조는 리스트입니다. 리스트의 각 인덱스를 점으로 두고, 각 원소는 그 점과 연결되어 있는 점들의 집합으로 두면 됩니다. 이를 인접 리스트(Adjacency List)라고 부릅니다. 점의 개수가 $V$, 선의 개수가 $E$일 때, 인접 리스트는 $V$의 길이를 가집니다. 그리고 원소가 되는 집합을 모두 합친 크기는 $E$ 만큼이 됩니다(만약 방향이 없는 그래프라면 양방향 모두 포함되니 $2E$가 됩니다). 따라서 인접 리스트는 항상 $\Theta(V+E)$의 크기를 사용합니다.
방향이 있는 그래프
그래프는 관계를 나타내는 방식입니다. 다른 종류의 관계를 나타내기 위해서는 그에 맞는 모양의 그래프가 필요하죠.
방향이 있는 비순환 그래프 (Directed Acyclic Graph, DAG)
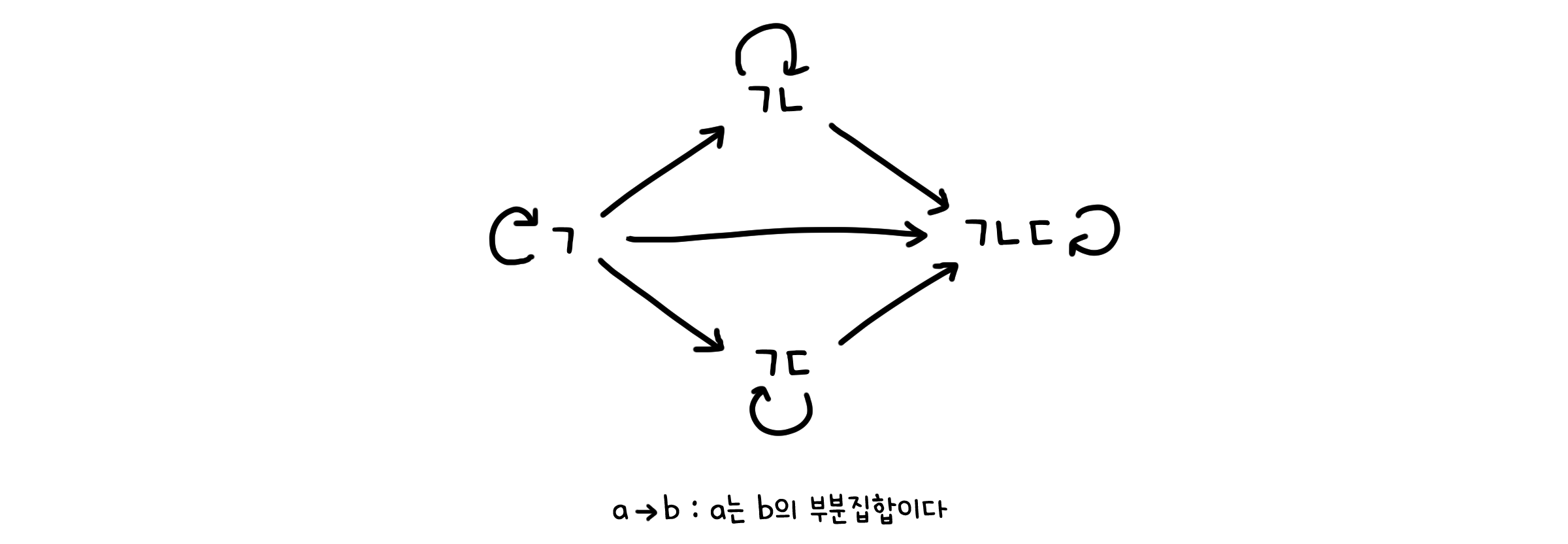
예를 들어 봅시다. 요소들이 아래 조건들을 만족하면 부분 순서(Partial Order)의 관계라고 합니다.
반사적(Reflective) : 자기자신과의 관계가 속할 것 ($(x, x) \in R$)
비대칭적(Asymmetric) : 어떤 관계의 반대는 속하지 않을 것 ($(x, y) \in R \rightarrow (y,x) \notin R$)
추이적(Transitive) : 순서 관계가 일관적일 것 ($(x, y) \in R and (y, z) \in R \rightarrow (x, z) \in R$)
부분순서를 비롯한 다른 순서에 대해서는 ‘이산구조’ 포스트에서 더 자세히 다루었으니, 살펴보기 바랍니다.
이 조건을 만족하면서 부분 순서 관계를 그래프로 나타내기 위해서는 두 가지 조건이 필요합니다.
비대칭적이기 위해서, 선은 방향이 있어야 합니다. 방향이 없다면, 양방향의 순서쌍 모두 관계에 포함될 것입니다.
추이적이기 위해서, 그래프는 순환하지 않아야 합니다. 순환한다면 마지막 노드가 첫 노드 전에 위치하는 모순이 발생합니다.
따라서, 부분 순서를 나타내는 그래프는 방향이 있는 비순환 그래프(Directed Acyclic Graph, DAG)가 되어야 합니다.
위상정렬 (Topological Sort)
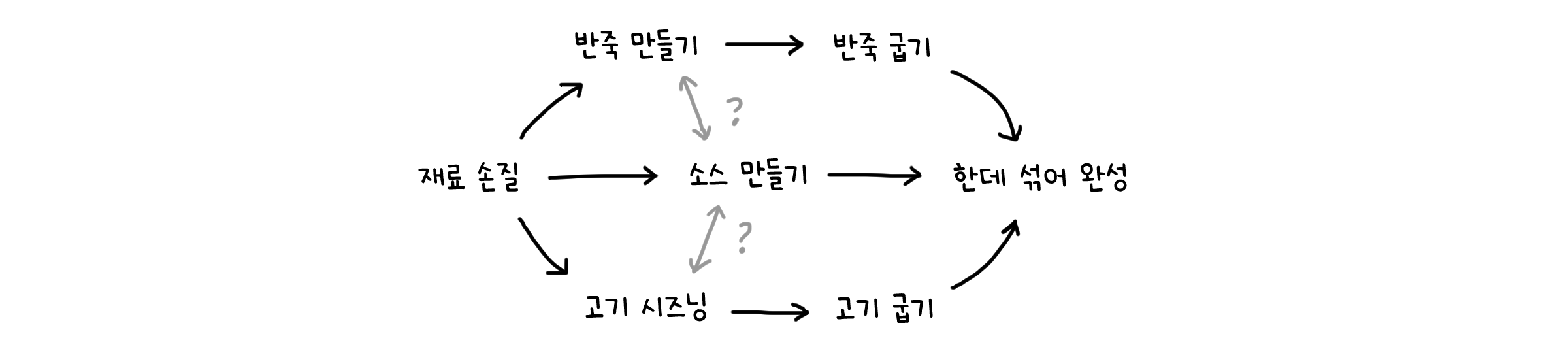
DAG는 순환이 없기 때문에, 작업 절차나 교육과정의 선수과목처럼 순서가 있는 상황을 표현할 수 있습니다. 하지만 DAG로 표현 가능한 순서는 부분순서로, 모든 요소들이 순서 관계를 가지는 것은 아닙니다.
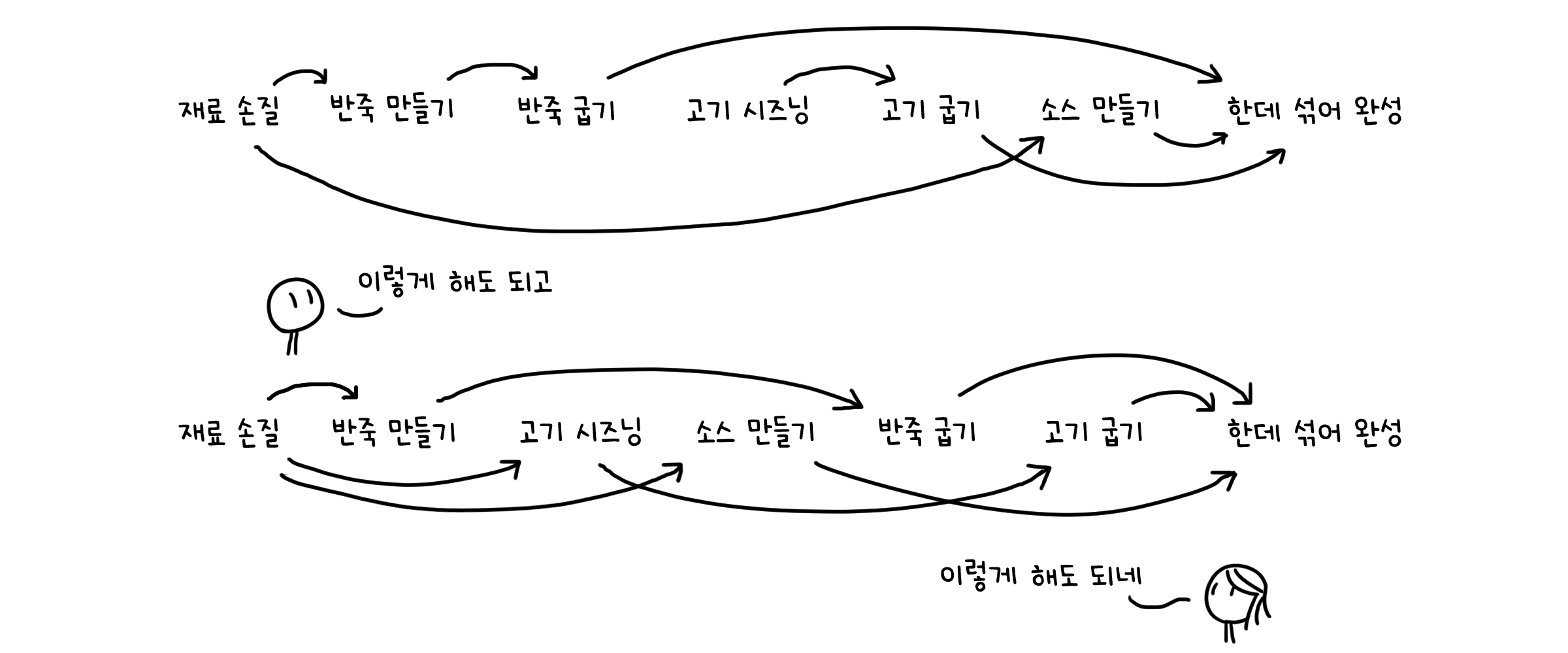
그렇기 때문에 DAG로 표현한 그래프의 점들을 일렬로 정렬할 때는 한 가지 규칙을 정합니다. 어떤 두 점 $u, v$가 $(u, v) \in E$로 이어져 있다면, 정렬할 때 $u$가 $v$보다 먼저 나오기만 하면 된다는 것입니다. 이 하나의 간단한 규칙에 따라 점들을 일렬로 정렬하는 것을 위상 정렬(Topological Sort)라고 합니다.
물론, 이 규칙을 따르면 하나의 DAG에서 여러 종류의 정렬이 나올 수 있습니다.
방향이 있는 순환 그래프 (Directed Cyclic Graph)
그런데… 현실의 방향 그래프는 대부분 사이클을 가집니다. 이럴 땐 어떻게 해야 할까요?
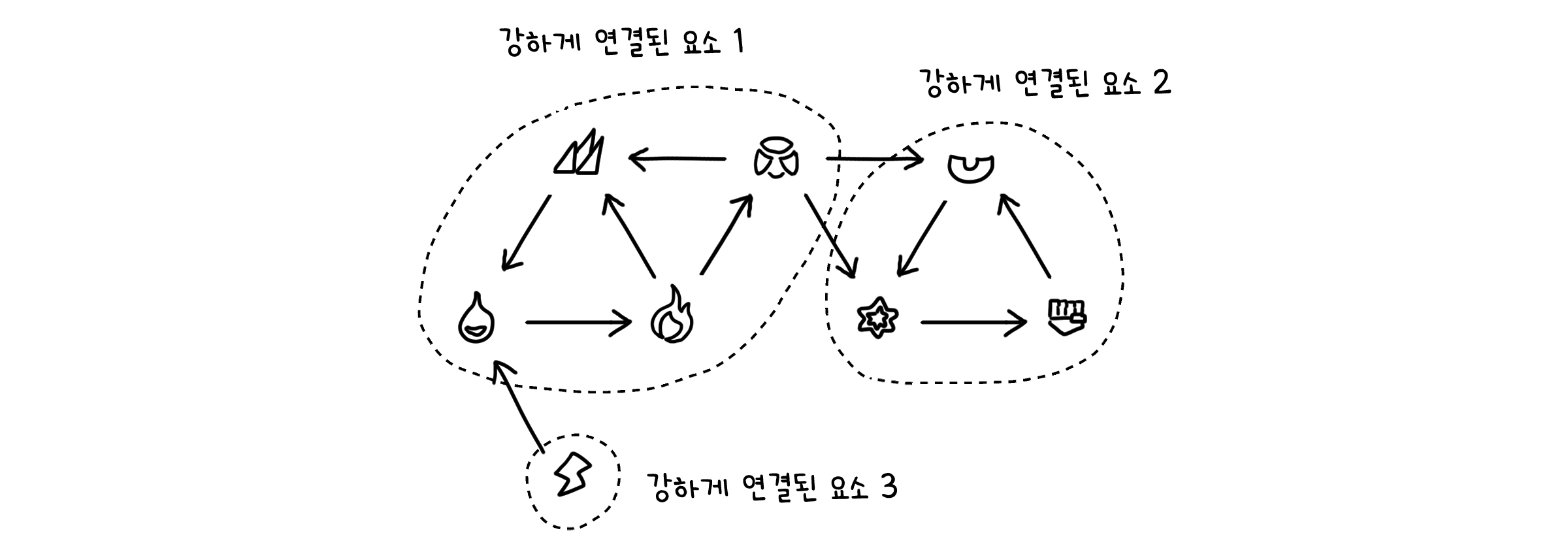
순환이 존재하는 요소들 사이에는 순서가 성립할 수 없습니다. 꼬리에 꼬리를 무는 모양이니까요. 때문에 이들은 한데 묶어 하나의 요소로 생각합니다. 이렇게 양방향으로 도달할 수 있는 점들을 최대한 많이 모은 묶음을 강한 연결 요소(Strongly Connected Component, SCC)라고 합니다.
방향이 있는 순환 그래프에서 SCC들을 찾아 하나의 점으로 압축한다면, 그래프는 DAG가 될 수 있습니다. 순서를 세울 수 있게 되는 것이죠.
그렇다면 중요한 것은 그래프가 순환하는지 판단하고, 순환한다면 SCC가 무엇인지 알아내는 것 입니다. 간단한 그래프라면 빙빙 도는 모양을 쉽게 찾아낼 수 있을 것입니다. 하지만 점과 선들이 점점 많아진다면…?
쉽지 않겠죠. 이제 알고리즘을 사용할 때입니다…
깊이 우선 탐색 (Depth First Search, DFS)
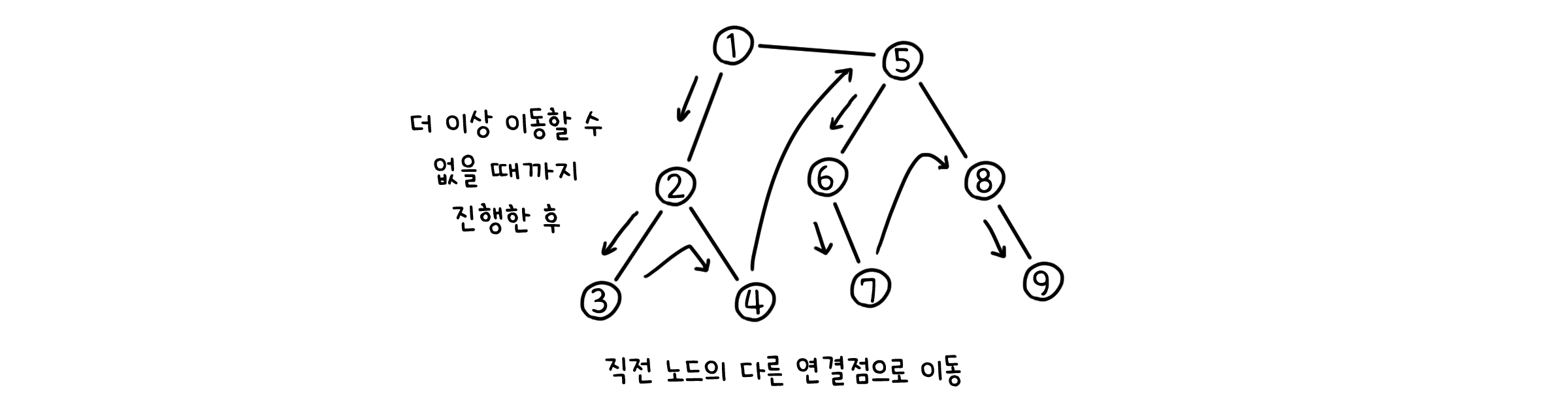
깊이 우선 탐색(Depth First Search, DFS)은 그래프의 경로, 즉 깊이를 먼저 늘리는 방향으로 탐색하는 그래프 탐색 방법입니다.
작성된 모든 코드는 Python의 형식을 빌린 유사 코드이며, 문법을 다소 무시한 부분이 있기 때문에 실행이 되지 않습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def DFS(G=(E,V): Graph):
for v in V:
visited(v) = false # 처음엔 어떤 노드도 방문하지 않았음
for v in V: # 모든 점에 대해
if not visited(v): # 방문하지 않았다면
Explore(v) # 탐색을 실행
def Explore(v: Vertex):
visited(v) = true # 탐색을 시작하는 노드를 방문 처리
for u := (v, u) in E: # v와 연결된 모든 점 u에 대해
if not visited(u) # u를 아직 방문하지 않았다면
Explore(u) # u 탐색을 실행
DFS - 정당성
위 알고리즘이 정말 모든 점들을 탐색할 수 있는지, 그 정당성을 증명해봅시다.
반증법으로 접근합니다. 만약 DFS를 실행했음에도 미처 방문하지 못한 점 $u$가 남았다고 가정합시다. 우리가 DFS를 시작한 점을 $v$라고 하면 $v$에서 $u$까지 이어진 경로가 있을 것입니다.
이 경로를 따라 Explore() 함수가 탐색을 진행했을 때, 마지막으로 방문한 점을 $z$라고 합시다. $z$는 $u$의 이전에 있을 것입니다.
만약 $z$ 바로 다음에 $w$라는 점이 있다고 합시다. $z$가 마지막으로 방문한 점이므로, $w$ 또한 방문하지 못한 점입니다. 그런데 DFS의 정의에 따르면, DFS가 $z$를 방문할 때 $z$와 인접한 모든 점에 대해 Explore()를 실행합니다. 거기에 $w$도 포함되니, ‘$w$는 방문하지 않는다’라는 사실은 모순이 됩니다.
따라서, DFS는 모든 점을 방문할 수 있습니다. $\Box$
DFS - 분석
노드를 방문했는지 판단할 수 있는 visited 리스트를 둔 덕분에, DFS를 하는 동안 중복 방문을 피할 수 있습니다. 때문에 Explore()는 각 점마다 한 번씩, 총 $|V|$번 호출됩니다.
1
2
3
4
5
6
def Explore(v: Vertex):
visited(v) = true # visited() 호출
for u := (v, u) in E:
if not visited(u) # 중복 방문 방지
Explore(u)
한 점 $v$를 방문했을 때, Explore()는 그 점과 연결된 점들을 찾기 위해 반복문을 실행합니다. 이때 연결된 점들은 $v$와 연결된 선의 개수 만큼 존재합니다. 따라서 모든 점들을 순회했을 때 반복문은 총 $2|E|$번(방향이 없을 때) 또는 $|E|$번(방향이 있을 때) 실행될 것입니다.
1
2
3
4
def Explore(v: Vertex):
# ...
for u := (v, u) in E: # v와 연결된 모든 점 u의 개수만큼 반복
# ...
따라서 DFS의 실행시간은 $O(|E|+|V|)$이 됩니다.
DFS는 모든 점을 순회합니다. 따라서, 요소를 탐색하는데 DFS를 사용한다면 반드시 탐색을 완료할 수 있습니다.
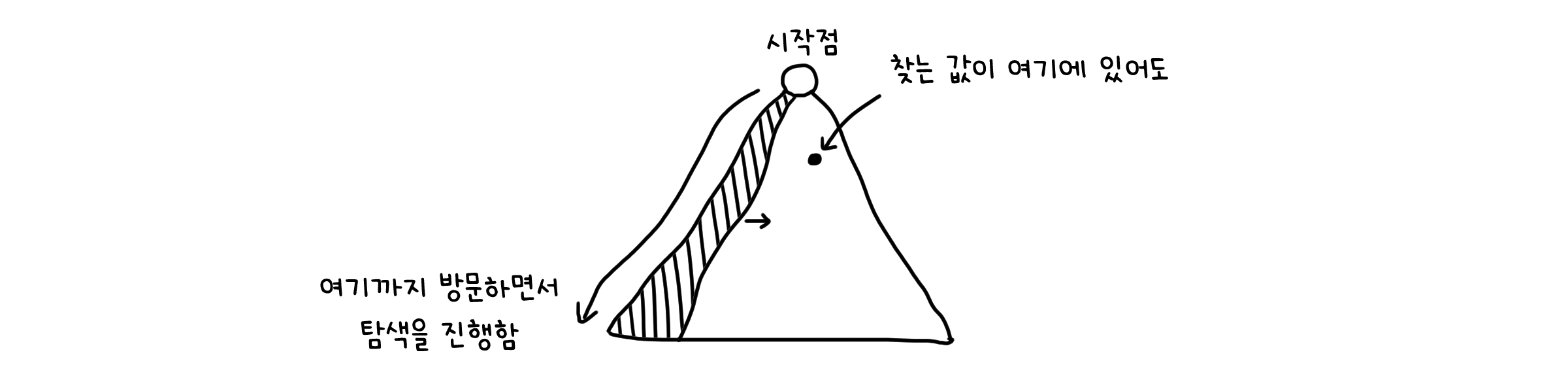
하지만, 탐색을 빠르게 해내는 것은 아닙니다. DFS는 깊이를 우선으로 해서 탐색을 진행합니다. 그래서 원하는 값이 시작점과 가까이 있어도 다른 노드를 선택한다면, 다시 시작점으로 돌아오기까지 꽤나 많은 시간이 걸릴 것입니다.
DFS의 변칙들
한계가 있는 깊이 우선 탐색 (Depth-limited Search)
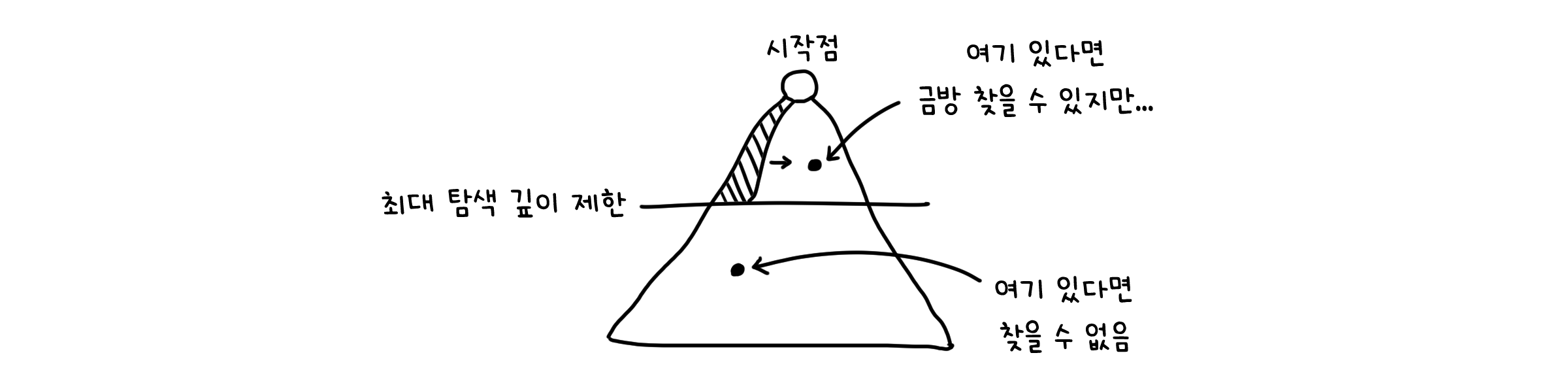
빠른 탐색이 힘든 DFS의 단점을 해결하기 위해, 탐색하는 깊이에 제한을 두는 방법입니다. ‘여기까지 가도 안 나오니까 그만 가고 길을 바꾸자’인 셈이죠. 사용자가 설정한 최대 깊이에 따라 알고리즘의 실행시간도 조절할 수 있다는 장점이 있습니다. 하지만, 찾고자 하는 값이 설정한 깊이보다 더 깊이 있다면 탐색이 불가능하다는 다소 치명적인 단점이 있습니다.
반복적 깊이 탐색 (Iterative deepening search)
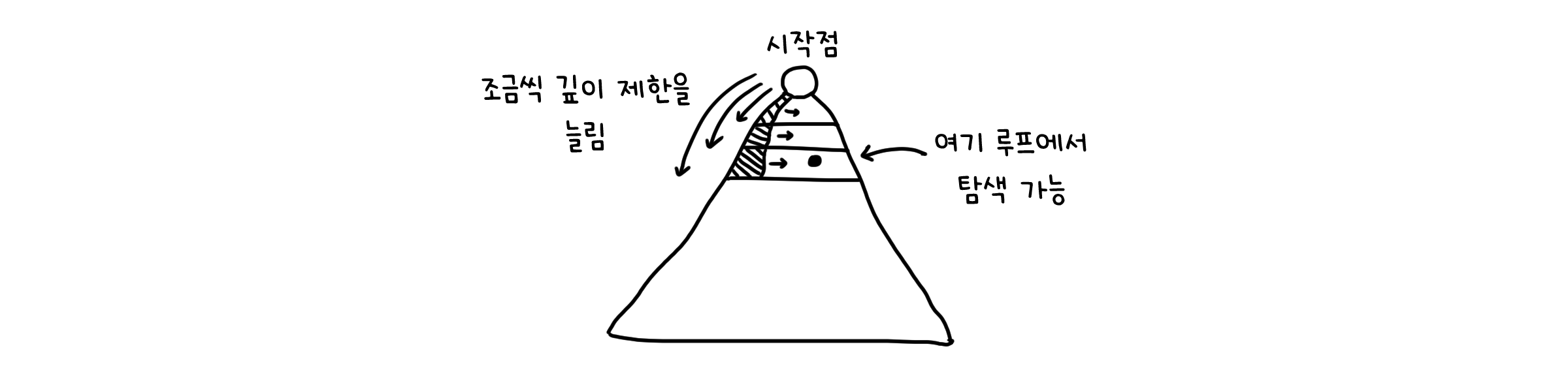
위 버전의 DFS의 문제를 개선한 방법이 반복적 깊이 탐색입니다. 마찬가지로 최대 탐색 깊이를 정해놓은 대신, 최대 탐색 깊이를 조금씩 늘려가며 DFS를 반복하기 때문에 원하는 요소를 찾을 수 있게 되었습니다. 물론 요소를 찾을 때 까지 반복을 이어가기 때문에, 찾고자 하는 값이 제일 끝에 있다면 실행시간이 늘어날 수 있다는 단점이 존재합니다.
DFS로 SCC 찾기
DFS에 대해 살펴보기 전, 우리는 방향이 있는 순환 그래프에서 SCC를 찾는 방법에 대해 이야기 하고 있었습니다. DFS를 알아본 이유는, DFS를 이용하면 SCC를 찾을 수 있기 때문이겠죠! 하지만 DFS를 이용한 알고리즘을 소개하기 앞서 먼저 알아야 할 개념이 몇 가지 있습니다.
실행시각 측정하기
일단 그래프의 각 점마다 Explore() 함수를 실행하는 시각과 종료하는 시각을 측정해야 합니다.
물론 진짜 시계로 직접 측정하는 것은 아니고요, DFS를 진행하는 동안 방문했던 노드 수를 기준으로 삼을 것입니다. 어쨌거나 노드를 많이 방문할수록 걸리는 시간도 길어질테니까요. 점과 점 사이의 상대적인 시간 차이만 알면 됩니다. 이를 위해 Explore() 함수 밖에서 전역으로 사용할 변수 clock이 필요합니다.
1
clock = 0 # 실행시각과 종료시각을 측정할 변수
그리고 각각의 점에게는 실행시각과 종료시각을 저장할 공간 previsit과 postvisit이 필요합니다. clock은 Explore()가 시작할 때 한 번 증가하고, 또 종료되기 전에 한 번 증가합니다. 이 증가한 두 수가 실행시각과 종료시각이 되고, 각각 previsit과 postvisit에 저장될 것입니다.
1
2
3
4
5
6
7
8
9
10
11
12
def Explore(v: Vertex):
clock += 1 # 실행시각
x.previsit = clock # previsit에 저장
visited(v) = true
for u := (v, u) in E:
if not visited(u)
Explore(u)
clock += 1 # 종료시각
x.postvisit = clock # postvisit에 저장
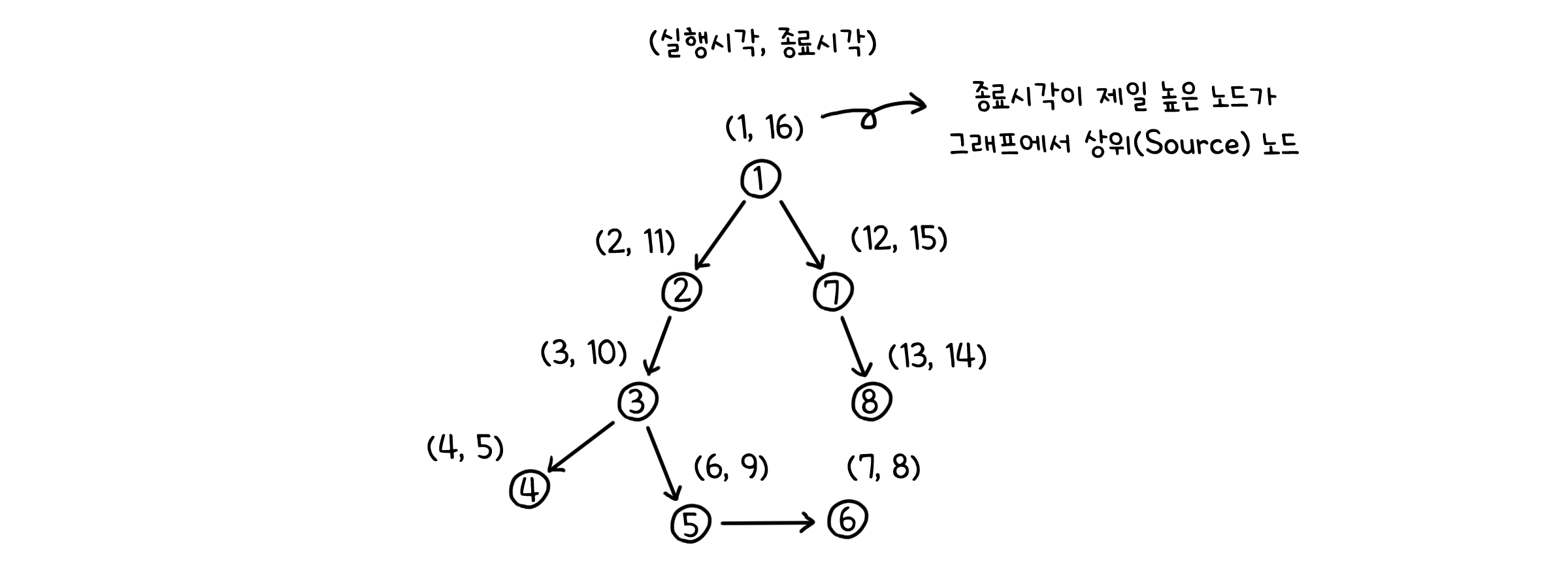
이렇게 하면 각 노드에서 언제 탐색을 시작하고 언제 탐색을 종료하는지 알 수 있습니다. 기억해야 할 것은, 종료시각이 늦은 노드일 수록 위상 정렬에서 순서가 앞에 오게 된다는 것입니다. 만약 종료시각이 제일 늦은 노드가 있다면, 그 노드는 그래프에서 최상위에 있는 노드(Source node)가 됩니다.
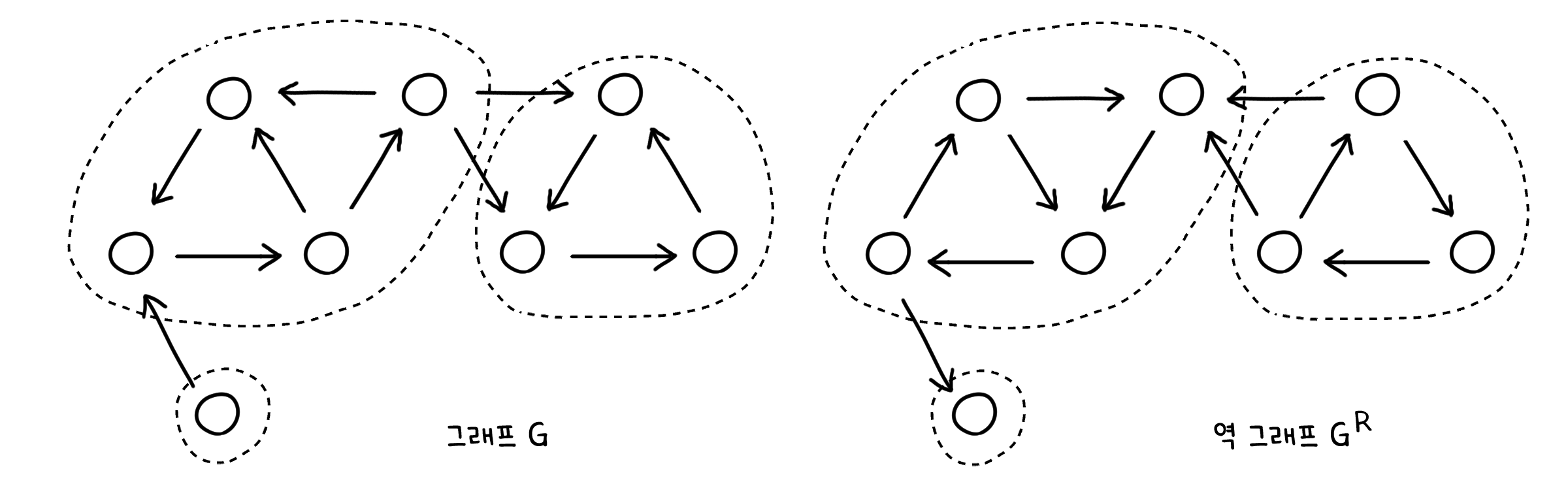
역 그래프 (Reverse Graph)
역 그래프(Reverse Graph)는 방향이 있는 선의 방향을 모두 반대로 뒤집은 그래프입니다. 원래 그래프가 $G$일 때, 역 그래프는 $G^R$로 표기합니다.
역 그래프에서 가장 중요한 점은, 그래프가 뒤집혀도 SCC는 변하지 않고 남아 있다는 것입니다. 이 특징은 다음에 나올 알고리즘에서 요긴하게 사용됩니다.
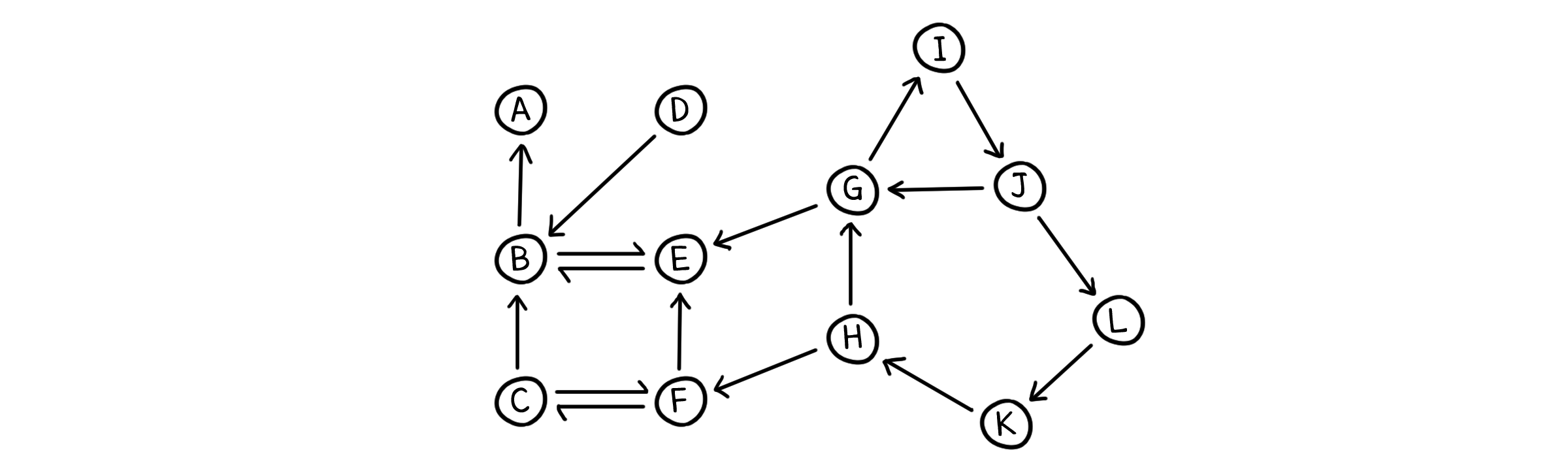
코사라주 알고리즘 (Kosaraju’s Algorithm)
삼바시바 라오 코사라주(S. Rao Kosaraju) 컴퓨터 과학 교수가 고안한 이 알고리즘은 방향이 있는 그래프에서 DFS를 이용해 SCC를 찾아낼 수 있습니다. 코사라주 알고리즘은 아래 간단한 세 가지 단계로 이루어져 있습니다.
주어진 그래프 $G$에서 DFS를 수행한다. 이 때, 실행 시간을 기록한다.
주어진 그래프를 뒤집은 역 그래프 $G^R$를 만든다.
노드마다 종료시간이 가장 늦은 순서대로 DFS를 실행한다. 각 노드마다 탐색이 종료되기 까지 방문한 노드들이 SCC가 된다.
굉장히 간단한 알고리즘인데, 이것이 정말 SCC를 찾아낼 수 있는지 증명하기 위해 예시를 통해 과정을 살펴봅시다.
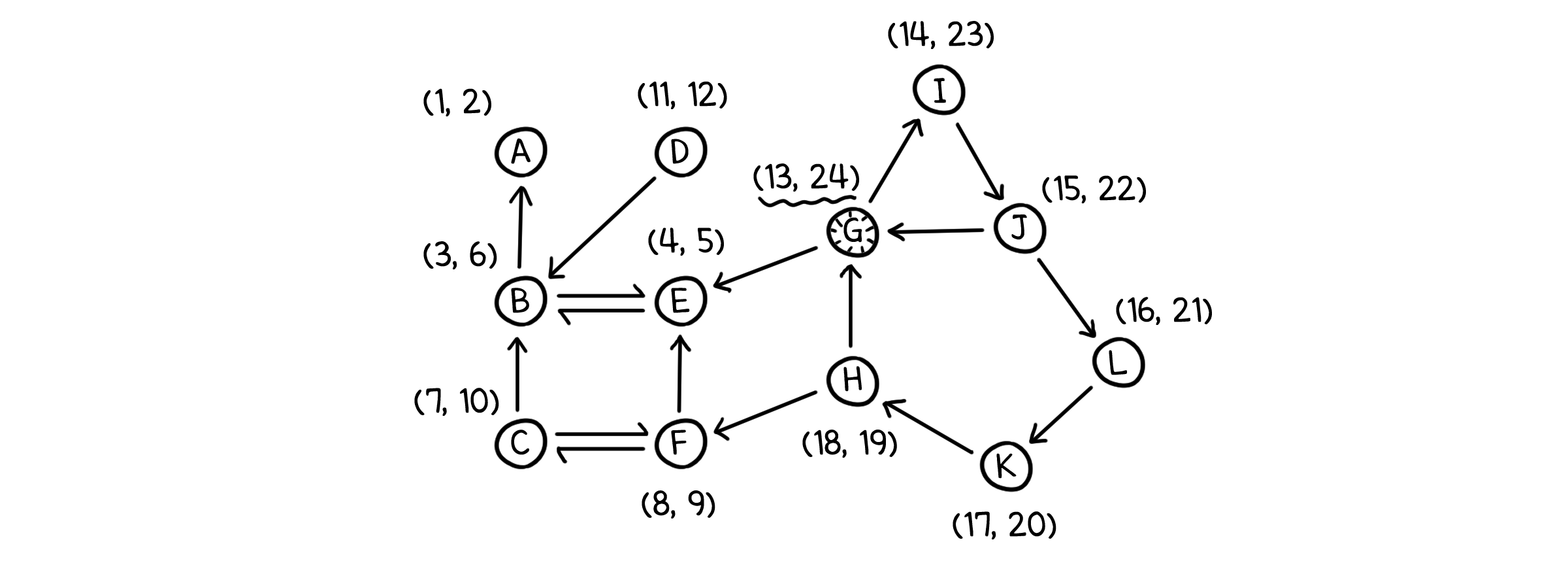
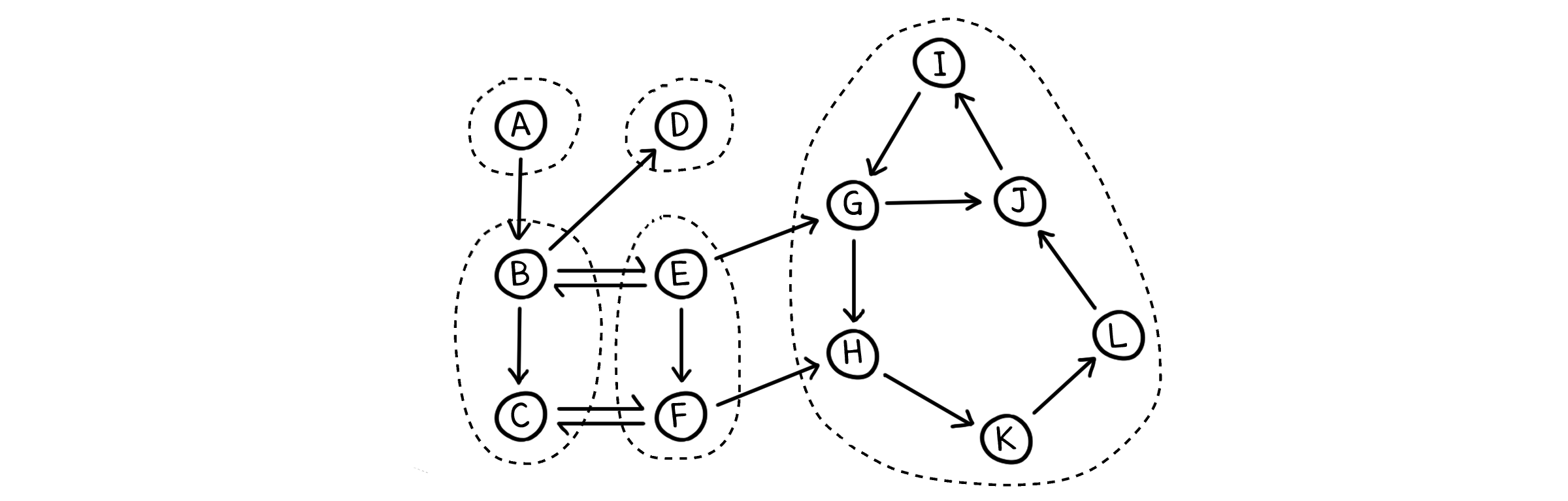
먼저 DFS를 진행하면 실행시각과 종료시각을 얻을 수 있습니다. 종료시각이 제일 늦은 노드는 G입니다. G가 포함된 SCC는 최상위 노드가 될 것입니다.
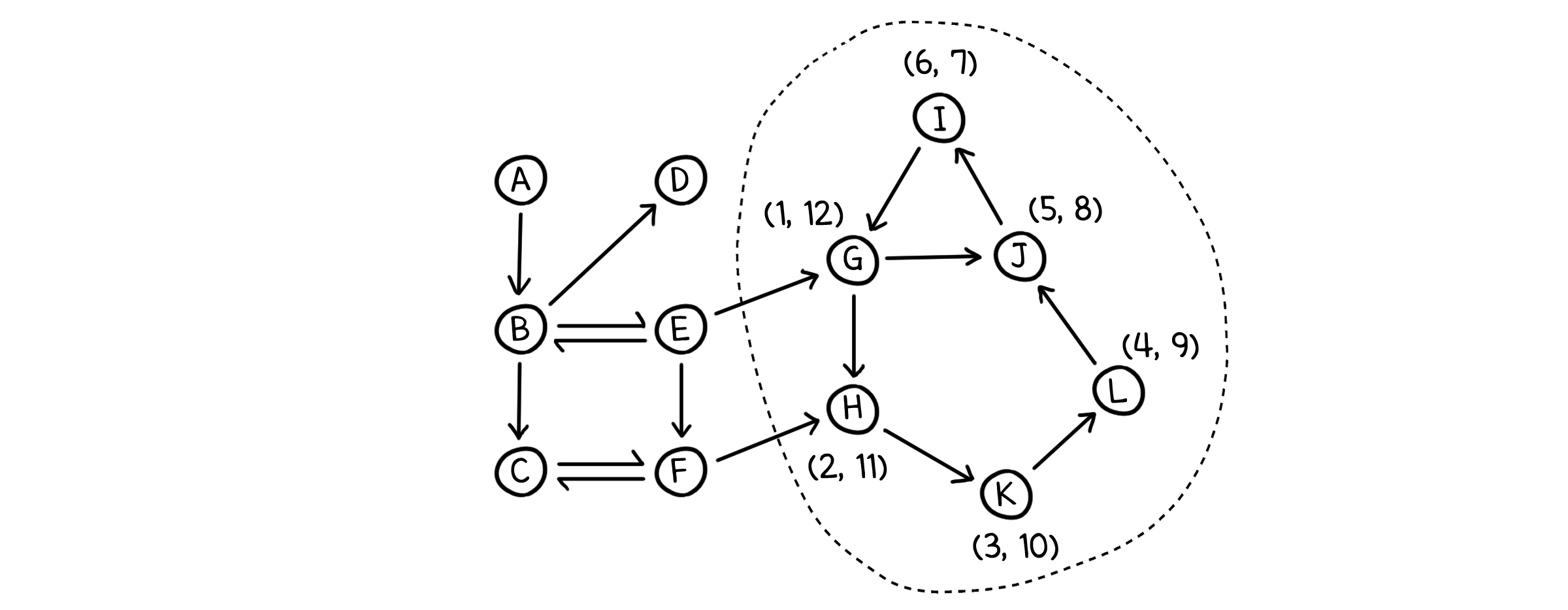
그리고 역그래프를 만든 뒤, 종료시각이 가장 늦은 노드 G 부터 다시 DFS를 진행합니다. 최상위 노드였던 G는 반대로 최하위 노드가 됩니다. 최하위 노드에서 도달할 수 있는 노드들은 같은 SCC에 속한 노드들 뿐이므로, G에서 시작한 DFS에서 방문하는 모든 노드들은 G가 포함된 SCC의 노드가 될 것입니다.
G에서 DFS가 끝나면, 그 다음으로 종료시각이 늦었던 노드 D에 대해서 DFS를 실행합니다. 이 때 최하위였던 SCC 노드들은 이미 방문한 상태이므로, 자연스럽게 탐색에서 제외됩니다. 이런 식으로 반복하면, DFS가 실행되는 단위로 SCC 노드들을 구할 수 있게 됩니다.
역 그래프를 만들어도 원래 그래프의 SCC는 동일하게 유지된다고 했었죠? 따라서, 원래 그래프의 SCC를 구할 수 있게 되었습니다!
![[CM301] 06. 그래프 (Graph)](/CMajor/assets/img/thumbnails/cm301/6.png)