[CM301] 05. 탐색 & 선택 (Searching & Selection)

 이번에는 정렬과 함께 자주 사용되는 작업인 요소를 찾는 문제에 대해 다뤄봅시다. 이는 요소를 찾는 방법에 따라 크기 탐색 문제와 선택 문제로 나눌 수 있습니다.

작성된 모든 코드는 Python의 형식을 빌린 유사 코드이며, 문법을 다소 무시한 부분이 있기 때문에 실행이 되지 않습니다.

탐색 (Searching)

 탐색(Searching) 문제는 주어진 배열에서 특정 값 $a$를 가지는 요소를 찾아 그 위치를 반환하는 것이 목표입니다. 몇 가지 대표적인 탐색 알고리즘과 그 복잡도에 대해 다뤄보겠습니다.

선형탐색 (Linear search)

def linear_search(x[1, ..., n], a):
  i = 1
  while i <= n and x != a:  # 순회가 끝나거나 a를 찾을 때 까지
    i += 1  # 순회
  
  if i <= n:  # 만약 순회가 끝나기 전에 찾았으면
    result = i  # 그 때의 인덱스 반환
  else:  # 순회가 끝나 멈췄으면
    result = 0  # 찾지 못했으므로 0 반환

  return result

 선형탐색은 처음부터 끝까지 순회하며 일치하는 값을 찾는 제일 단순한 방법입니다. 모든 요소를 하나씩 비교하기 때문에 탐색이 가능합니다.

 최악의 경우는 찾는 요소가 배열 맨 끝에 있을 때입니다. 이 경우 순회를 끝까지 진행하므로, 시간 복잡도는 $O(n)$입니다. 추가 메모리를 쓰지 않기에 공간 복잡도는 $O(1)$입니다.

이진탐색 (Binary search)

def binary_search(x[1, ..., n], a):
  i = 1  # 처음
  j = n  # 끝

  while i < j:  # i와 j나 만날 때 까지
    m = floor((i + j) / 2)  # i와 j의 중간 (내림연산)
    
    if a > x[m]:  # a가 중간값보다 크면
      i = m + 1  # 중간 ~ 끝 구간에서 반복
    else:  # a가 중간값보다 작거나 같으면
      j = m  # 처음 ~ 중간 구간에서 반복
  
  if a = x[i]:  # a를 찾았으면
    result = i  # 그 때의 인덱스 반환
  else:  # 순회가 끝나 멈췄으면
    result = 0  # 찾지 못했으므로 0 반환
  
  return result

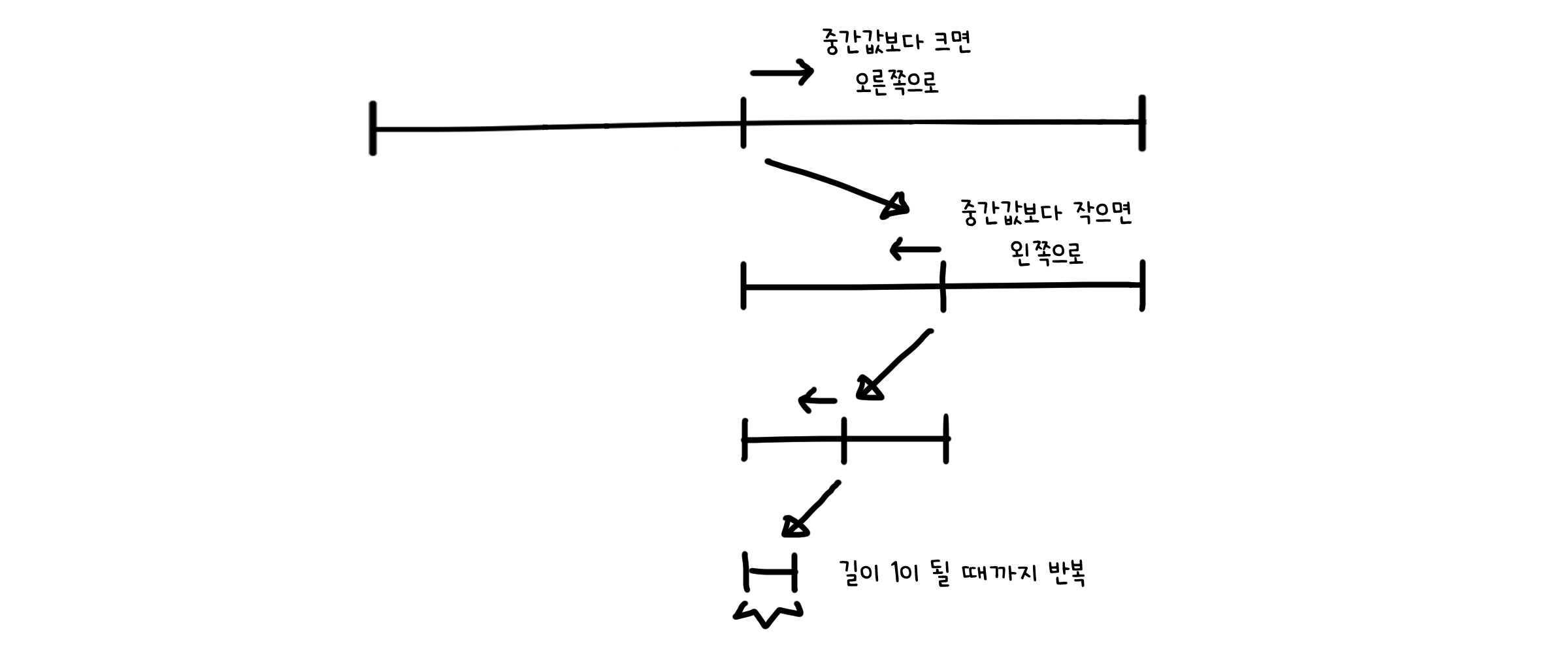
 이진탐색은 찾는 값은 배열의 중간값과 비교하며 탐색 구간을 줄이는 방법입니다. 이를 위해서 배열은 반드시 오름차순으로 정렬되어 있어야 합니다. 정렬되었을 경우 a보다 크거나 작은 구간을 배제하여 요소가 존재하는 구간만을 선택하기 때문에 탐색이 가능합니다.

 배열의 상태나 요소의 위치와 관계 없이 i와 j가 만날 때까지 반복되기 때문에 특별히 최악의 경우나 최선의 경우가 없습니다. 시간 복잡도는 $O(\log{n})$이 되고, 추가 메모리를 쓰지 않기에 공간 복잡도는 $O(1)$입니다.

선택 (Selection)

 선택(Selection) 문제는 주어진 배열에서 $k$번째로 작은 요소를 찾아 그 값을 반환하는 것이 목표입니다(물론 $k$번째로 큰 요소가 될 수도 있도 또 다른 조건이 될 수도 있지만, 여기서는 작은 값을 조건으로 하겠습니다). 탐색과는 달리 값 자체가 아니라, 특정 조건을 만족하는 요소를 찾는다는 차이가 있습니다. 몇 가지 대표적인 선택 알고리즘과 그 복잡도에 대해 다뤄보겠습니다.

정렬선택 (Sorting)

def sorting_selection(x[1, ..., n], k):
  x.sort()  # 정렬(어떤 방식으로든)
  return x[k-1]  # k-1번째 요소 반환

 가장 단순한 방법은 배열을 모두 정렬한 뒤, 인덱스 k(0부터 시작하면 k-1)의 값을 반환하는 것입니다. 우리는 앞서 정렬에 대해 다루면서 그 하한선이 $O(n\log{n})$임을 알았습니다(하한선은 최악의 경우에 대한 최솟값임을 기억하세요). 즉, 이 경우 시간 복잡도는 $O(n\log{n})$이 되는 것이죠.

  하지만 우리는 k번째로 작은 값만 알고 싶은 것이지, 모든 수의 대소관계 까지는 몰라도 상관 없습니다. 그렇다면 좀 더 좋은 방법을 찾을 수 있지 않을까요?

랜덤 분할 정복 (Randomized Divide & Conquer)

def rand_divide_conquer(x[1, ..., n], p, q, k):
  if p == q:
    return x[p]
  
  r = rand_partition(x[1, ..., n], p, q)  # 기준점의 위치 r
  i = r - p + 1  # 시작점으로부터 기준점까지의 길이 i


  if k < i:  # k번째가 i보다 앞이라면
    return rand_divide_conquer(x[1, ..., n], p, r-1, k)  # 앞 구간에서 k번째 찾기
  else if k > i:  # k번째가 i보다 뒤라면
    return rand_divide_conquer(x[1, ..., n], r+1, q, k-i)  # 뒤 구간에서 k-i번째 찾기
  else:  # 만약 i가 정확히 k번째라면
    return x[r]  # 그대로 반환

# 기준점을 무작위로 골라 그 보다 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 분리
def rand_parition(x[1, ..., n], p, q):
  rand_idx = random(p, q)  # p ~ q번째 중 무작위 요소를 선택해
  pivot = x[rand_idx]  # 기준점으로 설정
  change x[rand_idx], rand[p]  # 기준점은 앞으로 보내기
  i = p  # 왼쪽 부분의 끝 위치
  for j := p+1 to q:
    if x[j] <= pivot:  # pivot보다 작은 값은
      i += 1  # 왼쪽 부분의 끝으로
      change x[i], x[j]  # 이동
    # pivot보다 큰 값은 오른쪽으로 밀려남
  change x[p], x[i]  # 분리가 끝나면 pivot을 두 구간 사이로 이동

  return i

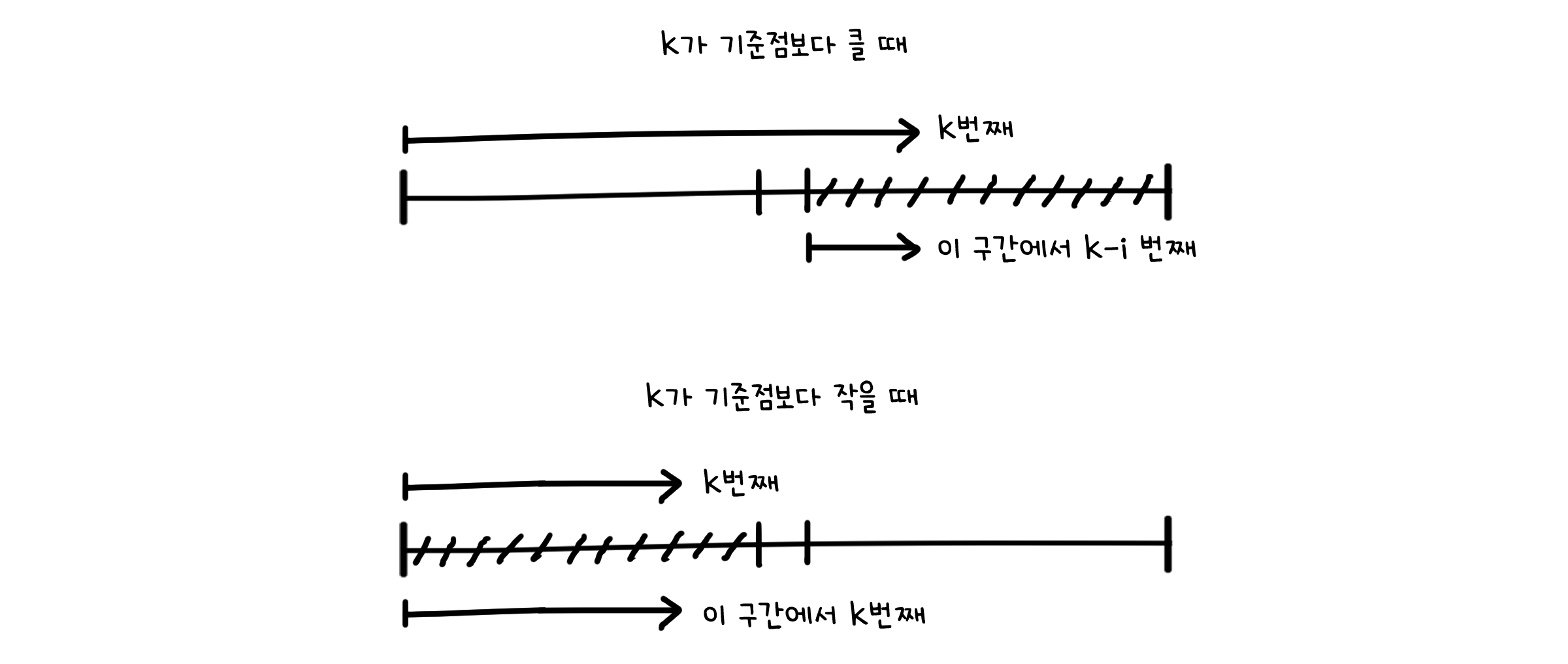
 랜덤 분할 정복은 이진탐색과 같이 배열을 둘로 나누어 값을 찾는 방법입니다. 다른 점은, 반으로 나눌 기준점을 무작위로 정한다는 것입니다. 코드에서 익숙한 부분이 보이지 않나요? 이전 장에서 다루었던 랜덤 퀵정렬의 parition() 함수를 그대로 사용하였습니다. 이렇게 하면 기준점에서 왼쪽에 있는 값들은 모두 기준점 값보다 작고, 오른쪽의 값들을 기준점 값보다 크게 되도록 분리됩니다.

 만약 k가 기준점의 위치 i보다 작다면 어차피 오른쪽 값들은 k번째 값 보다 더 큰 값일 테니 대소를 비교할 필요가 없고, 반대로 k가 i보다 크다면 왼쪽의 값들은 k번째 값 보다 당연히 작을 테니 비교할 필요가 없어지죠. 굳이 모든 값의 대소를 정렬할 필요 없이 필요한 구간만 추려 재귀를 반복하면 됩니다.

 최악의 경우는 기준점이 항상 최솟값이나 최댓값을 고르는 경우입니다. 랜덤 퀵정렬 때와 마찬가지로 지독하게 운이 나빠야겠죠. 이 때의 실행 시간은 $T(n) = T(n-1) + \Theta(n)$, 즉 시간 복잡도는 $O(n^2)$입니다.

 하지만 대부분의 경우는 하위 배열이 비슷하게 분할될 것입니다. 그리고 k번째가 속하는 구간 만을 선택해 재귀를 호출할 것입니다. 두 구간중 크기가 더 큰 것을 선택한다고 가정하면, 실행시간은 다음과 같습니다.

\[T(n) = T(max \{an, bn\}) + \Theta(n) \quad (an + bn = n-1)\]

 그렇다면 우리는 랜덤 퀵정렬 때와 같은 방법으로 평균 실행 시간을 계산해볼 수 있습니다.

\[E[T(n)] = \sum_{k=0}^{n-1} \frac{1}{n} \; \left\{ E[T(max \{k, n-k-1\})] + \Theta(n) \right\}\] \[= \frac{1}{n} \; \sum_{k=0}^{n-1} E[T(max \{k, n-k-1\})] + \Theta(n)\]

  $max(a, b)$는 a와 b가 바뀌어도 똑같으니까

\[E[T(n)] \leq \frac{2}{n} \; \sum_{k=floor(n/2)}^{n-1} E[T(k)] + \Theta(n)\]

 똑같이 이 식의 상한선이 무엇인지를 알기 위해 대입(substitution)법을 사용해봐야겠죠. $k < n$인 경우에 대해 $E[T(k)] \leq ck$라고 가정하겠습니다.

\[E[T(n)] \leq \frac{2}{n} \; \sum_{k=floor(n/2)}^{n-1} ck + \Theta(n)\]

 이미 알려식 계산식으로 약간의 트릭을 사용하겠습니다.

\[\sum_{k=floor(n/2)}^{n-1}k \leq \frac{3}{8}n^2\]

 이 사실을 사용할거에요(그래서 k를 미리 반으로 접어 놓은 거에요).

\[E[T(n)] \leq \frac{2c}{n} * \frac{3}{8} n^2 + \Theta(n) = \frac{3}{4}cn + \Theta(n) = cn - (\frac{c}{4}n - \Theta(n))\]

 $E[T(n)] \leq cn$을 만족하기 위해서는 $\frac{c}{4}n - \Theta(n) \geq 0$이 성립하기만 하면 됩니다. 따라서 이 조건을 만족할 수 있을 만큼 충분히 큰 $c$를 잡는다면, $E[T(n)] \leq cn$임을 보일 수 있고, 따라서

\[E[T(n)] = O(n) \quad \Box\]

 즉, 평균적으로는 $O(n)$시간만 걸리게 됩니다.

중간-중간값 알고리즘 (Medians of medians algorithm)

 랜덤 분할 정복은 평균적으로 O(n)이지만 기준점이 나쁘게 잡히면 굉장히 좋지 않은데($O(n^2)$), 최악의 경우에도 O(n) 을 보장하는 알고리즘이 있습니다. 이는 중간-중-중간(median-of-medians), 혹은 제안자 다섯의 이름을 따 Blum-Floyd-Pratt-Rivest-Tarjan (BFPRT) 알고리즘이라고도 부릅니다.

 각설하고 코드를 보여드리겠습니다.

def BFPRT(x[1, ..., n], k):
  if n <= 25:  # 크기가 25 이하라면
    use brute_force()  # 직접 찾기
  else:
    m = ceil(n/5)  # n을 5등분 (올림 계산)
    
    for i := 1 to m:  # 5등분한 배열마다
      y[i] = BFPRT(y[5i - 4, ..., 5i], 3)  # 중간값(3번째) 찾기
    
    mom = BFPRT(y[1, ..., m], floor(m/2))  # 중간값 중에서도 중간값 찾기

    r = partition(x[1, ..., n], mom) # 중간-중간값을 기준으로 구간 분할

    if k < r:  # 만약 k번째가 r보다 앞이라면
      return BFPRT(x[1, ..., r-1], k)  # 앞 구간에서 k번째 찾기
    else if k > r:  # aksdir k번째가 r보다 뒤라면
      return BFPRT(x[r+1, ..., n], k-r)  # 뒤 구간에서 k-r번째 찾기
    else:  # 만약 r이 정확히 k번째라면
      return mom  # 그대로 반환

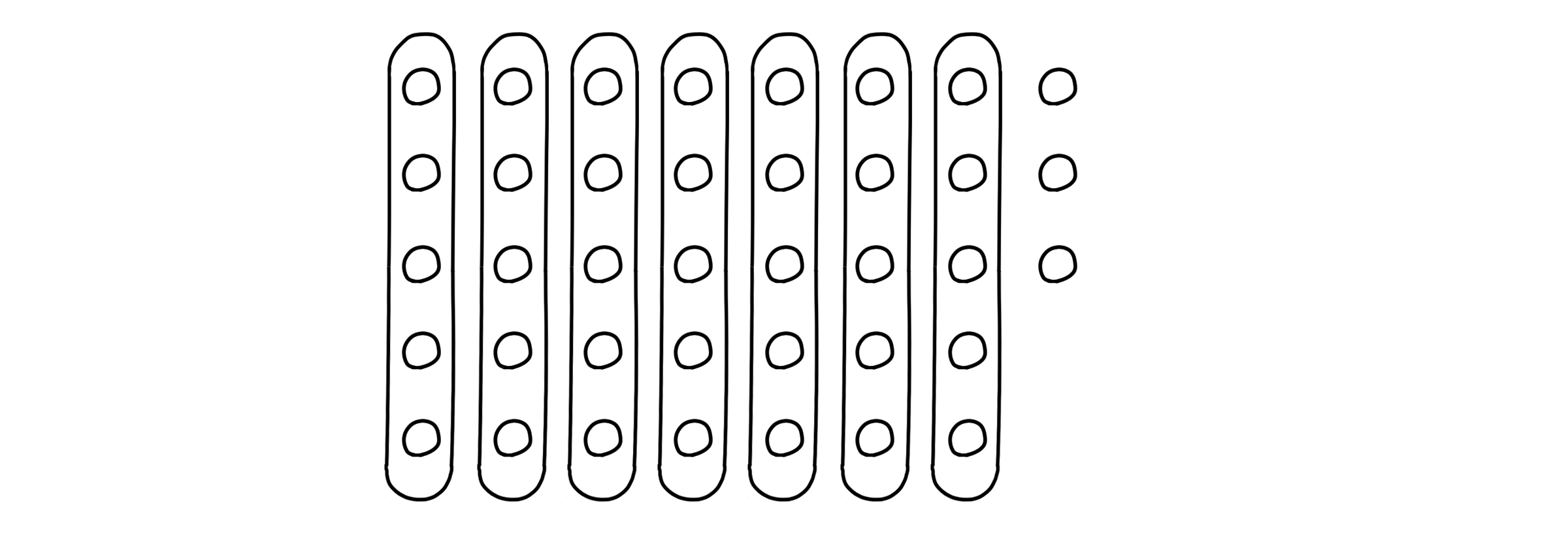
 도망가지 말아요, 천천히 풀어봅시다. 우선 적당한 길이의 배열을 준비했습니다.

 이것을 길이 5의 작은 배열들 m개로 나눠봅시다. 대소관계 필요없이 완전히 무작위로 묶습니다.

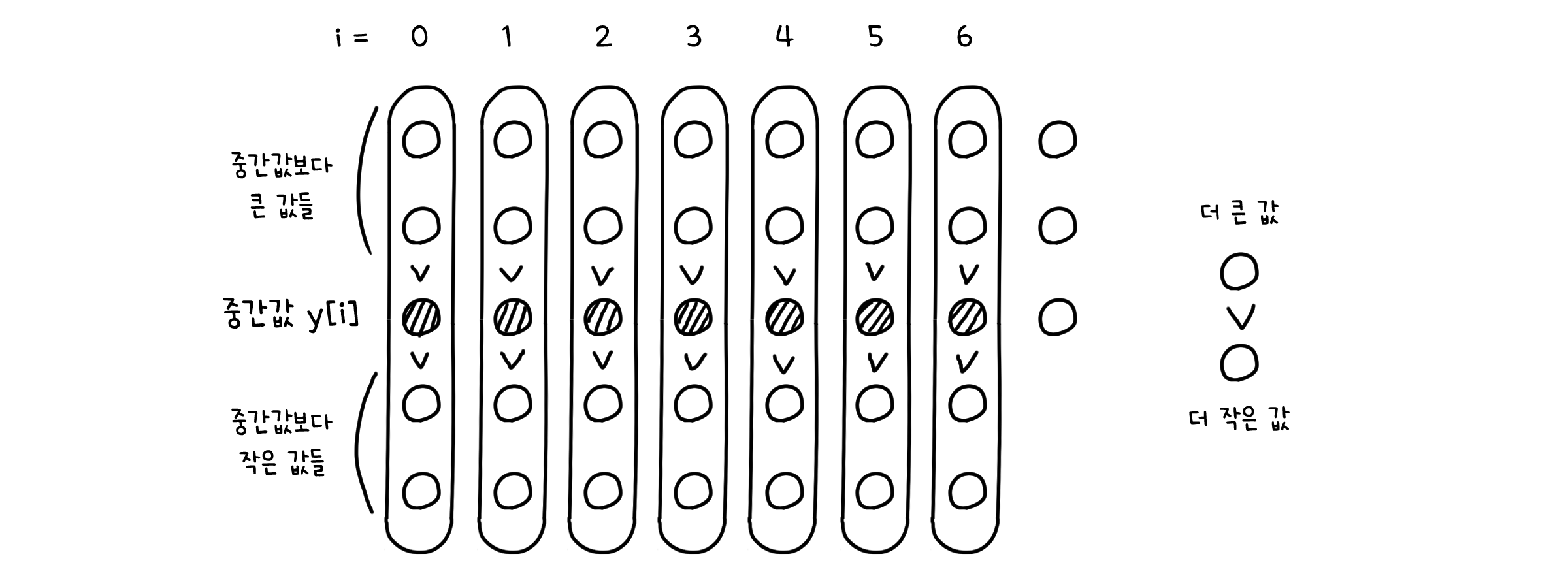
 그리고 작은 배열들마다 3번째로 작은 값, 그러니까 중간값을 찾습니다. m개의 중간값들이 나올 것입니다(실제로 partition 함수처럼 중간값을 기준으로 구간을 나누지는 않지만, 이해를 돕기 위해 두 구간을 나누었습니다). 이들의 배열을 새로이 y[1, …, m]라고 정의했네요.

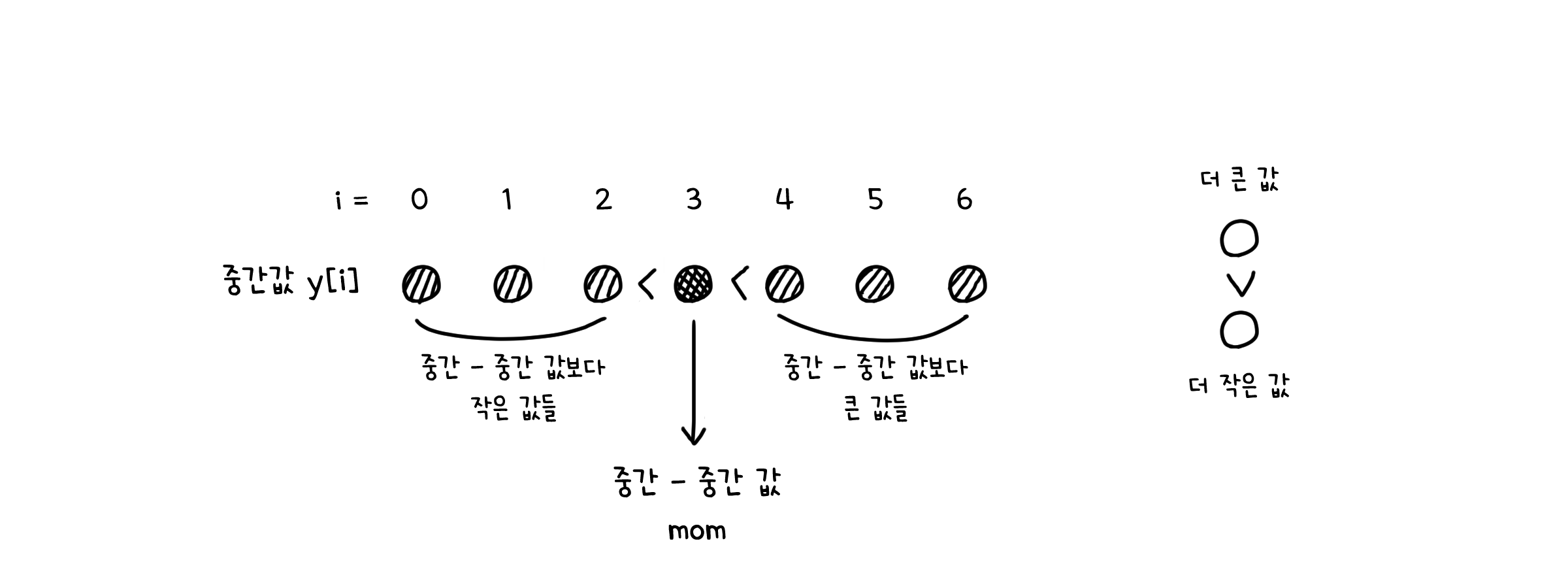
 이제 y에서도 중간값을 찾습니다. 즉 중간값들 중에서도 중간-중간값을 찾는 것이죠(역시 실제로는 partition 함수처럼 구간을 나누지는 않습니다!).

 그 후부터는 중간-중간값을 기준점으로 해서 분할 정복과 똑같은 동작을 하는 것을 볼 수 있습니다. 두 구간으로 가르고, 재귀 호출… 이런 것들이요. 그렇다면 이게 어떻게 $O(n)$의 시간 밖에 걸리지 않는 것일까요?

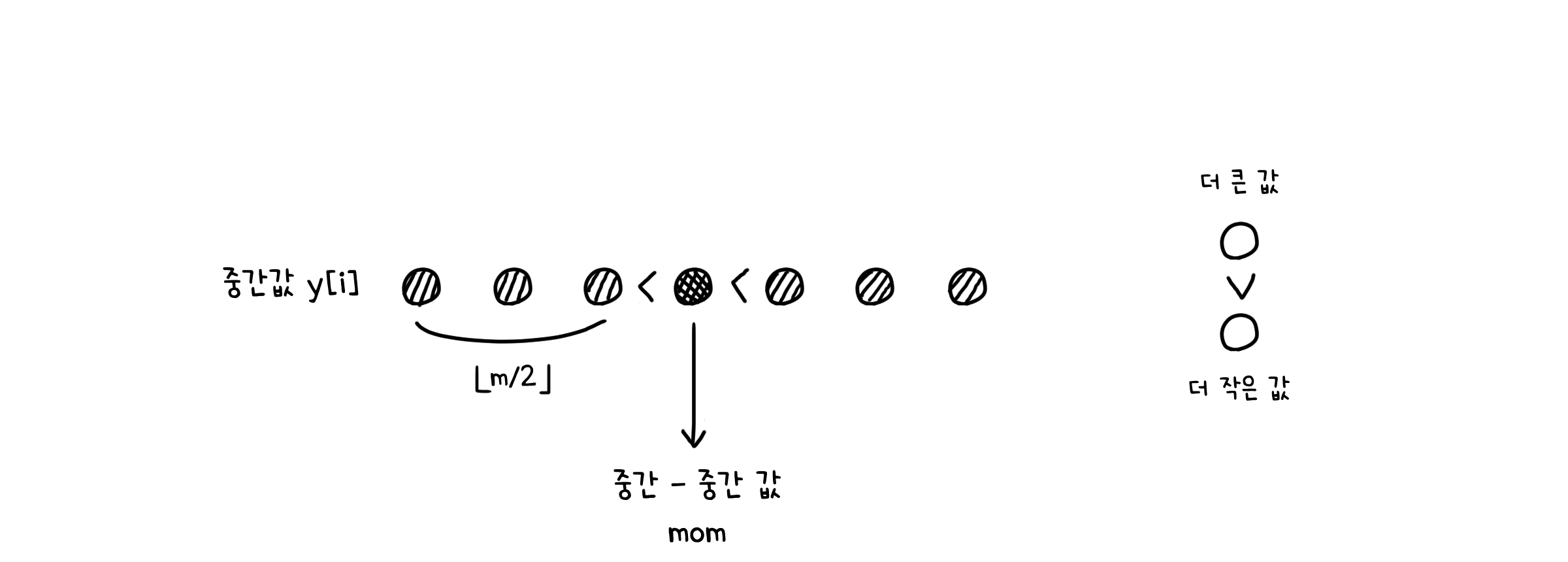
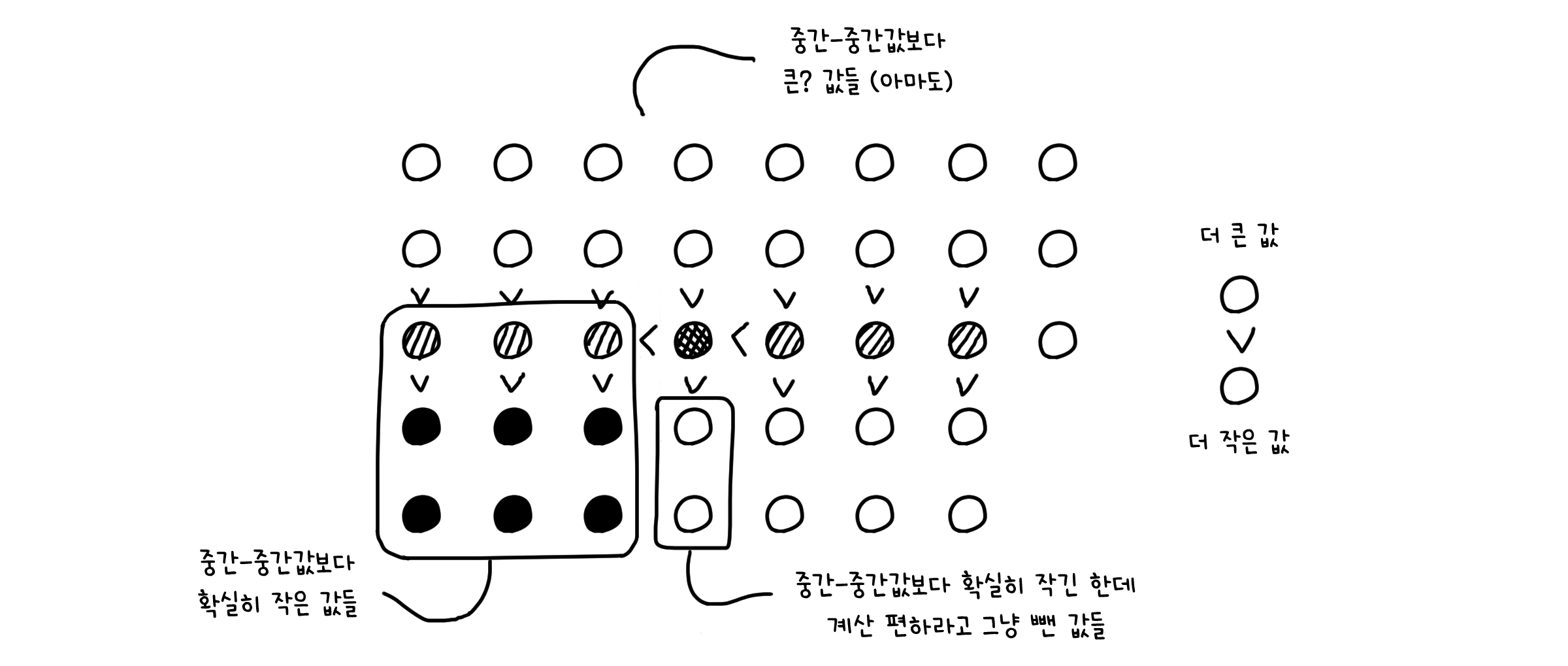
 일단 중간-중간값은 최소한 배열 y의 절반, 그러니까 $\lfloor \frac{m}{2} \rfloor$ 만큼의 값들보다는 큰 값입니다.

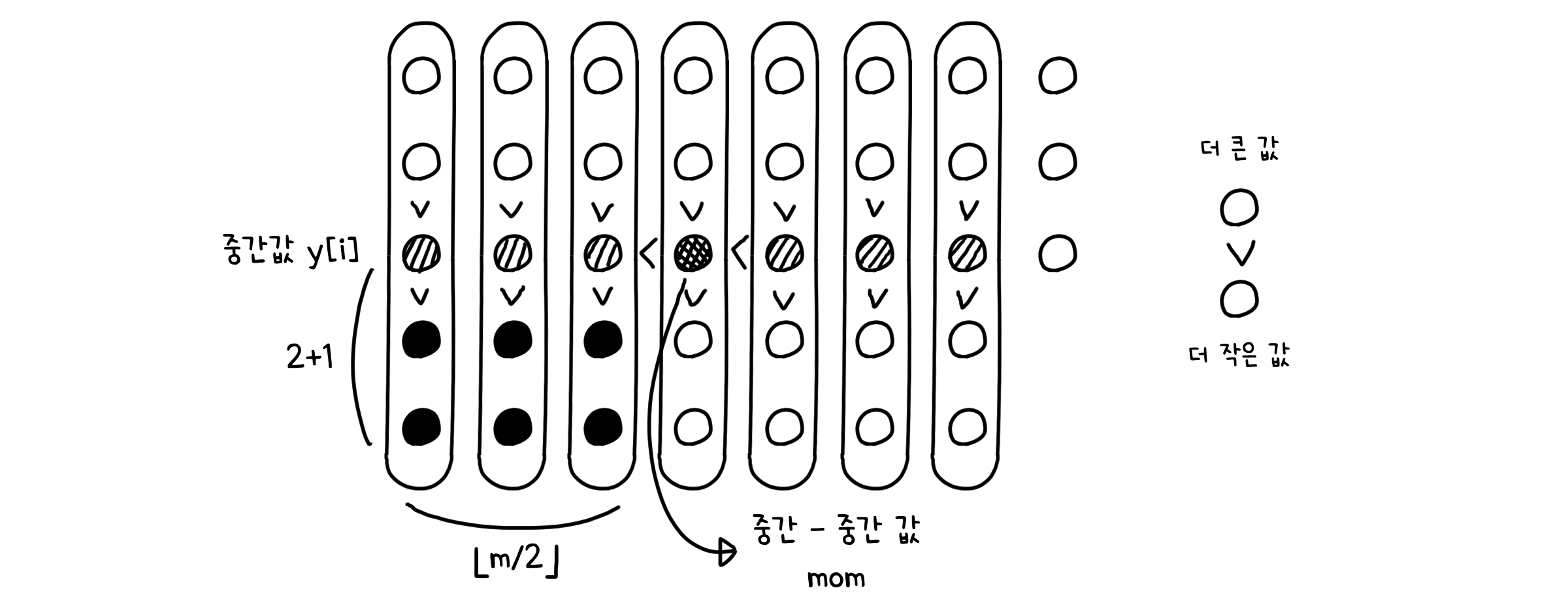
 그리고 배열 y에 속한 값들은 길이가 5인 배열의 중간값입니다. 때문에 이들보다 작은 두 개의 값이 반드시 존재할 것입니다.

 그러므로 중간-중간값은 적어도 $\lfloor \frac{m}{2} \rfloor * 3$ 개의 값보다는 큰 값이 되는 것이죠. 그런데 m은 길이 n을 5로 나누었을 때의 몫이죠? 그렇기 때문에 $m = \lfloor \frac{n}{5} \rfloor$ 로 나타낼 수 있습니다.

 따라서 중간-중간값은 항상 그 보다 작은 $\lfloor \lfloor \frac{n}{5} \rfloor \frac{1}{2} \rfloor * 3 \sim \frac{3}{10}n$ 개의 값을 가지게 됩니다. 다르게 말하면, 중간-중간값은 그보다 큰 최대 $\frac{7}{10}n$ 개의 값을 가질 수 있다는 뜻입니다. 그러니 최악의 경우, 이 알고리즘은 $\frac{7}{10}n$ 길이의 하위 배열로 재귀를 호출하게 됩니다.

 이제 총 계산량을 종합해봅시다.

• 중앙값 m개를 찾는데 걸리는 시간 : 각 길이 5짜리 배열에서 중앙값들을 찾을 때는 5개 요소를 모두 순회합니다. 따라서 모든 중앙값들을 찾으면 배열 전체를 순회하는 것과 같기 때문에 $O(n)$입니다.

• 중간-중간값을 찾는데 필요한 시간 : 배열 y의 길이 만큼, 즉 $O(n/5)$입니다.

• 재귀로 호출되는 하위배열의 크기 : 최악의 경우 $\frac{7}{10}n$입니다.

 따라서 중간-중간값 알고리즘의 회귀식은

\[T(n) \leq T(n/5) + T(7n/10) + O(n)\]

 대입(Substitution)법을 사용하겠습니다. $T(k) < ck \; (k < n)$ 라고 가정할 때

\[T(n) \leq cn/5 + 7cn/10 + O(n) = 9cn/10 + O(n) = O(n)\]

 그러므로 중간-중간값 알고리즘의 시간 복잡도는 $O(n)$, 즉 항상 선형 시간 안에 끝낼 수 있게 됩니다.