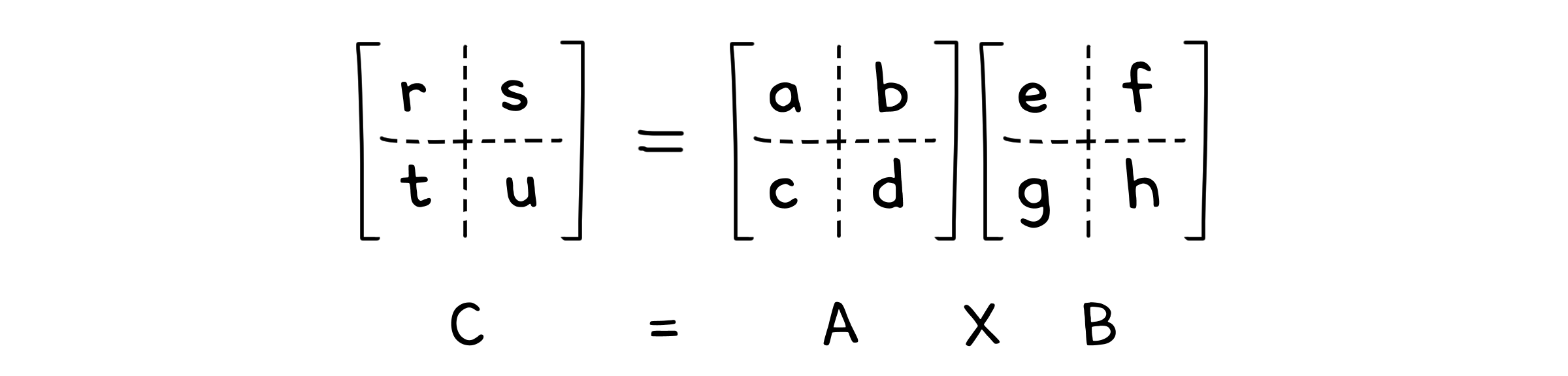[CM301] 03. 회귀(Recurrence)

분할과 정복 (Divide and Conquer)

 살다보면 미친듯이 바빠지는 때가 있습니다. 해야 하는 일이 너무 복잡해져, 감히 어디부터 손 대야 할 지 짐작조차 가지 않을 정도로요. 그저 앉아서 점심 메뉴나 고민할 뿐이죠.

 하지만 우리 모두 해결방법은 알고 있습니다. 해야 할 일 항목을 만들어서, 당장 할 수 있는 작은 일 부터 차근차근 처리하는 것입니다. 그렇게 하면 아무리 거대하고 복잡해 보이는 문제라 하더라도, 어느새 해결해버린 자신을 볼 수 있을겁니다. 이번에 소개할 알고리즘 또한 같은 방식을 사용합니다. 문제를 분할하고 하나씩 정복하는 것이죠.

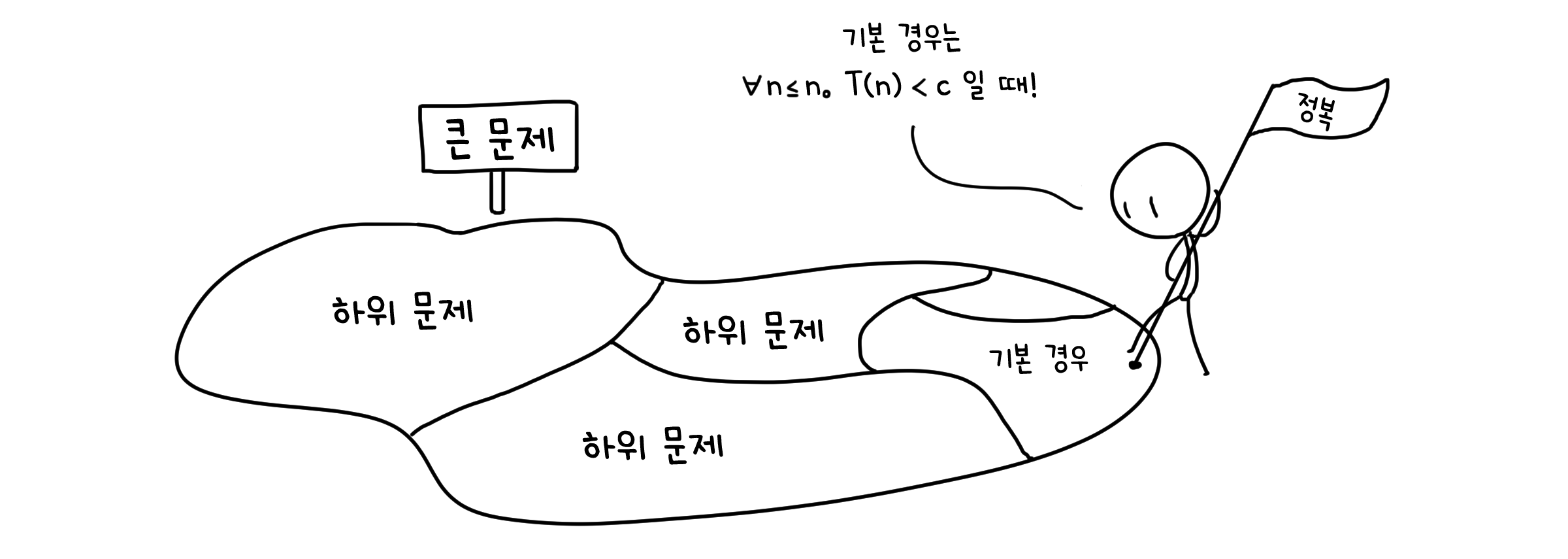
 분할(Divide) 단계는 문제를 좀 더 작은 하위문제(Subproblem)들로 나누는 과정입니다. 하위 문제들은 더 이상 시간이 짧아질 수 없는 기본적인 문제가 될 때 까지 계속해서 분할될 것입니다. 정복(Conquer) 단계는 분할했던 하위문제들을 해결하는 과정입니다 기본 경우에서부터 시작합니다. 병합(Combine) 단계는 해결한 하위문제들을 서로 합쳐 더 큰 하위문제로 만드는 과정입니다. 분할했던 문제들을 다시 하나씩 합쳐서 가장 큰 원래 문제의 해답을 찾는 것입니다.

병합정렬 (Merge sort)

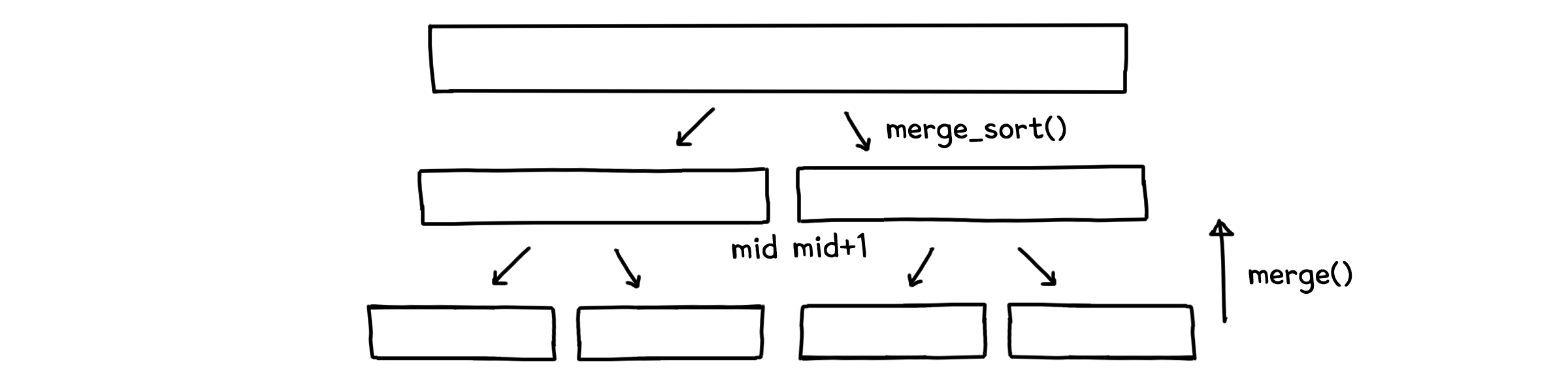
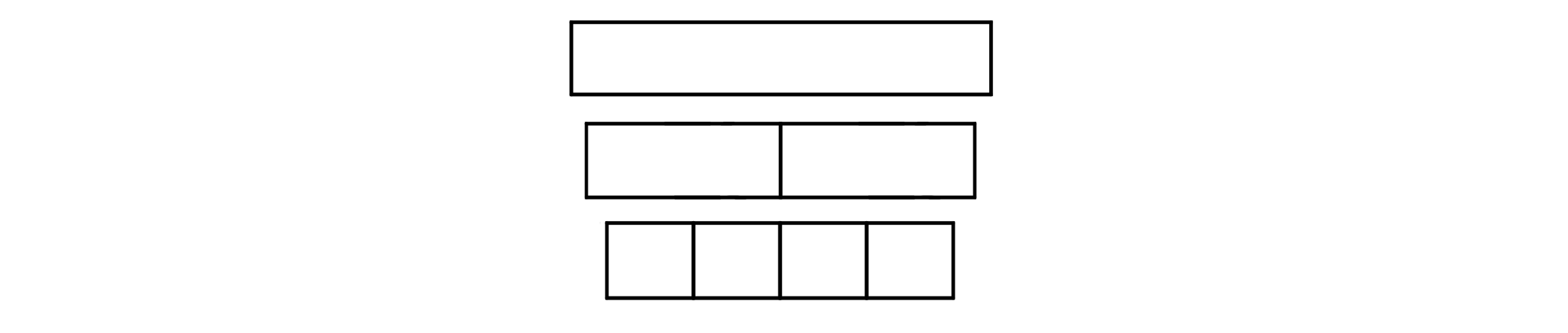
 분할 정복을 이용한 대표적인 알고리즘이 병합정렬(Merge sort)입니다. 처음 배열을 길이가 짧은 하위 배열들로 쪼개서 정렬한 다음 정렬된 배열들을 다시 합치는 방법을 사용합니다.

## Merge sort ##
def merge_sort(a[1, ..., n]):
  if n > 1:
    mid = floor(n/2)  # mid는 배열 길이의 절반 위치(내림 계산)
    return merge(merge_sort(a[1, ..., n/2]), merge_sort(a[n/2 + 1, ..., n]))  # 기본 경우가 아니면 배열을 반으로 분할
  else:
    return a  # 기본 경우는 배열 길이가 1일 때. 배열을 그대로 반환


def merge(x[1, ..., p], y[1, ..., q]):
  if p=0: return y[1, ..., q]  # x가 비었으면, y만 반환
  if q=0: return x[1, ..., p]  # y가 비었으면, x만 반환

  if x[1] <= y[1]:  # 각 배열의 첫째를 비교해서
    return x[1] + merge(x[2, ..., p], y[1, ..., q])  # x[1]이 더 작으면 맨 앞에 두고 나머지 마저 병합
  else:
    return y[1] + merge(x[1, ..., p], y[2, ..., q])  # y[1]이 더 작으면 맨 앞에 두고 나머지 마저 병합

 병합정렬의 실행시간에 대해 알아봅시다. 우리는 두 가지 부분에서 계산 시간이 발생함을 알 수 있습니다. 1. 하위 문제를 처리할 때 걸리는 시간과 2. 분할 및 병합에 걸리는 시간이죠. 하위문제는 본 문제에서 다루는 배열의 절반만 사용하니 시간도 절반($T(n/2)$)이 될 것입니다.
 분할 및 병합은 코드를 잘 봐야 하는데, 병합(merge 함수) 단계를 보면 어느 한 쪽의 배열이 빌 때 까지 각 배열의 첫 번째 요소를 비교하는 것을 알 수 있습니다. x, y 모두 본 문제의 배열에서부터 분할된 배열이기 때문에, 총 길이는 n이 됩니다. 그러니 병합을 위해 걸리는 시간도 n에 비례하게 되겠죠. 따라서 걸리는 시간은 $\Theta(n)$이 될 것입니다. 정리하자면, 병합정렬에서 걸리는 시간은 아래와 같이 나타낼 수 있습니다.

회귀 (Recurrence)

 앞선 병합정렬의 시간식을 점화식의 형태로 표현했습니다. 이렇게 어떤 수열을 이전 항들의 관계식으로 정의한 것을 회귀(Recurrence)라고 합니다. 회귀는 병합정렬 뿐 아니라 다른 재귀함수를 사용한 알고리즘을 표현할 때도 필수적으로 사용됩니다.

회귀(Recurrence)는 재귀(Recursion)와 영어 단어가 비슷해 헷갈릴 수 있지만, 조금 다른 개념입니다. 재귀는 어떤 함수가 자기 자신을 직접 또는 간접적으로 다시 호출하는 것, 즉 프로그램의 실행 과정에서 일어나는 현상입니다.

 물론 점화식이 그렇듯, 회귀를 통해 표현한 시간식을 온전한 형태로 다시 쓸 수도 있습니다. 회귀식을 풀 때는 몇 가지 대표적인 방법들을 사용합니다.

전개 (Unrolling)

 직접 점화식의 이전 항에 대입하여 푸는 방법입니다. $T(n)$를 $T(n/2)$에 대한 식으로, 다시 $T(n/4)$에 대한 식으로… 반복해서 펼쳐주는 것이죠.

 아직 다루지는 않았지만, 선택정렬(Selection sort)로 예를 들어보겠습니다. 선택정렬을 회귀식으로 나타내면 다음과 같습니다.

\[T(n) = T(n-1) + cn\]

 이제 $T(n-1)$ 항을 기본 경우가 나올 때 까지 계속 풀어줄겁니다.

\[T(n) = T(n-2) + c(n-1) + cn = T(n-3) + c(n-2) + c(n-1) + cn = ...\]

 전부 다 풀면 이런 수식이 될겁니다.

\[T(n) = c + 2c + ... + c(n-1) + cn\]

 이걸 간단하게 정리해보죠.

\[T(n) = c \times \frac{n(n-1)}{2} \leq cn^2\]

 그리하여, 우리는 정확한 실행시간을 구할 수 있습니다.

\[T(n) = \Theta(n^2)\]

 복잡한 식에는 비효율적이지만, 직관적이고 간단한 방법입니다.

대입 (Substitution)

 수학적 귀납법을 이용한 방법입니다. 먼저 $T(n)=O(g(n))$이라고 가정하고, 귀납법에 모순이 없음을 보이는 방법이죠. 아래 경우를 예로 들어봅시다.

\[T(n) = 4T(n/2) + n\]

첫 번째 시도

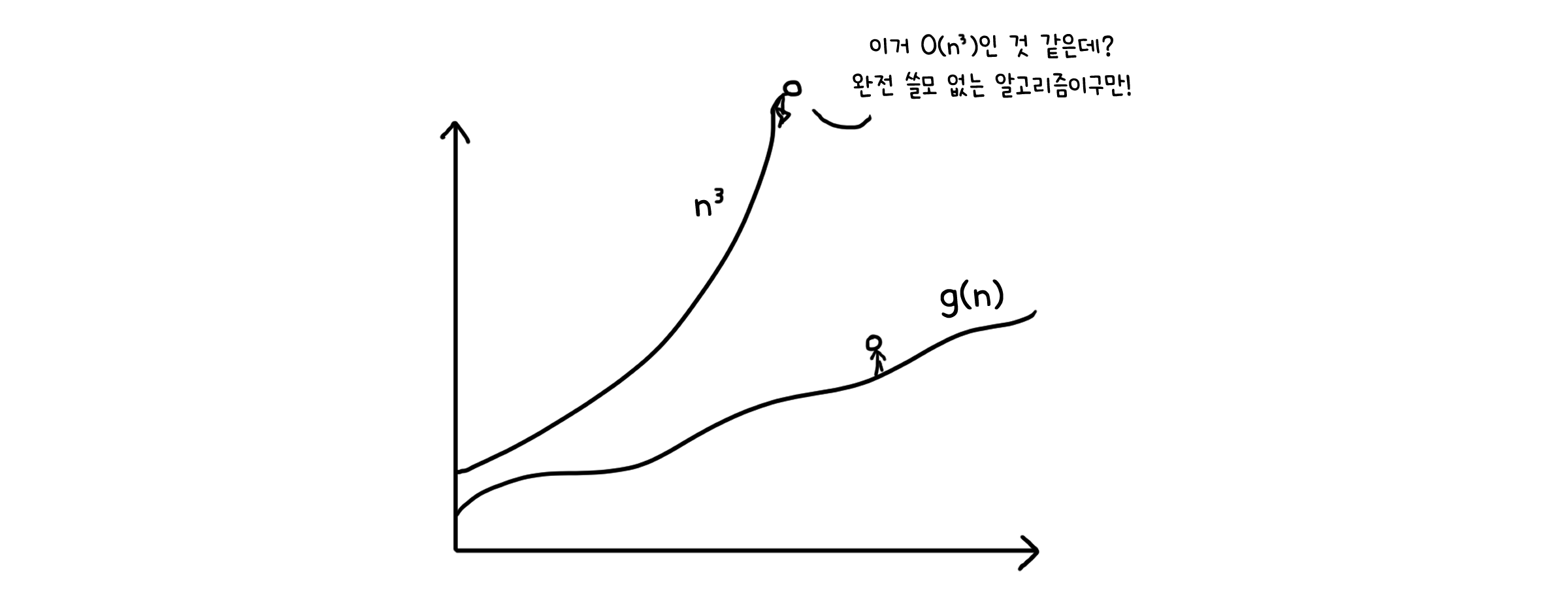
 일단 상한선이 $T(n) = O(n^3)$일 것이라고 가정하고 이를 증명할 것입니다. $T(k) \leq ck^3 \; (k < n)$이라고 할 때, 이를 토대로 아래와 같이 정리할 수 있습니다.

\[T(n) \; \leq \; 4c(\frac{n}{2})^3 + n \; = \; \frac{c}{2}n^3 + n \; \leq \; cn^3\]

 별 다른 조건 없이 $T(n) = O(n^3)$임을 보일 수 있긴 합니다. 그런데 이게 뭐가 문제냐고요? 상한성인데에 문제는 없습니다. 다만, 그 상한선이 불필요하게 높게 잡혔다는 것이 문제이죠. 특별한 조건이 없다는 것은, 너무 당연하게 크다는 뜻입니다. 우리가 원하는 상한선은 어느 시점 부터 $T(n) \; \leq \; cn^3$가 되기만 하면 되기 때문에 우리는 상한선을 좀 더 낮춰 잡아볼 수 있습니다.

두 번째 시도

 그렇다면 상한선이 $T(n) = O(n^2)$일 것이라고 가정해봅시다. $T(k) \leq ck^2 \; (k < n)$이라고 할 때, 이를 토대로 아래와 같이 정리할 수 있습니다.

\[T(n) \; \leq \; 4c(\frac{n}{2})^2 + n \; = \; cn^2 + n\]

 $T(n) = O(n^2)$로 쓸 수 있긴 합니다. 하지만 우리가 귀납법에서 보여야 하는 것은 $T(n) \leq cn^2$입니다. $+n$가 튀어나와 있으니, 지금 이 식으로는 완벽하게 보일 수 없어요. 다시 한 번 상한선을 좀 더 낮춰 잡아야 합니다.

세 번째 시도

 이번엔 상한선을 똑같이 $T(n) = O(n^2)$로 가정하되, $T(k) \leq c_1k^2 - c_2k \; (k < n)$라고 해봅시다. 이를 토대로 아래와 같이 정리할 수 있습니다.

\[T(n) \; \leq \; 4(c_1(\frac{n}{2})^2 - c_2\frac{n}{2}) + n \; = \; c_1n^2 - c_2n - (c_2n - n) \; \leq \; c_1n^2 - c_2n \quad (c_2n - n \geq 0 일 때)\]

 이렇게 하면 $T(n) \; \leq \; c_1n^2 - c_2n$을 만족하기 위한 조건이 $c_2 > 1$ 일 때 입니다. 따라서 귀납적으로 증명 가능하면서도 납득 가능할 만큼의 상한선 $c_1n^2 - c_2n$을 찾게 되었습니다. 물론 똑같이 $T(n) = O(n^2)$로 쓰이긴 합니다.

재귀 트리 (Recursion tree)

 재귀 트리는 재귀 호출 구조를 트리 형태의 그래프로 나타냅니다. 그리고 각 깊이마다 걸리는 시간들의 합을 구해 총 시간을 계산하게 됩니다. 전개(unrolling)방식과 유사하게 진행하지만, 계산 방법이 다릅니다. 똑같이 예시를 들어보겠습니다.

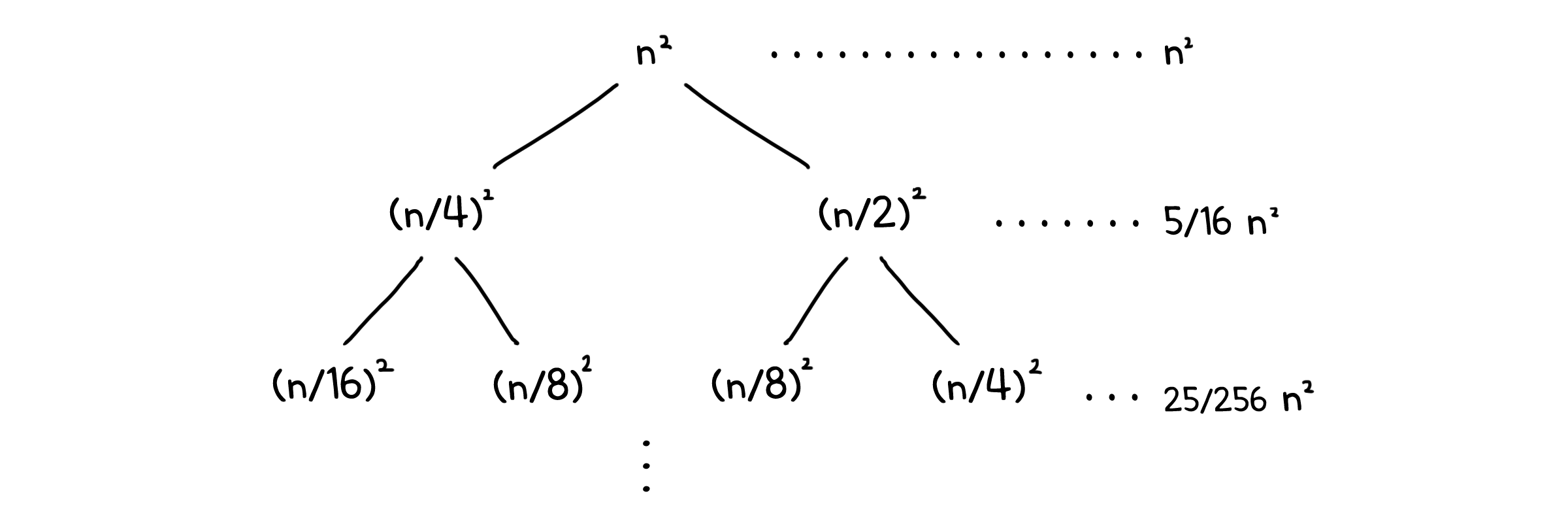
\[T(n) = T(n/4) + T(n/2) + n^2\]

 $T(n/4)$와 $T(n/2)$가 트리에서 $T(n)$ 노드의 자식이 될 것입니다. 그러면 우리는 트리의 각 깊이에 속하는 노드의 시간 총 합을 구할 수 있습니다.

 이것들을 모두 더하면 등비 수열이 나올텐데, 공비가 1보다 작은 형태이므로 등비 수열이 수렴하여, 간단히 나타낼 수 있습니다.

\[T(n) = n^2(1 + \frac{5}{16} + \frac{25}{256} + ...) = \Theta(n^2)\]

마스터 정리 (Master method)

 이번에는 앞서 사용한 재귀 트리 방법을 좀 더 응용해서, 아예 일반화된 회귀식을 해결해 봅시다.

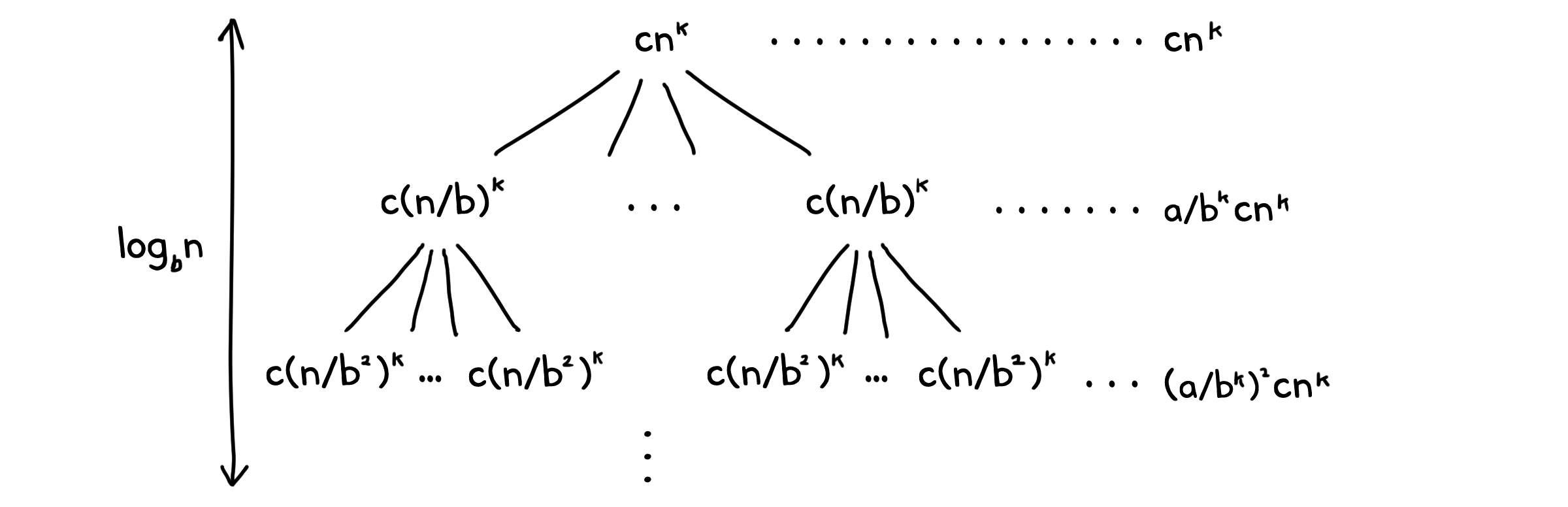
\[T(n) = aT(n/b) + cn^k\]

 우리는 이 트리에서 똑같이 깊이 별 시간의 총 합을 구할 수 있습니다.

 이제 모두 더해봅시다. 노드 당 자식의 수는 동일하므로, 트리의 깊이는 $\log_b{n}$으로 둘 수 있습니다.

\[T(n) = cn^k\{ 1 + \frac{a}{b^k} + (\frac{a}{b^k})^2 + ... + (\frac{a}{b^k})^{\log_b{n}} \}\]

 $\frac{a}{b^k} = r$로 두면, 재귀 트리 때와 같이 등비 수열을 얻을 수 있습니다.

\[T(n) = cn^k\{ 1 + r + r^2 + ... + r^{\log_b{n}} \}\]

 이제 $T(n)$의 값은 $r$의 크기에 따라 달라질 것입니다. 하나씩 살펴보도록 합시다.

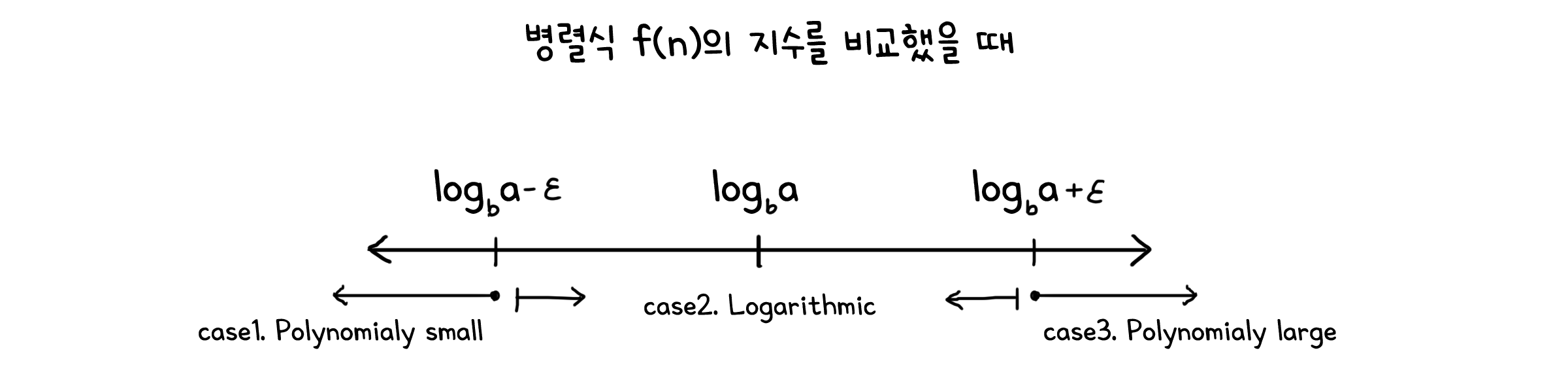
경우 1. r > 1 일 때

\[a > b^k \quad \rightarrow \quad k < \log_b{a} \quad \rightarrow \quad k \leq \log_b{(a-\epsilon)}\]

 하위 문제가 생기는 양이 하위 문제의 해결 시간보다 더 큰 경우입니다. 이 경우 문제를 해결하고 병합하는 과정은 얼마 걸리지 않지만, 하위 문제들을 호출하는 과정이 시간의 대부분을 차지하게 됩니다. $cn^k$ 항이 기준이 되는 값인 $n^{\log_b{a}}$보다 약간 작기 때문에, 다항식적으로 작은 경우(Polynomial small)라고 부릅니다.

 이 경우 $r > 1$이므로 등비수열의 항에서 $r^{\log_b{n}}$ 항이 지배적이게 됩니다.

\[T(n) = cn^k\frac{r^{\log_b{n}+1}-1}{r-1} = \Theta(cn^kr^{\log_b{n}})\]

 $r = \frac{a}{b^k}$이므로

\[T(n) = \Theta(cn^ka^{\log_b{n}}b^{-k\log_b{n}}) = \Theta(cn^ka^{\log_b{n}}n^{-k}) = \Theta(ca^{\log_b{n}})\]

 따라서 $T(n)$를 $\Theta$로 나타내면:

\[T(n) = \Theta(n^{\log_b{a}})\]

경우 2. r = 1 일 때

\[a = b^k \quad \rightarrow \quad k = \log_b{a}\]

 하위 문제가 생기는 양과 하위 문제의 해결 시간이 동일한 경우입니다. 이 경우 두 요소가 균형을 이루어 각 재귀 단계에서 발생하는 비용이 비슷하게 누적됩니다. k가 정확히 기준 로그값 $n^{\log_b{a}}$를 가지기에 로그(logarithmic) 경우라고 부를 수 있습니다.

 이 경우 r = 1을 대입하여 $T(n)$을 쉽게 계산할 수 있습니다.

\[T(n) = cn^k(\log_b{n} + 1) = \Theta(n^k \; \log{n})\]

 만약 다항식 외의 항이 더 붙어 $T(n) = n^{\log_b{a}} \; (\log{n})^k$ 일때, $\Theta$로 나타내면:

\[T(n) = \Theta(n^{\log_b{a}} \; (\log{n})^{k+1})\]

경우 3. r < 1 일 때

\[a < b^k \quad \rightarrow \quad k > \log_b{a} \quad \rightarrow \quad k \geq \log_b{(a+\epsilon)}\]

 하위 문제가 생기는 양 보다 하위 문제의 해결 시간이 더 큰 경우입니다. 이 경우 하위 문제들을 호출하는 과정보다 문제를 해결하고 병합하는 과정이 시간을 더 많이 사용합니다.$cn^k$ 항이 기준이 되는 값인 $n^{\log_b{a}}$보다 약간 크기 때문에, 다항식적으로 큰 경우(Polynomial large)라고 부릅니다.

 이 경우 $r < 1$이므로 등비수열의 항에서 $1$ 항이 지배적이게 됩니다.

\[T(n) = cn^k\frac{1-r^{\log_b{n}+1}}{1-r} = \Theta(cn^k)\]

 등비 수열 항이 전부 사라지는 것이므로, 만약 병합 항이 $cn^k$이 아니라 일반적인 식 $f(n)$이어도 그대로 쓸 수 있습니다.

\[T(n) = f(n)\frac{1-r^{\log_b{n}+1}}{1-r} = \Theta(f(n))\]

 따라서 $T(n)$를 $\Theta$로 나타내면:

\[T(n) = \Theta(f(n))\]

 마스터 정리는 회귀가 얼마나 빠르게 분화되는지를 기준으로 경우를 나누어 실행시간을 계산할 수 있습니다. 분화가 하위 문제가 작아지는 속도 보다 빠르면 걷잡을 수 없이 커지겠지만, 문제의 크기는 무한하지 않고 트리의 깊이도 유한하니까 상관은 없겠죠.

 표를 통해 정리해보면 이렇게 됩니다.

$f(n)$	$T(n)$	경우	예시
$O(n^{\log_b{a}-\epsilon})$	$\Theta(n^{\log_b{a}})$	분화가 문제 해결보다 빠름	$T(n)=4T(n/2)+n \rightarrow \Theta(n^2)$
$\Theta(n^{\log_b{a}}(\log{n})^k)$	$\Theta(n^{\log_b{a}}(\log{n})^{k+1})$	분화와 문제 해결이 비슷함	$T(n)=4T(n/2)+n^2 \rightarrow \Theta(n^3)$
$\Omega(n^{\log_b{a}+\epsilon})$	$\Theta(f(n))$	분화가 문제 해결보다 느림	$T(n)=4T(n/2)+n^3 \rightarrow \Theta(n^4)$

 병합정렬의 회귀식은 $2T(n/2) + \Theta(n)$이었습니다. 마스터 정리를 따른다면, 병합정렬의 실행 시간은 $Theta(n\log{n})$이 될 것입니다.

예시 1. n-비트 곱셈

 분할 정복을 실제로 사용해 볼 첫 번째 예시입니다! 여러분은 주어진 n-비트 크기의 두 정수 A, B를 곱하는 연산을 수행해야 합니다.

첫 번째 방법 - A를 B번 더하기

 곱셈의 정의에 충실하여 A를 B번 더하기, 즉 덧셈 연산을 B-1번 반복합니다. 최악의 경우는 B가 n 비트를 꽉 채워 $2^n-1$가 될 때이므로, 실행시간은

\[O(2^n)\]

 입니다.

두 번째 방법 - 비트 곱셉

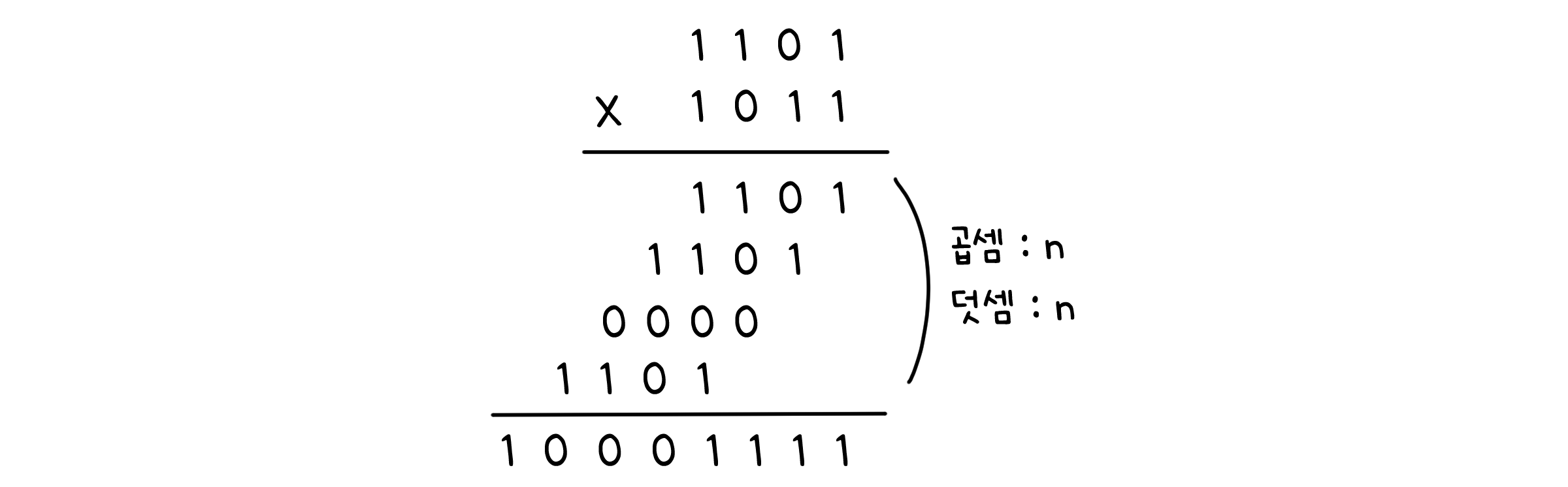
 가장 평범한 방법인 곱셈 연산을 해봅시다. B의 각 자리 수와 A를 곱하고, 이들을 모두 더합니다.

 총 n번 곱하고 n-1번 더하므로, 실행시간은

\[O(n^2)\]

 입니다.

세 번째 방법 - 분할 정복

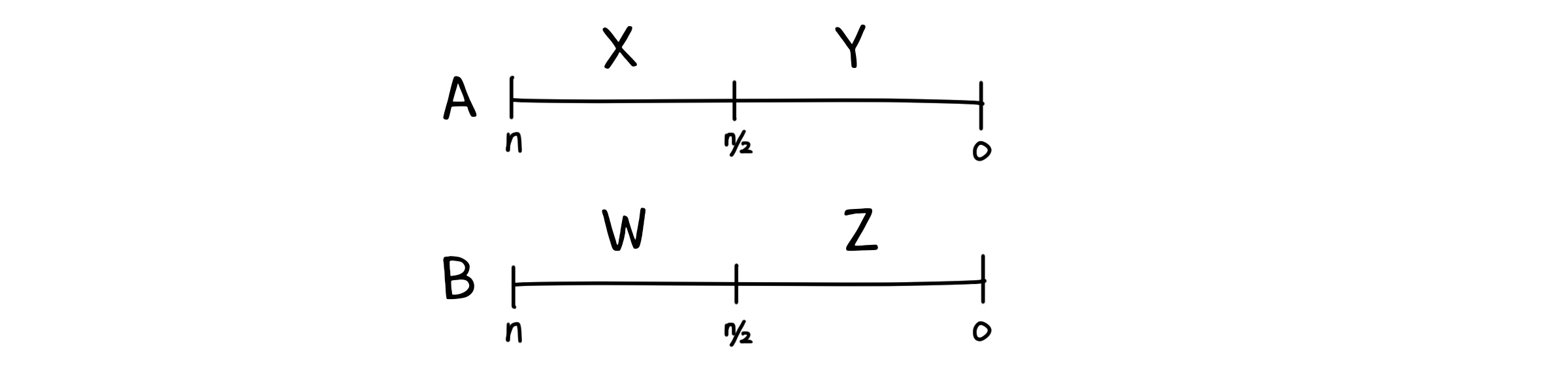
 이제 분할정복을 사용해봅시다. A와 B를 각각 절반으로 나눠 A는 XY, B는 WZ로 나타냅니다.

\[A = 2^{n/2}X + Y\] \[B = 2^{n/2}W + Z\]

 그럼 두 수의 곱 AB는 다음과 같이 나타낼 수 있겠죠.

\[AB = 2^nXW + 2^{n/2}XZ + 2^{n/2}WY + YZ\]

 AB의 곱은 n/2-비트 크기의 하위 곱셈 4개로 분할됩니다. 곱셈 외에 필요한 연산은 덧셈과 거듭제곱입니다. 덧셈은 3번, 거듭제곱은 총 $2n$번 필요하므로 $O(n)$연산이 됩니다.

2의 n 거듭제곱 연산은 단순히 비트 자리수를 n 번 이동하는 것이기 때문에 실행시간 n으로 계산합니다. 비트 연산에 대한 더 자세한 내용은 컴퓨터 시스템에서 다루겠습니다.

 따라서 실행시간은

\[T(n) = 4T(n/2) + cn\]

 마스터 정리에 따르면 $\log_2{4} = 2 > 1$이므로 다항식적으로 작은 경우이기 때문에

\[T(n) = \Theta(n^2)\]

 이 됩니다.

네 번째 방법 - 카라추바 알고리즘

 놀랍게도 여기서 실행시간을 좀 더 단축할 수 있습니다. 카라추바 알고리즘(Karatsuba algorithm)이라 불리는 이 방법은 분할과정에서 약간의 트릭을 써서 하위 문제의 분할 수를 줄였습니다.

\[AB = 2^nXW + 2^{n/2}XZ + 2^{n/2}WY + YZ\]

 기존 식에서 $2^{n/2}$를 동류항으로 하여 항들을 하나로 묶을 수 있습니다.

\[AB = (2^n - 2^{n/2})XW + 2^{n/2}XW + 2^{n/2}XZ + 2^{n/2}WY + 2^{n/2}YZ + (1 - 2^{n/2})YZ\] \[AB = (2^n - 2^{n/2})XW + 2^{n/2}(XW + XZ + WY + YZ) + (1 - 2^{n/2})YZ\] \[AB = (2^n - 2^{n/2})XW + 2^{n/2}(X + Y)(W + Z) + (1 - 2^{n/2})YZ\]

 이렇게 하면 하위문제가 세 개로 줄어듭니다! 그 크기는 여전히 n/2로 유지하면서요. 이제 식을 다시 쓰면

\[T(n) = 3T(n/2) + cn\]

 마스터 정리에 따르면 $\log_2{3} > 1$이므로 다항식적으로 작은 경우이기 때문에

\[T(n) = \Theta(n^{\log_2{3}})\]

 이 됩니다.

예시 2. 행렬 곱셈

 두 번째 예시입니다. 이번엔 정수가 아니라 $n \times n$ 크기의 두 행렬 A, B의 곱셈을 해봅시다.

이 부분은 행렬 곱셉 연산을 다룹니다. 행렬과 행렬연산에 대해 모른다면 이해가 어려울 수 있습니다!

첫 번째 방법 - 직접 계산

 다시 한 번 정의에 충실하여 요소 별로 곱한 뒤 더해봅시다.

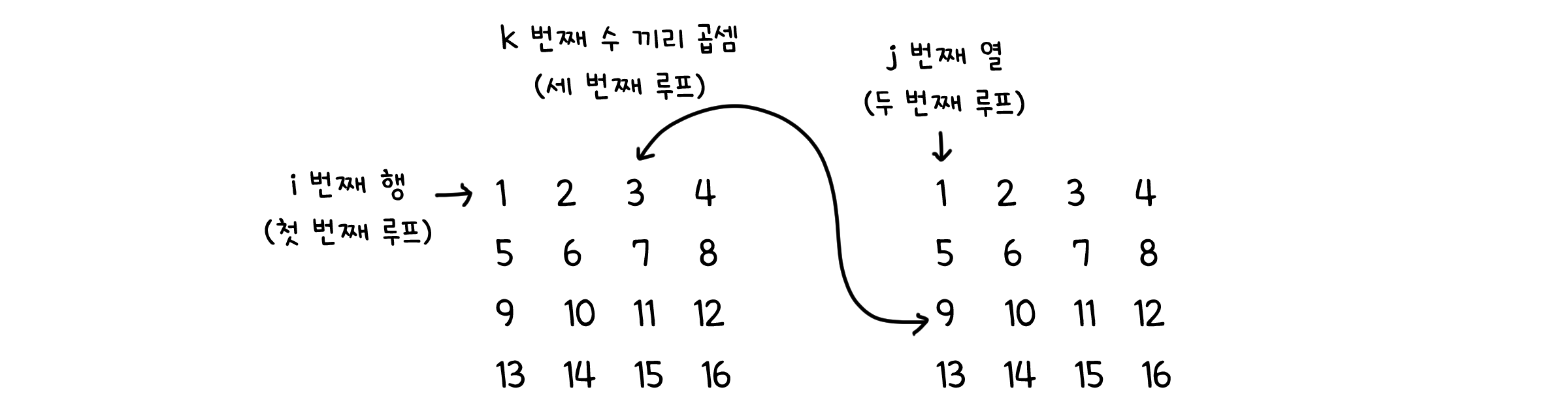
 1. A의 각 행 i에 대해 2. B의 각 열 j에 대해 3. 각 k번째 요소 마다 곱셈을 해야 하기 때문에 세 개의 반복문이 중첩되게 됩니다. 따라서 실행 시간은

\[O(n^3)\]

 입니다.

두 번째 방법 - 분할 정복

 여기서도 분할정복을 사용해봅시다. 정수 일 때는 절반으로 나누었지만 행렬은 2차원 배열이므로, A와 B를 각각 4등분으로 나눠줍니다.

 AB의 곱은 $\frac{n}{2} \times \frac{n}{2}$ 크기의 하위 행렬의 곱셈 8개로 분할됩니다. 곱셈 외에 필요한 연산은 행렬간의 덧셈입니다. 하위 행렬의 크기가 $\frac{n}{2} \times \frac{n}{2}$이므로, $\Theta(n^2)$연산이 됩니다. 따라서 실행시간은

\[T(n) = 8T(n/2) + \Theta(n^2)\]

 마스터 정리에 따르면 $\log_2{8} = 3 > 2$이므로 다항식적으로 작은 경우이기 때문에

\[T(n) = \Theta(n^3)\]

 이 됩니다.

세 번째 방법 - 슈트라센 방법

 두 수의 곱에서 약간의 꼼수를 사용했으니, 여기서도 사용할 수 있겠죠. 슈트라센의 방법(Strassen’s idea)을 소개합니다. 일단 다음과 같이 새로운 일곱 개의 행렬을 새롭게 정의합니다.

\[\begin{cases} P_1 = a(f-h) \\ P_2 = (a+b)h \\ P_3 = (c+d)e \\ P_4 = d(g-e) \\ P_5 = (a+d)(e+h) \\ P_6 = (b-d)(g+h) \\ P_7 = (a-c)(e+f) \\ \end{cases}\]

 그리고 이들을 사용해 곱 AB를 4등분한 각 부분의 결과를 계산할 수 있습니다.

\[\begin{cases} r = P_5 + P_4 - P_2 + P_6 \\ s = P_1 + P_2 \\ t = P_3 + P_4 \\ u = P_5 + P_1 - P_3 - P_7 \\ \end{cases}\]

 이렇게 하면 AB의 곱은 $\frac{n}{2} \times \frac{n}{2}$ 크기의 하위 행렬의 곱셈 7개와 덧셈 10개로 분할됩니다. 따라서 시간은

\[T(n) = 7T(n/2) + \Theta(n^2)\]

 마스터 정리에 따르면 $\log_2{7} > 2$이므로 다항식적으로 작은 경우이기 때문에

\[T(n) = \Theta(n^{\log_2{7}})\]

 이 됩니다. 덧셈 연산이 상당히 많아지긴 했지만, 그 만큼 곱셉 연산이 하나줄어들었기 때문에 싸게 먹힌 셈이죠.