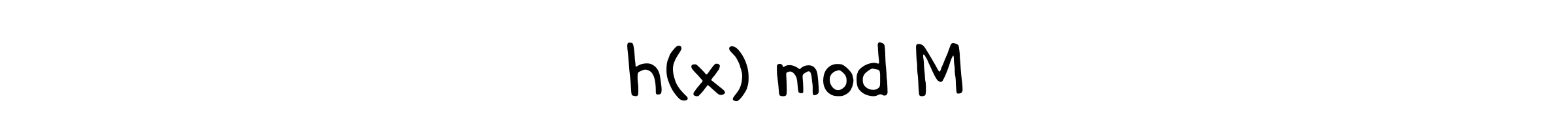[CM202] 09. 맵과 해시 테이블 (Map & Hash Table)
우리는 지금까지 다양한 형태의 ADT를 살펴보았습니다. 스택과 큐처럼 순서를 기준으로 데이터를 처리하기도 했고, 우선순위 큐에서는 우선순위에 따라 데이터를 꺼내기도 했습니다. 그런데 조금 더 직관적인 기준으로 데이터를 뽑아낼 수 있지 않을까요? 실제로 우리가 기억하는 건 데이터가 어디에 저장되어 있느냐가 아니라, 데이터가 어떤 이름으로 저장되어 있느냐일 때가 많으니까요. 이번에는 이름으로 찾는 데이터 구조, 맵 에 대해 알아보겠습니다.
맵 (Map)
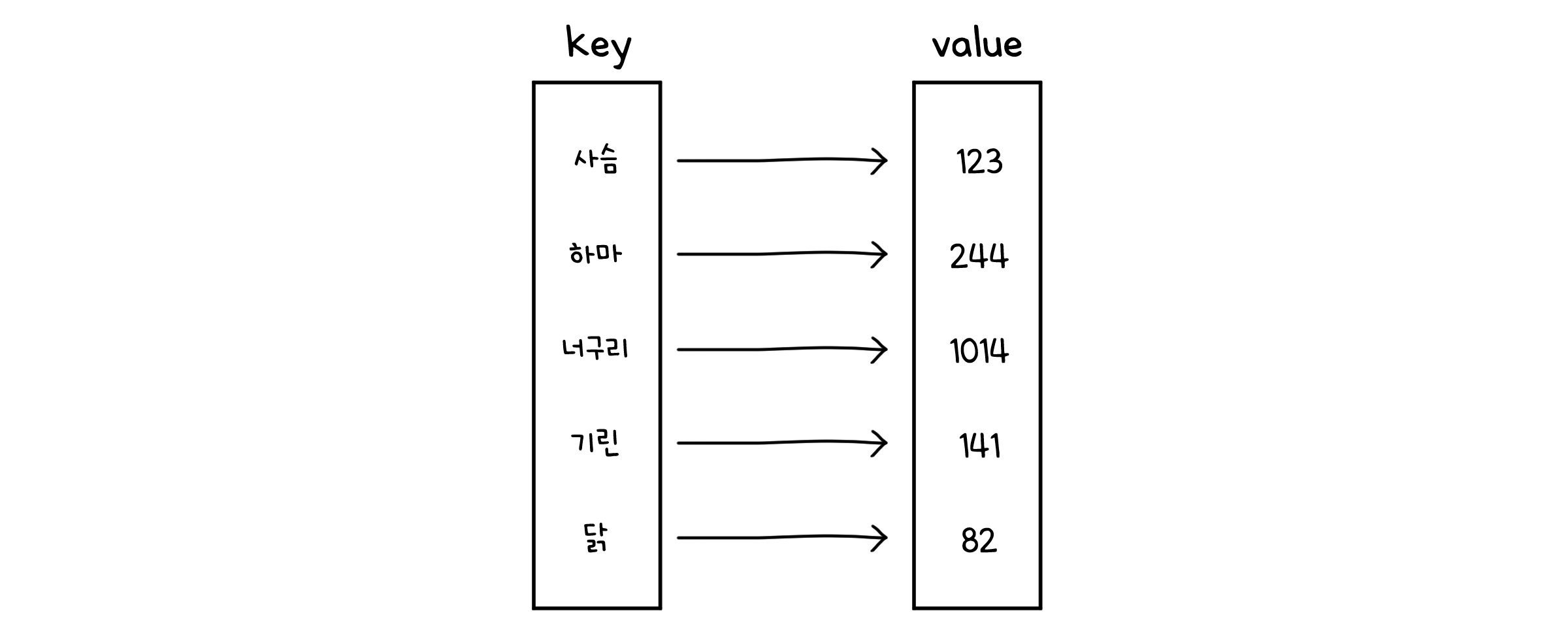
맵(Map)은 키(key)와 값(value) 쌍의 집합으로, 키를 통해 원하는 값을 빠르게 검색, 삽입, 삭제할 수 있는 구조의 ADT입니다. 일반적으로 키는 서로 중복되지 않는 고유한 값을 가지며, null과 같이 비어 있는 것을 허용하지 않습니다.
ADT: Map
맵에서 중심적으로 보아야 하는 메소드는 값을 찾는 get( ), 값을 추가(수정)하는 put( ), 그리고 값을 제거하는 remove( ) 메소드입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public interface Map<K, V> {
int size(); // 맵의 크기 반환
boolean isEmpty(); // 맵이 비어 있는지 여부 반환
V get(K k); // 키 k의 값 반환
void put(K k, V v); // 키 k에 값 v 설정
V remove(K k); // 키 k의 값 제거
Iterable<K> keySet(); // 키 목록 반환
Iterable<V> valueSet(); // 값 목록 반환
Iterable<Entry<K, V>> entrySet(); // (키, 값) 목록 반환
interface Entry<K, V> { // (키, 값) 쌍
K getKey(); // 키 가져오기
V getValue(); // 값 가져오기
}
}
이제 이 ADT를 우리가 알고 있는 데이터 구조들을 이용하여 구현할 수 있는지 하나씩 살펴봅시다.
데이터 구조: ArrayMap
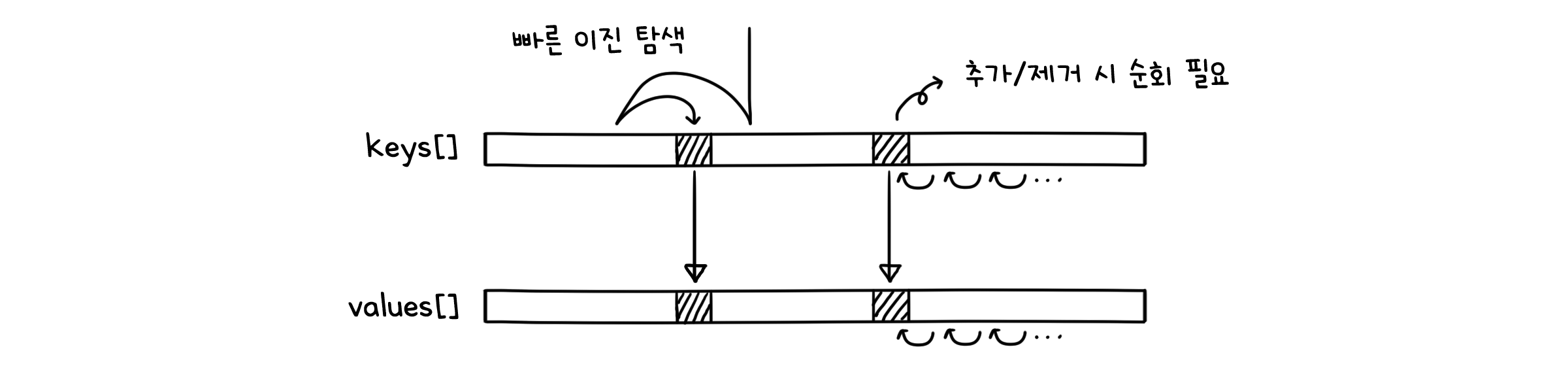
키를 저장하는 배열과 값을 저장하는 배열이 같은 위치를 공유하는 방식의 맵입니다. 이 때 키 값은 오름차순으로 정렬합니다. get( )을 실행하면 이진 탐색으로 키를 찾고, 키를 찾으면 값 배열에서 같은 인덱스의 값을 반환합니다. put( )을 실행할 때도 같은 방법으로 값을 수정합니다. 단, 키가 없다면 이진 탐색으로 찾은 인덱스 자리에 새로운 키와 값을 삽입합니다.
정렬된 배열을 사용하면 빠른 시간 안에 키에 접근할 수 있습니다. 따라서 get( ) 호출이 잦을 경우 효율적입니다. 반대로 요소를 추가하거나 제거할 때는 나머지 인덱스들을 한 칸씩 옮겨야 하기 때문에(배열 연산을 기억할 겁니다) put( )이나 remove( )연산이 비효율적입니다.
| 구현방식 | get( ) | put( ) | remove( ) |
|---|---|---|---|
| ArrayMap | $O(logn)$ | $O(n)$ | $O(n)$ |
데이터 구조: LinkedListMap
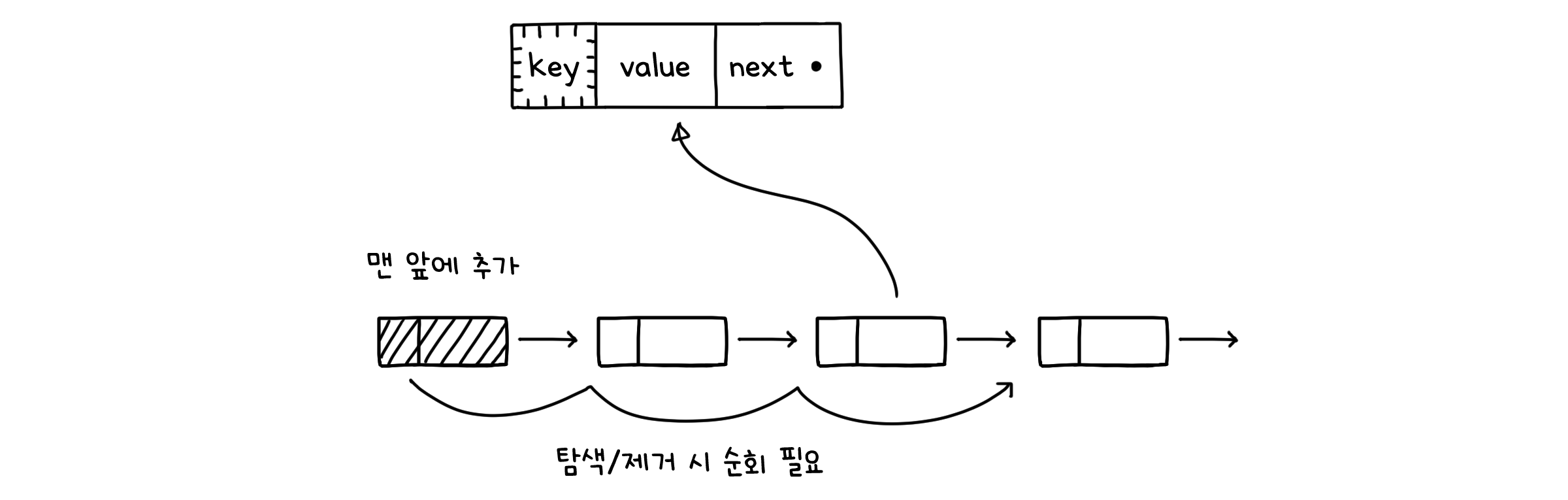
키와 값을 모두 가지는 노드들이 연결된 연결 리스트로 구현한 맵입니다. get( )을 실행하면 리스트를 순회하며 키가 있는지 찾고, 키를 찾으면 그 노드의 값을 반환합니다. put( )을 실행할 때도 같은 방법으로 노드의 값을 갱신합니다. 단, 키가 없다면 그 키를 가지는 새로운 노드를 만들어 맨 앞에 추가합니다.
ArrayMap과는 달리, 요소를 추가할 때는 노드를 맨 앞에 놓기만 해서 시간이 많이 걸리지 않습니다. 오히려 값을 찾을 때 순회를 해야 하기 때문에 시간이 오래 걸리는 편이죠. 그래서 get( )이나 remove( ) 보다는 put( ) 호출이 잦은 경우 효율적입니다.
| 구현방식 | get( ) | put( ) | remove( ) |
|---|---|---|---|
| ArrayMap | $O(logn)$ | $O(n)$ | $O(n)$ |
| LinkedListMap | $O(n)$ | $O(1)$ | $O(n)$ |
데이터 구조: HeapMap
힙은 우선도를 기반으로 정렬하는 데이터 구조이기 때문에 키를 기반으로 접근해야 하는 맵을 구현하기에는 적절하지 않아요. 만약 구현했다고 해도, 그건 맵의 키 값에 우선순위가 필요한 경우이기 때문일거에요. 맵을 구현하기에 적합한게 아니라요.
어떻게 해도 명료한 답이 나오지 않는게 이전 장의 패턴과 비슷해 보입니다. 새로운 데이터 구조를 사용해야 할 순간이라는 뜻이죠.
해시 테이블 (Hash table)
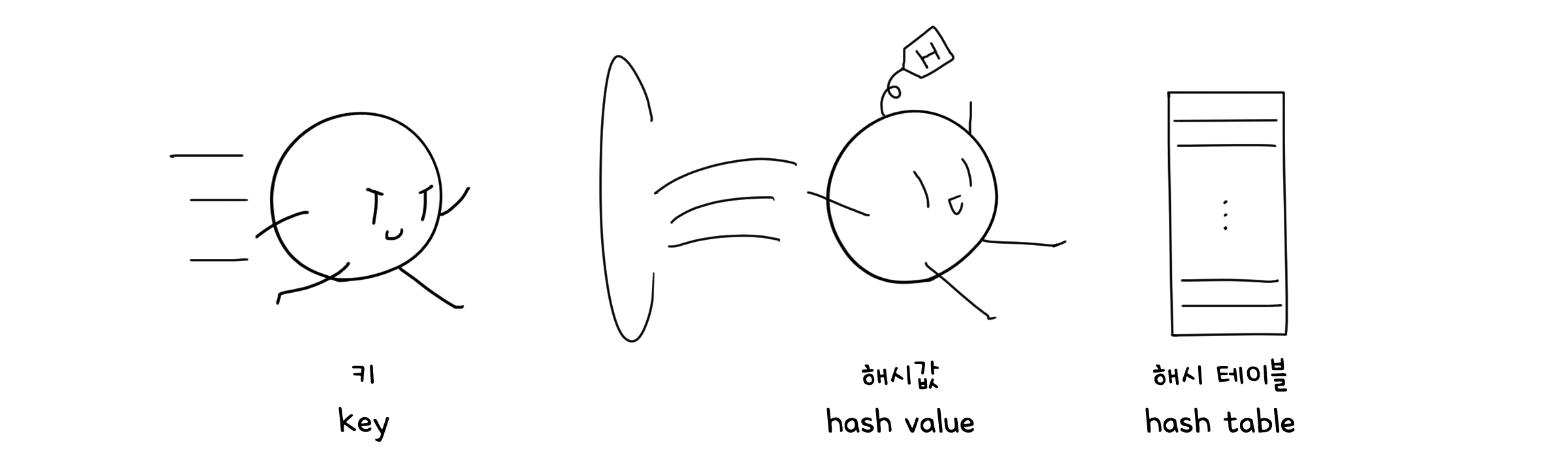
해시 테이블(Hash table)은 키에 대응하는 해시값을 배열의 인덱스로 하여 값을 저장하는 데이터 구조입니다. 해시값이 곧 키에 해당하는 셈입니다.
이 구조가 특별한 점은, 공간이나 시간적 제약이 없다는 것입니다. 자료 크기에 상관 없이 일정한 크기의 배열(해시 테이블)을 만들 수 있어 공간의 제약이 없으며, 우리가 원하는 데이터의 해시값을 알기만 하면 그 값을 인덱스로 하여 곧바로 접근할 수 있으니 시간이 제약이 없습니다.
하지만 한 가지 문제가 있다면, 서로 다른 값이 같은 해시값을 가질 수도 있다는 것입니다. 이렇게 되면 같은 인덱스에 서로 다른 두 값이 들어가야 하는 상황이 발생하죠. 이를 어떻게 해결할 것인지가 해시 테이블의 주요 논의점이 될 것입니다.
해시 함수 (Hash function)
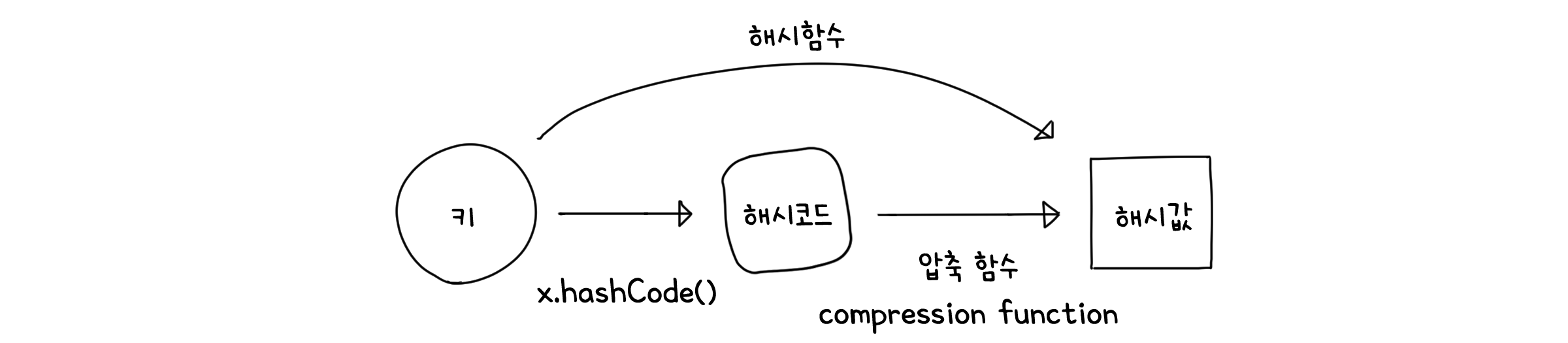
키를 해시값으로 변환하는 일련의 과정을 해시 함수(Hash function)라고 합니다. 해시 함수의 목적은 무작위로 접근하는 키들이 배열의 모든 부분에 고르게 들어가도록 인덱스 값을 만드는 것입니다. 이를 위해 해시 함수는 두 단계로 진행됩니다.
1단계: 해시 코드 (Hash code)
먼저 키 $k$를 정수 값을 가지는 해시 코드(Hash code) $h(k)$로 변환합니다. Java가 해시코드를 만드는 방법을 예로 들어보겠습니다. Java는 해시 코드를 생성하는 hashCode( )함수를 제공하는데, 일반적인 객체의 경우 그 객체의 주소값을, 실수값의 경우 해당 값에 복잡한 비트연산을 한 뒤 정수 자료형의 값으로 바꾼 형태를 반환합니다.
| 자료형 | 해시코드 |
|---|---|
| Object | 위치 주소 |
| Integer | 자기 자신 |
| Double | (int) bit XOR (bit >>> 32) |
| Boolean | 각각 true와 false에 해당하는 정수값 (미리 정해놓음) |
| String | $\sum_{i}^{n} \text{(각 문자의 아스키 코드)} \times 31^{n-i-1}$ (Horner’s method) |
2단계: 압축 함수 (Compression function)
그 다음, 해시코드는 압축 함수(Compression function)를 통해 해시 테이블 크기 만큼의 범위를 가지는 해시값으로 변환됩니다. 가장 간단한 방법은 모듈러 연산을 이용한 분할 방식(Division method)을 사용하는 것입니다. 해시 테이블의 크기가 $M$이라면 인덱스는 $0 \sim M-1$ 사이의 값을 가질테니, 해시코드를 $M$으로 나누는 것이죠.
1
2
3
private int hash(K key) {
return (key.hashCode() & 0x7fffffff) % M;
}
위의 식이 조금 지저분한 이유는 절댓값을 취했기 때문입니다. 절댓값을 취하는데
Math.abs( )함수를 사용하지 않은 이유는, 가능한 최솟값인 $-2^{31}$이 양수로 표현될 수 없기 때문입니다. 양수의 최댓값은 $2^{31}-1$이거든요. 저 식이 왜 절댓값을 취한 것인지 알기 위해서는 비트연산에 대해 알아야 합니다만, 이에 대해서는 ‘컴퓨터 시스템’에서 다루도록 하겠습니다.
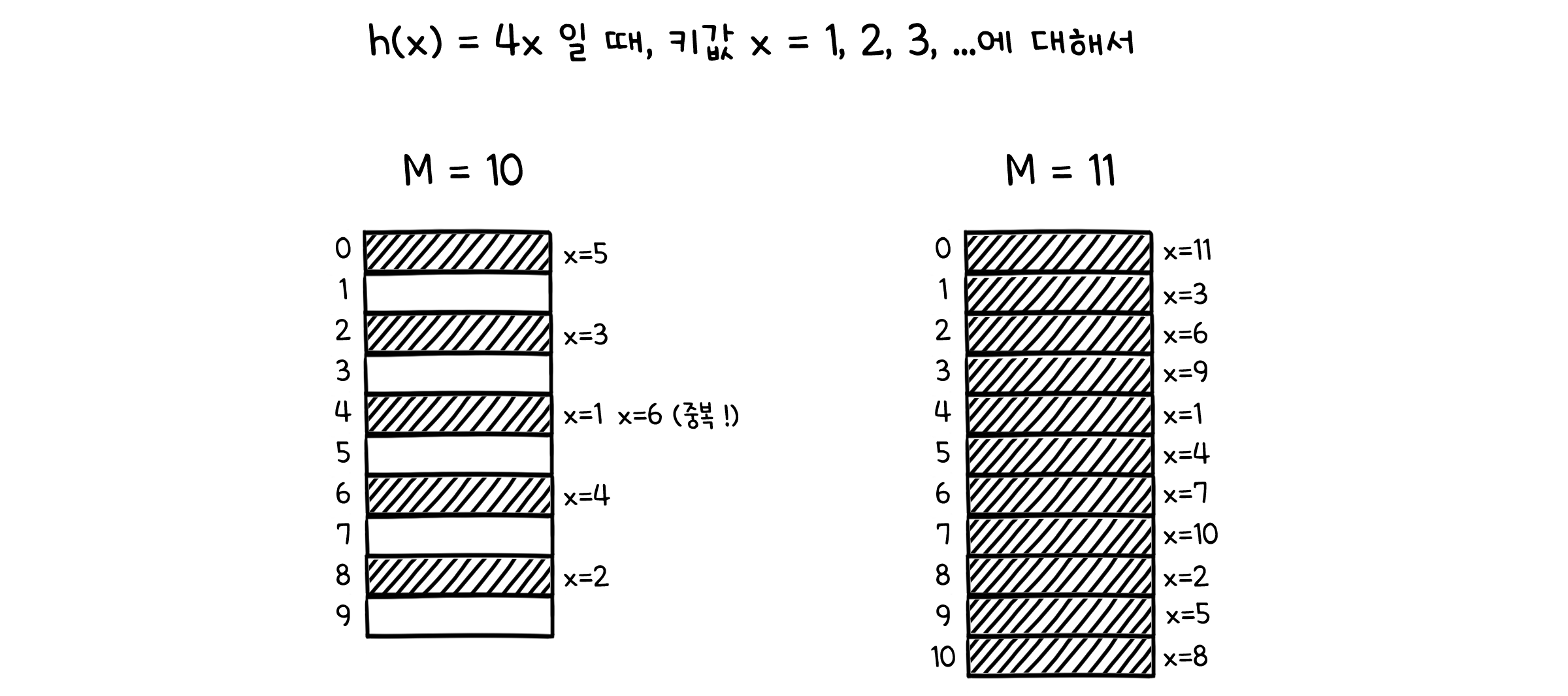
여기에 하나의 작은 팁이 있습니다. 해시 테이블의 크기를 소수(prime number)로 맞추어 놓는다면, 생성되는 해시값이 중복될 확률이 낮아집니다. 해시코드는 그 변환 방식에 따라 특정 주기를 반복하는 수들이 될 수 있습니다. 그 주기가 소수가 되는 경우는 정말 드물고요. 그러니 $0 \sim M-1$ 사이에 균일한 분포를 기대할 수 있게 됩니다.
예를 들어 어떤 값 $x$에 대해 해시코드가 $h(x) = 4x$의 연산을 통해 만들어진다고 합시다. 여기에 해시 테이블의 크기를 10으로 하여 모듈러 연산을 한다면, $x$의 값이 5만큼 차이가 날 때마다 해시값이 중복되게 됩니다. 주기가 5정도면 상당히 잦은 경우라고 볼 수 있죠. 하지만 해시 테이블의 크기가 11이라면, 테이블을 모두 채우기 전까지 중복이 발생하지 않습니다.
해시값 충돌 (Collision)
뛰어난 해시 함수를 설계하여 해시값에 중복이 없게 만든다고 해도, 키가 계속 들어온다면 언젠가 중복된 해시값이 생길 수 밖에 없습니다. 해시 테이블은 작고, 들어올 수 있는 키는 많으니까요. 이 때가 되면 우리는 정말로 이 출동에 대한 해결책을 제시해야 합니다.
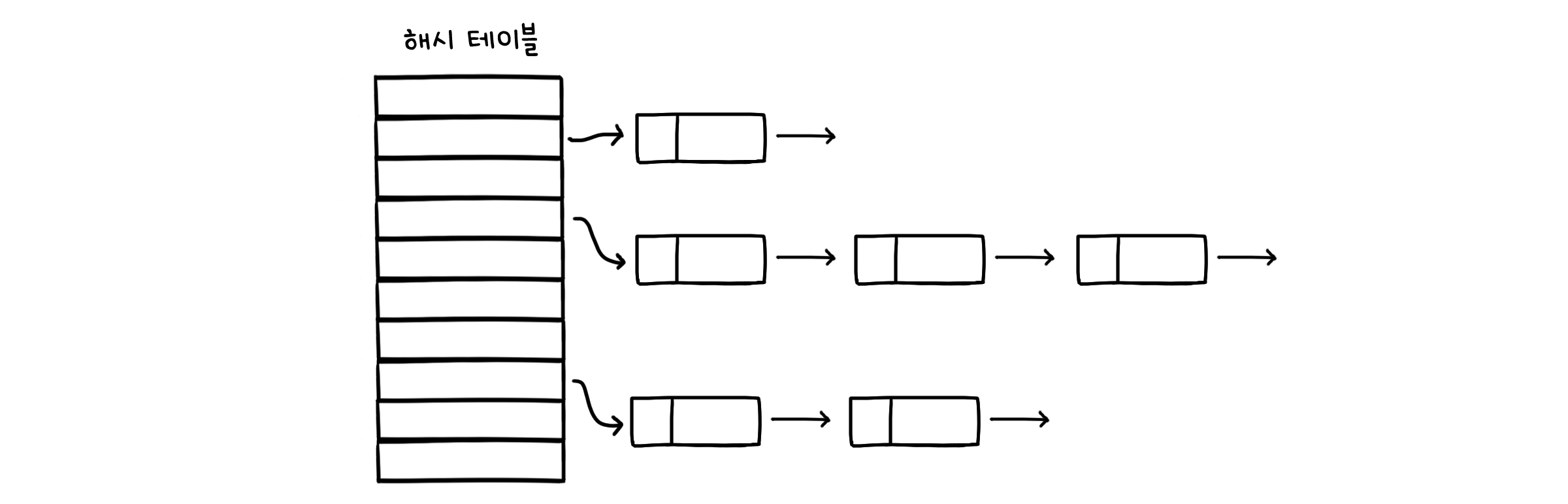
분리 연결법 (Separate chaining)
분리 연결법(Separate chaining)은 해시 테이블의 각 값을 연결 리스트로 하여 같은 해시값을 가지는 키들을 줄세우는 방법입니다. 해시 테이블의 크기가 $M$이고 키가 총 $N$개가 있다면, 연결 리스트 하나의 평균적인 길이는 $\alpha = N/M$ 만큼이 될 것입니다. 이를 해시 테이블의 부하율(Load factor)이라고 합니다. 해시 테이블은 부하율 $\alpha$를 항상 고정된 상수로 유지하도록 설계됩니다. 즉 키의 개수 $N$이 커질 때 그에 비례해서 테이블의 크기 $M$도 같이 늘어나게 됩니다.
분리 연결법의 성능은 어떨까요? 최악의 경우는 당연히 모든 키 값이 한 해시값에 몰릴 때가 되겠습니다. 그냥 하나의 연결리스트를 사용하는 맵과 다를 바가 없죠. 그러니까 유의미한 분석을 위해서, 해시 함수가 잘 만들어져 항상 키들을 해시 테이블에 고르게 분포시킨다고 가정합시다. 그렇다면 부하율에 따라 추가/제거/탐색에 걸리는 시간을 $O(1+\alpha)$로 생각할 수 있겠습니다.
| 구현방식 | get( ) | put( ) | remove( ) |
|---|---|---|---|
| ArrayMap | $O(logn)$ | $O(n)$ | $O(n)$ |
| LinkedListMap | $O(n)$ | $O(1)$ | $O(n)$ |
| SeparateChainingHashMap | $O(1)$ | $O(1)$ | $O(1)$ |
선형 탐사법 (Linear probing)
같은 칸에 줄 세우는 대신, 비어 있는 다른 자리를 찾을 수도 있습니다. 간단히 생각해 빈 자리가 나올 때 까지 한 칸씩 자리를 옮기는 것이죠.
\[[h(x) + i] \; \% \; M \quad for \; i=1, 2, 3...\]이 방법은 공간에 제약이 있기 때문에, 키의 개수 $N$이 반드시 해시 테이블의 크기 $M$보다 작아야 합니다. 성능은 어떨까요? 다시 한 번 키들이 해시 테이블에 고르게 분포된다고 가정하면, 접근하거나 제거하는데 걸리는 평균 시간은 해시 테이블의 전체 크기 $M$을 넘지 않는, $O(1)$시간이 됩니다.
| 구현방식 | get( ) | put( ) | remove( ) |
|---|---|---|---|
| ArrayMap | $O(logn)$ | $O(n)$ | $O(n)$ |
| LinkedListMap | $O(n)$ | $O(1)$ | $O(n)$ |
| SeparateChainingHashMap | $O(1)$ | $O(1)$ | $O(1)$ |
| LinearProbingHashMap | $O(1)$ | $O(1)$ | $O(1)$ |
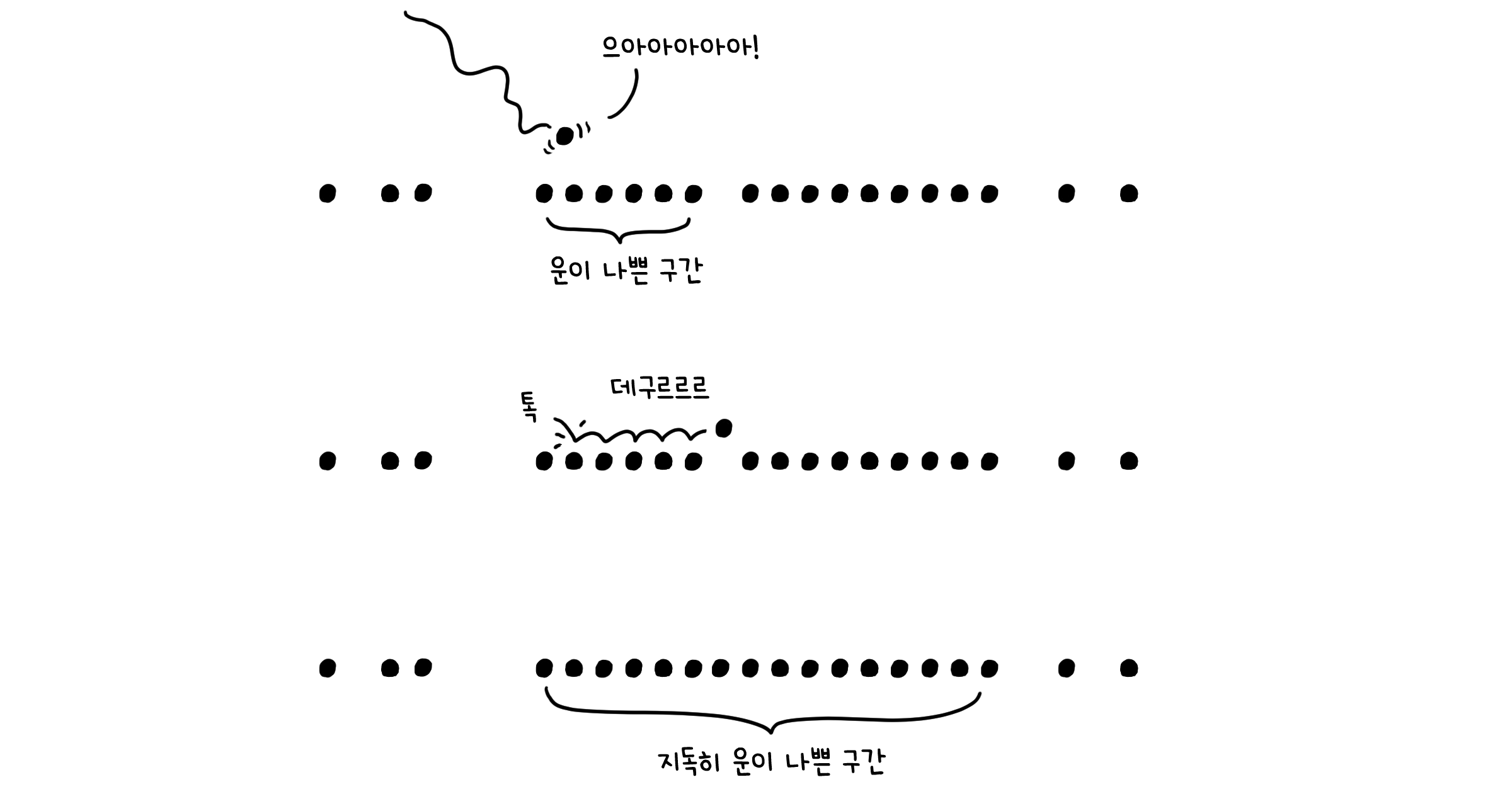
다만 선형 탐사법의 실제 성능은 해시 테이블에 키들이 얼마나 뭉쳐 있는지(Clustering)에 따라 좌우됩니다. 운이 없게 저장된 키들이 뭉쳐 있는 곳에 해시값이 할당된다면, 빈 자리가 나올 때까지 자리를 이동하는 횟수가 많아질테니까요. 최악의 경우 $O(n)$의 시간이 걸리겠죠.
변칙: 이차 탐사 (Quadratic probing)
뭉쳐져 있는 부분을 빠르게 건너뛰기 위해서는 한 번에 이동하는 양을 늘리면 됩니다. 이차 탐사법의 경우, 한 번에 이동하는 거리가 제곱으로 뛰어버립니다.
\[[h(x) + i^2] \; \% \; M \quad for \; i=1, 2, 3...\]변칙: 이중 해싱 (Double hasing)
제곱 연산을 통해서도 해시값들이 뭉쳐질 수 있습니다. 그래서 이중 해싱은 아예 이동하는 값을 불규칙하게 잡습니다. 또다른 해시 함수를 곱해서요.
\[[h(x) + i * h'(x)] \; \% \; M \quad for \; i=1, 2, 3...\]데이터 구조: SeparateChainingHashMap
분리 연결법을 이용한 해시 맵은 연결리스트를 기반으로 하여 구현할 수 있습니다. 다른 점은, 해시 테이블이 연결 리스트를 모아놓은 배열이 되어야 한다는 것입니다.
SeparateChainingHashMap - 멤버
| 이름 | 자료형 | 기본값 | 기능 |
|---|---|---|---|
| st | Node<K, V>[] | - | 연결 리스트의 배열 |
| M | int | 97 | 크기 |
| N | int | 0 | 키 개수 |
SeparateChainingHashMap - 메소드
| 이름 | 매개변수 | 반환값 | 기능 |
|---|---|---|---|
| size() | - | int | 맵의 크기 반환 |
| isEmpty() | - | boolean | 비어 있는지 여부 반환 |
| get(K k) | k : 키 | V | 키 k의 값 반환 |
| put(K k, V v) | k : 키, v : 값 | - | 키 k에 값 v 설정 |
| remove(K k) | k : 키 | V | 키 k의 값 제거 |
| keySet() | - | K[] | 키 목록 반환 |
| valueSet() | - | V[] | 값 목록 반환 |
| entrySet() | - | <K, V>[] | (키, 값) 목록 반환 |
메소드 살펴보기
get( )
1
2
3
4
5
6
7
8
9
10
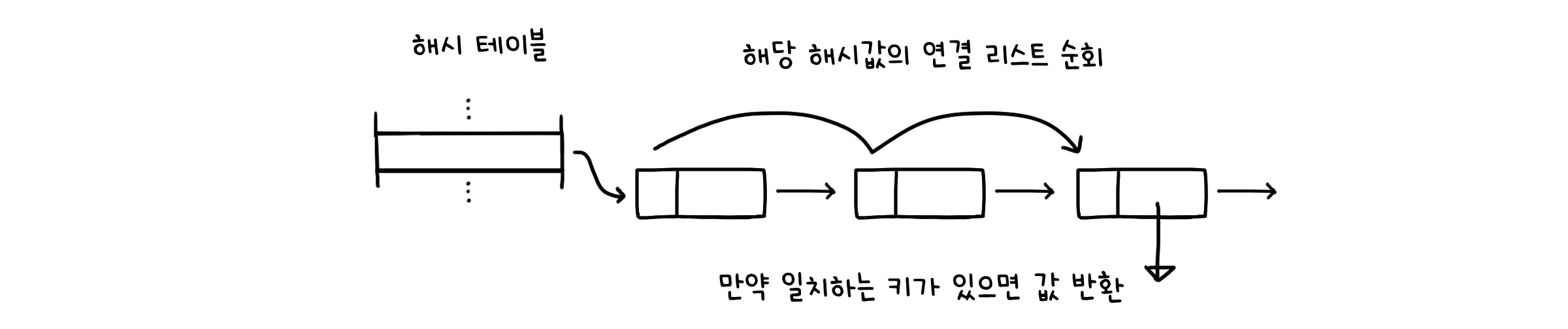
public V get(K key) {
int i = hash(key); // 해시 함수
for (Node<K, V> x = st[i]; x != null; x = x.next) { // 해당 해시값의 연결 리스트 순회
if (key.equals(x.key)) { // 만약 일치하는 키가 있으면
return (V) x.val // 값 반환
}
}
return null // 아니면 null 반환
}
put( )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
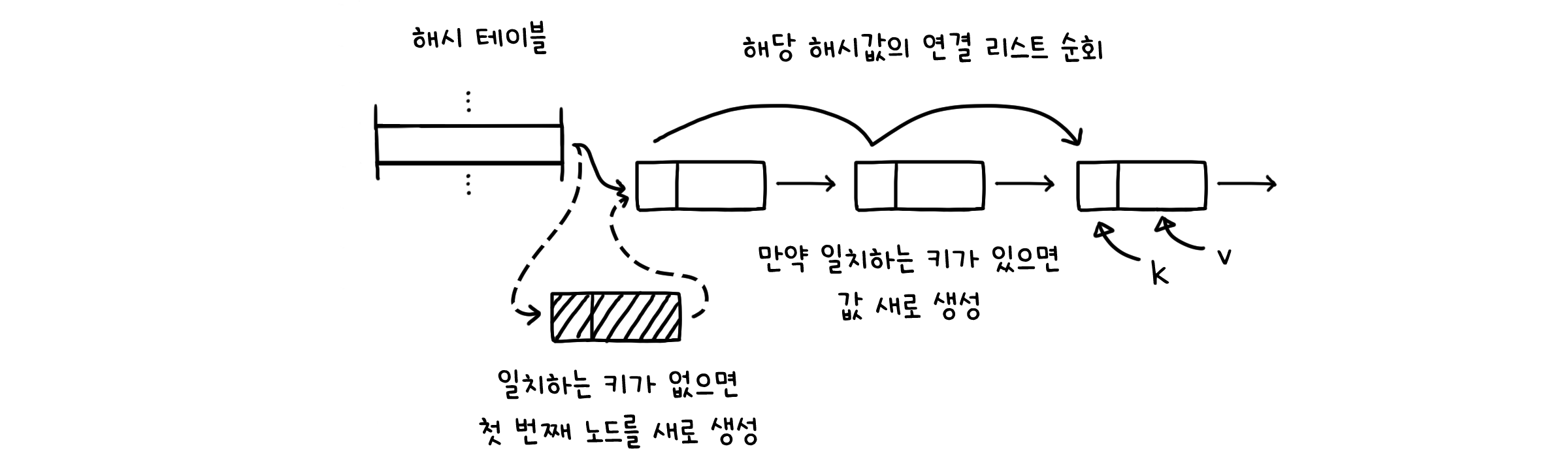
public void put(K key, V val) {
int i = hash(key); // 해시 함수
for (Node<K, V> x = st[i]; x != null; x = x.next) { // 해당 해시값의 연결 리스트 순회
if (key.equals(x.key)) { // 만약 일치하는 키가 있으면
x.val = val; // 값 새로 설정
return
}
}
// 일치하는 키가 없다면,
st[i] = new Node(key, val, st[i]); // 해당 해시값의 첫 번째 노드를 새로 생성
N++;
if (N/M >= 0.5) { // 부하율이 절반을 넘어가면
resize(2*M); // 해시 테이블 두 배 확장
}
}
remove( )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
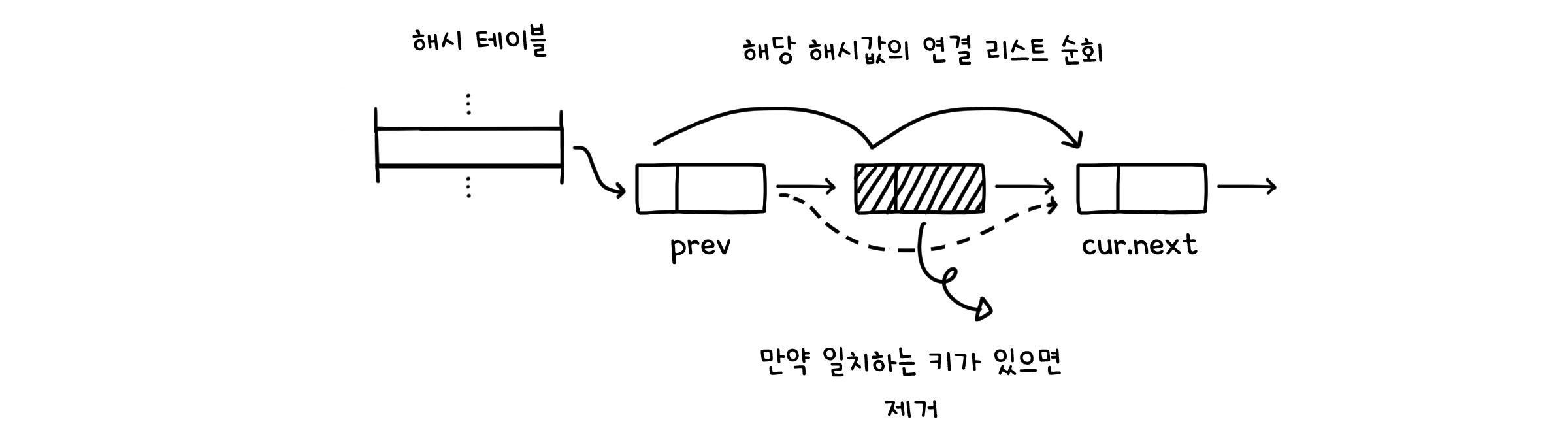
public V remove(K key) {
int i = hash(key); // 해시 함수
Node<K, V> prev = null; // 순회를 위한 이전 노드 값
Node<K, V> cur = st[i]; // 순회를 위한 현재 노드 값
while (cur != null) { // 연결 리스트 끝에 도착할 때 까지 순회
if (key.equals(cur.key)) { // 만약 일치하는 키가 있으면
if (prev == null) { // 일치하는 키가 맨 처음 노드라면
st[i] = cur.next; // 그 다음 노드를 맨 처음노드로 둠
}
else { // 맨 처음이 아니라면
prev.next = cur.next; // 현재 노드의 다음 노드를 이전 노드의 다음노드로 둠
}
N--;
if (N > 0 && N/M <= 1/8) { // 부하율이 1/8보다 작아지면
resize(M/2); // 해시 테이블 절반 감소
}
return cur.val;
}
prev = cur;
cur = cur.next;
}
return null;
}
데이터 구조: LinearProbingHashMap
선형 탐사법을 이용한 해시 맵은 키와 값의 배열을 기반으로 하여 구현할 수 있습니다.
LinearProbingHashMap - 멤버
| 이름 | 자료형 | 기본값 | 기능 |
|---|---|---|---|
| keys | K[] | - | 키 배열 |
| vals | V[] | - | 값 배열 |
| M | int | 30001 | 크기 |
| N | int | 0 | 키 개수 |
LinearProbingHashMap - 메소드
| 이름 | 매개변수 | 반환값 | 기능 |
|---|---|---|---|
| size() | - | int | 맵의 크기 반환 |
| isEmpty() | - | boolean | 비어 있는지 여부 반환 |
| get(K k) | k : 키 | V | 키 k의 값 반환 |
| put(K k, V v) | k : 키, v : 값 | - | 키 k에 값 v 설정 |
| remove(K k) | k : 키 | V | 키 k의 값 제거 |
| keySet() | - | K[] | 키 목록 반환 |
| valueSet() | - | V[] | 값 목록 반환 |
| entrySet() | - | <K, V>[] | (키, 값) 목록 반환 |
메소드 살펴보기
get( )
1
2
3
4
5
6
7
8
9
public V get(K key) {
for (int i = hash(key); keys[i] != null; i = (i+1) % M) { // 해당 해시값을 시작으로 순회
if (keys[i].equals(key)) { // 만약 일치하는 키가 있으면
return vals[i]; // 값 반환
}
}
return null; // 아니면 null 반환
}
put( )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
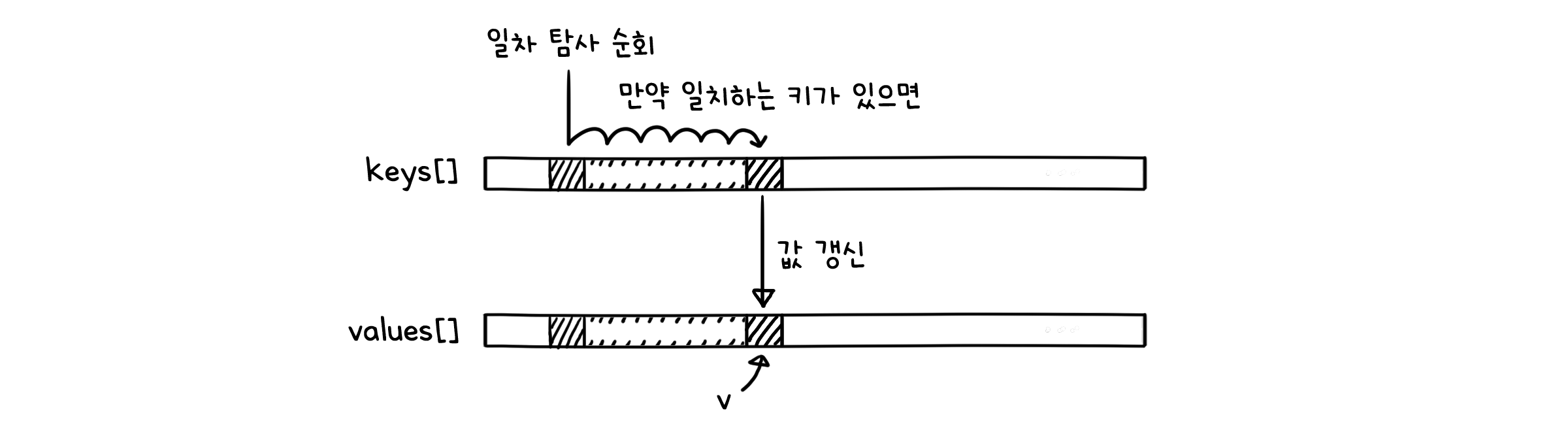
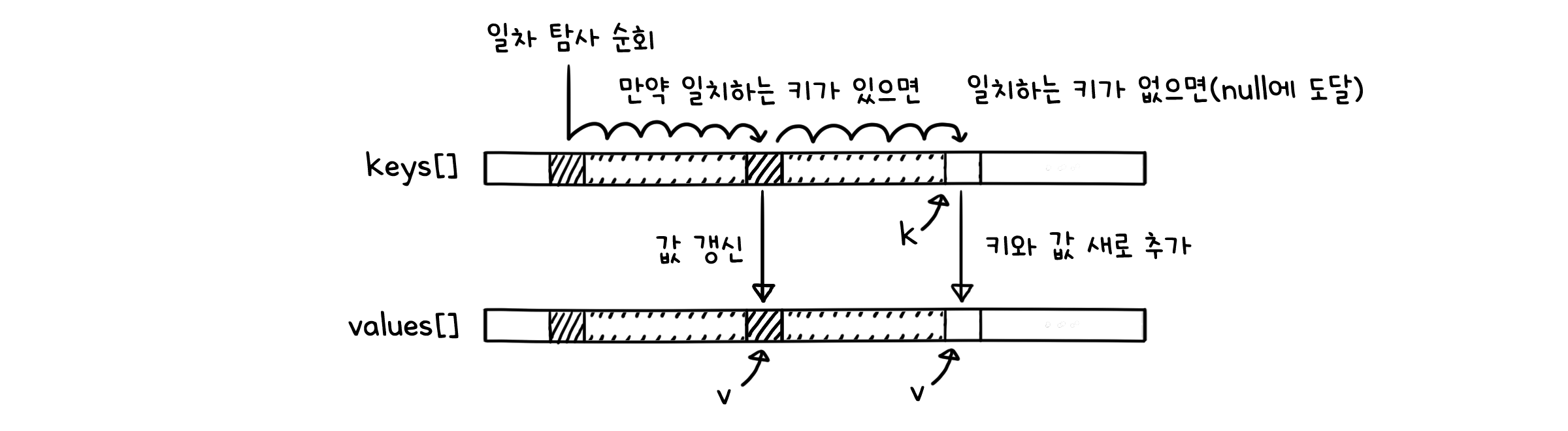
public void put(K key, V val) {
for (int i = hash(key); keys[i] != null; i = (i+1) % M) { // 해당 해시값을 시작으로 순회
if (keys[i].equals(key)) { // 만약 일치하는 키가 있으면
vals[i] = val; // 값 갱신
return;
}
}
// 일치하는 키가 없다면,
keys[i] = key; // 키 새로 추가
vals[i] = val; // 값 새로 추가
N++;
if (N/M >= 0.5) { // 부하율이 절반을 넘어가면
resize(2*M); // 해시 테이블 두 배 확장
}
}
remove( )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
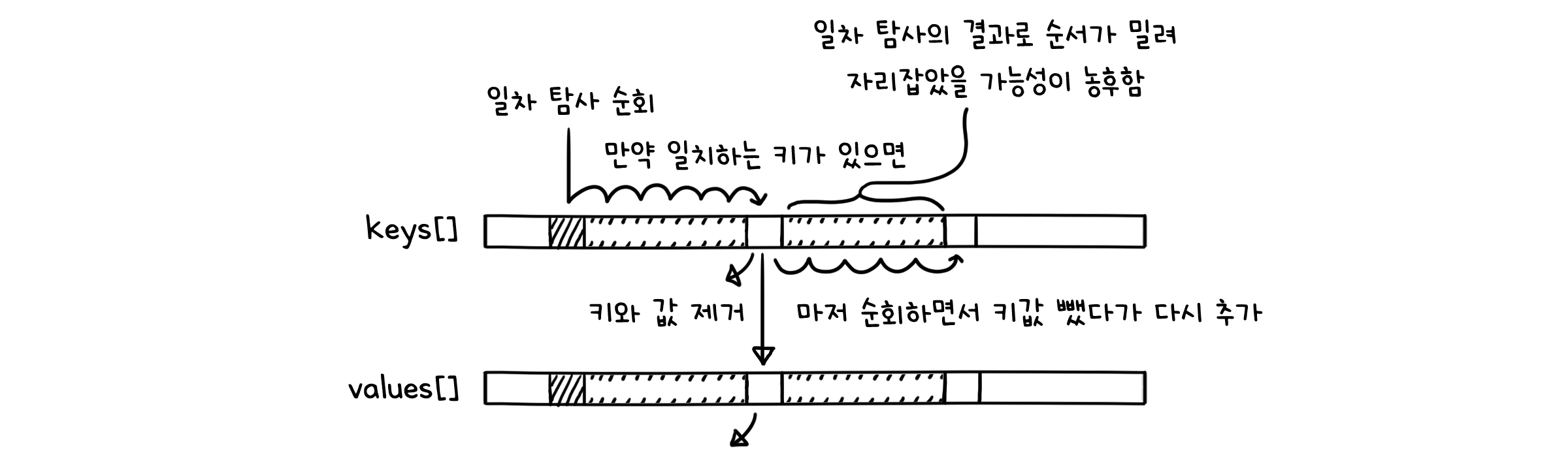
public V remove(K key) {
int i = hash(key); // 해시 함수
while (!key.equals(keys[i])) { // 해당 해시값을 시작으로 키를 찾을 때까지 순회
i = (i + 1) % m;
}
keys[i] = null; // 찾은 키 제거
vals[i] = null; // 찾은 값 제거
// 그 다음 연속해서 오는 값들을 재배치 하기
i = (i + 1) % m;
while (keys[i] != null) { // 클러스터가 끝날 때까지 순회
Key keyToRehash = keys[i];
Value valToRehash = vals[i];
keys[i] = null; // 키 제거
vals[i] = null; // 값 제거
N--;
put(keyToRehash, valToRehash); // 같은 키와 값을 다시 추가
i = (i + 1) % m;
}
N--;
if (N > 0 && N/M <= 1/8) { // 부하율이 1/8보다 작아지면
resize(M/2); // 해시 테이블 절반 감소
}
}
해시 테이블을 사용하면, 입력값의 크기와 관계없이 상수 시간 안에 값을 찾고 삽입할 수 있습니다. 그 때문에 다양한 키값을 가지는 맵 자료형을 구현하기 알맞은 형태라고 할 수 있습니다. 물론 키의 해시값들이 최소한으로 충돌한다는 가정이 있다면요.
전체 코드 보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
// interface: Map
public interface Map<K, V> {
int size();
boolean isEmpty();
V get(K k);
void put(K k, V v);
V remove(K k);
Iterable<K> keySet();
Iterable<V> valueSet();
Iterable<Entry<K, V>> entrySet();
interface Entry<K, V> {
K getKey();
V getValue();
}
}
public class SeparateChainingHashMap<K, V> implements Map<K, V> {
// nested class: Node
private static class Node<K, V> {
// member
private K key;
private V val;
private Node<K, V> next;
// constructor
public Node(K k, V v, Node<K, V> n) {
key = k;
val = v;
next = n;
}
}
// member
private Node<K, V>[] st;
private int M;
private int N;
// constructor
public SeparateChainingHashMap() { this(97); }
public SeparateChainingHashMap(int CAPACITY) {
st = (Node<K, V>[]) new Object[CAPACITY];
M = CAPACITY;
N = 0;
}
// methods
private int hash(K key) { return (key.hashCode() & 0x7fffffff) % M }
public V get(K key) {
int i = hash(key);
for (Node<K, V> x = st[i]; x != null; x = x.next) {
if (key.equals(x.key)) return (V) x.val
}
return null
}
public void put(K key, V val) {
int i = hash(key);
for (Node<K, V> x = st[i]; x != null; x = x.next) {
if (key.equals(x.key)) { x.val = val; return }
}
st[i] = new Node(key, val, st[i]);
n++;
if (N/M >= 0.5) resize(2*M);
}
public V remove(K key) {
int i = hash(key);
Node<K, V> prev = null;
Node<K, V> cur = st[i];
while (cur != null) {
if (key.equals(cur.key)) {
if (prev == null) st[i] = cur.next; else prev.next = cur.next;
N--;
if (N > 0 && N/M <= 1/8) resize(M/2);
return cur.val;
}
prev = cur; cur = cur.next;
}
return null;
}
public Iterable<K> keySet() {
java.util.ArrayList<K> list = new java.util.ArrayList<>(n);
for (int i = 0; i < M; i++)
for (Node<K, V> x = st[i]; x != null; x = x.next)
list.add(x.key);
return list;
}
public Iterable<V> valueSet() {
java.util.ArrayList<V> list = new java.util.ArrayList<>(n);
for (int i = 0; i < M; i++)
for (Node<K, V> x = st[i]; x != null; x = x.next)
list.add(x.val);
return list;
}
public Iterable<Entry<K, V>> entrySet() {
java.util.ArrayList<Entry<K, V>> list = new java.util.ArrayList<>(n);
for (int i = 0; i < M; i++)
for (Node<K, V> x = st[i]; x != null; x = x.next) {
final K k = x.key; final V v = x.val;
list.add(new Entry<K, V>() {
public K getKey() { return k; }
public V getValue() { return v; }
});
}
return list;
}
// utiliy functions
private void resize(int CAPACITY) {
SeparateChainingHashMap<K, V> temp = new SeparateChainingHashMap<K, V>(CAPACITY);
for (int i = 0; i < m; i++) {
if (keys[i] != null) { temp.put(keys[i], vals[i]); }
}
keys = temp.keys;
vals = temp.vals;
m = temp.m;
}
}
public class LinearProbingHashMap<K, V> implements Map<K, V> {
// member
private K[] keys;
private V[] vals;
private int M;
private int N;
// constructor
public LinearProbingHashMap() { this(30001); }
public LinearProbingHashMap(int CAPACITY) {
keys = (K[]) new Object[CAPACITY];
vals = (V[]) new Object[CAPACITY];
M = CAPACITY;
N = 0;
}
// methods
private int hash(K key) { return (key.hashCode() & 0x7fffffff) % M }
public V get(K key) {
for (int i = hash(key); keys[i] != null; i = (i+1) % M)
if (keys[i].equals(key))
return vals[i];
return null;
}
public void put(K key, V val) {
if (N/M >= 0.5) resize(2*M);
for (int i = hash(key); keys[i] != null; i = (i+1) % M)
if (keys[i].equals(key)) {
vals[i] = val;
return;
}
keys[i] = key;
vals[i] = val;
N++;
if (N/M >= 0.5) {
resize(2*M);
}
}
public V remove(K key) {
int i = hash(key);
while (!key.equals(keys[i])) {
i = (i + 1) % m;
}
keys[i] = null;
vals[i] = null;
i = (i + 1) % m;
while (keys[i] != null) {
Key keyToRehash = keys[i];
Value valToRehash = vals[i];
keys[i] = null;
vals[i] = null;
N--;
put(keyToRehash, valToRehash);
i = (i + 1) % m;
}
N--;
if (N > 0 && N/M <= 1/8) resize(M/2);
}
public Iterable<K> keySet() {
java.util.ArrayList<K> list = new java.util.ArrayList<>(n);
for (int i = 0; i < M; i++) if (keys[i] != null) list.add(keys[i]);
return list;
}
public Iterable<V> valueSet() {
java.util.ArrayList<V> list = new java.util.ArrayList<>(n);
for (int i = 0; i < M; i++) if (keys[i] != null) list.add(vals[i]);
return list;
}
public Iterable<Entry<K, V>> entrySet() {
java.util.ArrayList<Entry<K, V>> list = new java.util.ArrayList<>(n);
for (int i = 0; i < M; i++) {
if (keys[i] != null) {
final K k = keys[i];
final V v = vals[i];
list.add(new Entry<K, V>() {
public K getKey() { return k; }
public V getValue() { return v; }
});
}
}
return list;
}
// utiliy functions
private void resize(int CAPACITY) {
LinearProbingHashMap<K, V> temp = new LinearProbingHashMap<K, V>(CAPACITY);
for (int i = 0; i < m; i++) {
if (keys[i] != null) { temp.put(keys[i], vals[i]); }
}
keys = temp.keys;
vals = temp.vals;
m = temp.m;
}
}
![[CM202] 09. 맵과 해시 테이블 (Map & Hash Table)](/CMajor/assets/img/thumbnails/cm202/9.png)