[CM202] 08. 우선순위 큐와 힙 (Priority Queue & Heap)
잠시 기억을 몇 장 전으로 되돌려 봅시다. 첫 번째 ADT로 스택과 큐를 다룬 것이 기억날 것입니다. 스택은 나중에 들어온 것이 먼저 나가는 LIFO, 큐는 먼저 들어온 것이 먼저 나가는 FIFO 방식을 사용했어요. 이제 여기에 비선형적인 방식을 약간 곁들여, 나가는 순서를 우리 마음대로 정할 수 있게 해봅시다. 우선순위 큐에 대해 알아보겠습니다.
우선순위 큐(Priority queue)
우선순위 큐(Priority queue)는 각 요소마다 우선수위가 부여되어 높은 우선순위의 요소를 우선적으로 제거할 수 있는 구조의 ADT입니다. 이름이 큐이긴 하지만, 사실상 큐와는 전혀 다른 정책을 가지고 있는 셈이죠.
우리가 도서관이 가지고 있는 책들을 전부 조사한다고 합시다. 책장의 모든 책을 한 번에 다 꺼낼 수 있다면 좋겠지만, 애석하게도 우리에게는 작은 책 바구니 하나만 있습니다. 책을 한 권 씩 꺼내 바구니에 담아 확인할 수 밖에 없겠죠. 그리고 언젠가는 바구니에 공간이 다 차 책을 더 꺼내 담을 수 없게 될 거고요. 제일 먼저 담은 책을 빼낼 수 있겠지만, 기왕 빼는 거 제일 부피를 많이 차지하는 두꺼운 책을 꺼내는게 효율적일 수 있습니다. 그리고 새로운 책을 담는거죠. 이 경우 책의 두께가 우선순위의 기준이되는 우선순위 큐가 되는 것입니다.
요소마다 우선순위가 있다는 것에서 알 수 있듯이, 우선순위 큐의 각 요소들은 순위를 나타내는 키(key)값을 가져야 합니다. 키값이 따로 있을 수도 있고, 요소의 값 자체가 비교 가능하여 키값이 될 수도 있습니다.
ADT: MaxPriorityQueue
우선순위는 여러가지 기준이 있을 수 있습니다. 일단 여기서는 값이 클 수록 높은 우선순위를, 즉 매번 제일 큰 값이 빠져나가도록 기준을 세워보겠습니다.
1
2
3
4
5
6
7
public interface MaxPriorityQueue<K> {
int size(); // 큐의 크기 반환
boolean isEmpty(); // 비어 있는지 여부 반
K max(); // 1순위 요소 반환
void insert(K k); // 요소 추가
K delMax(); // 요소 제거 (1순위 요소)
}
MaxPriorityQueue는 최댓값을 빠르게 찾아 제거하는 것을 목적으로 하는 ADT이기 때문에, 굳이 순회를 할 필요가 없습니다. 오히려 순회를 해도 우선순위 순서를 따라 순회하도록 만들기가 어려워요. 그래서 이 인터페이스는 extends Iterable<>을 선언하지 않습니다.
MaxPriorityQueue를 구현하기 위해서 어떤 데이터 구조를 사용하면 좋을까요? 우리가 구현해야 할 핵심 기능은 요소 추가와 최댓값 제거입니다. 이 둘을 중심으로 생각해봅시다. 일반적인 정렬되지 않은 배열의 경우, 요소를 추가하는 데는 $O(1)$의 시간 밖에 걸리지 않지만 대신 최댓값을 찾는 데에는 $O(n)$의 시간이 걸립니다. 반대로 정렬된 배열은 최댓값을 찾는데 $O(1)$의 시간이 걸리지만, 요소를 추가할 때 $O(n)$의 시간이 걸리게 됩니다.
| 구현방식 | insert( ) | delMax( ) | 비고 |
|---|---|---|---|
| 정렬된 배열 & 연결 리스트 | $O(n)$ | $O(1)$ | 삽입이 느림 |
| 정렬되지 않은 배열 & 연결 리스트 | $O(1)$ | $O(n)$ | 삭제가 느림 |
비선형 구조인 이진 트리는 어떨까요? 이진 트리는 요소 추가와 최댓값 탐색 모두 $O(logn)$의 시간이 걸릴 수 있습니다. 하지만, 요소를 추가하는 과정에서 트리가 불균형하게 자라날 수 있는 위험요소가 있습니다(이건 지난 장 끝에 가볍게 언급하기도 했어요).
| 구현방식 | insert( ) | delMax( ) | 비고 |
|---|---|---|---|
| 정렬된 배열 & 연결 리스트 | $O(n)$ | $O(1)$ | 삽입이 느림 |
| 정렬되지 않은 배열 & 연결 리스트 | $O(1)$ | $O(n)$ | 삭제가 느림 |
| 이진 트리 (BST) | $O(logn)$ | $O(logn)$ | 불균형 가능성 있음 |
이때까지 다루었던 데이터 구조로는 이상적인 구현을 할 수 없을 것 같습니다. 뭔가 비선형적이면서도 변칙성이 없는, 새로운 데이터 구조가 필요해 보입니다.
힙 (Heap)
힙(Heap)은 이진 트리를 기반으로 하여, 모든 노드에 대해 부모-자식 간 대소 관계가 일관된 자료 구조입니다. 말이 조금 어려운데 풀어서 설명 하자면, 어떤 노드이던, 부모 노드가 자식노드보다 순서 상 우위(클 수도, 작을 수도 있죠)에 있다는 것입니다.
힙은 완전 이진 트리(Complete binary tree)의 형태로 표현할 수 있어야 합니다. 완전 이진 트리는 루트부터 맨 밑 층까지, 맨 밑 층에서는 왼쪽 끝에서부터 차례대로 노드가 전부 채워진 상태를 말합니다. 이 때문에 이진 힙(Binary heap)이라고 부르기도 합니다.
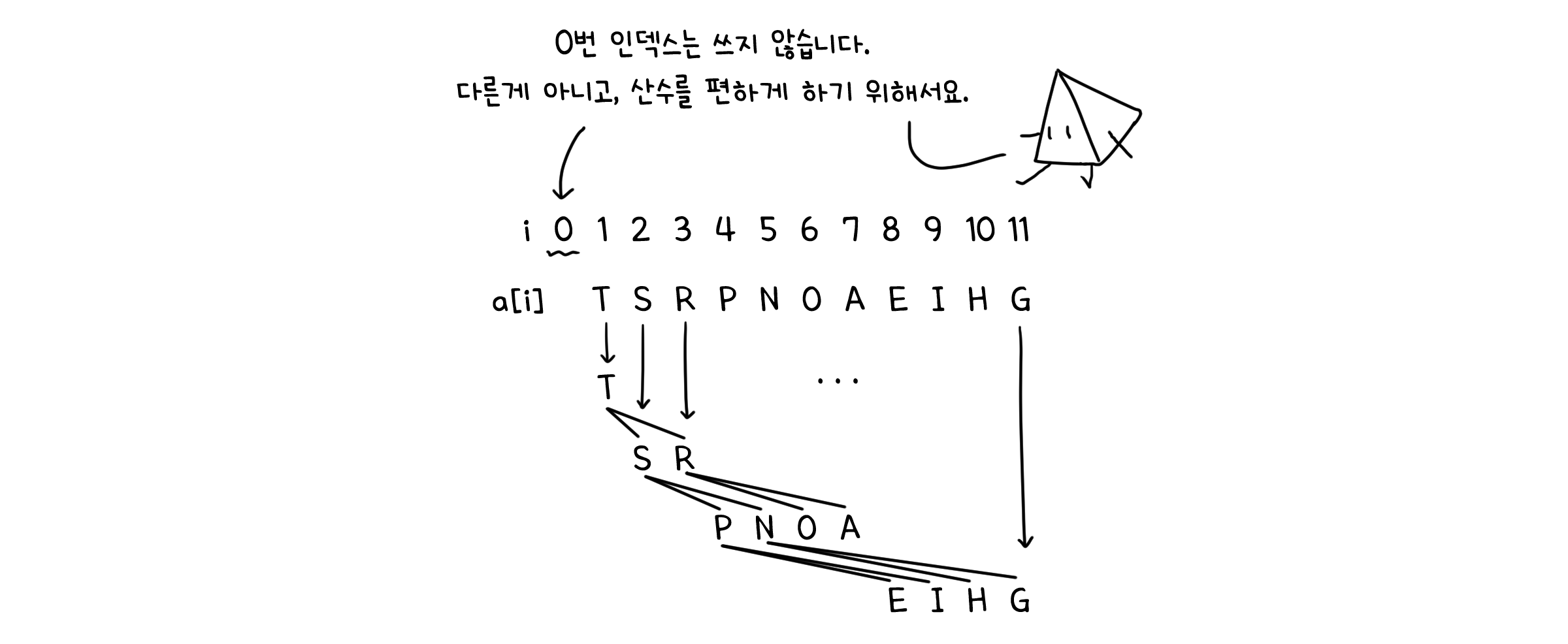
‘표현할 수 있어야’한다고 했듯이, 힙은 반드시 트리의 형태로 존재하는 것이 아닙니다. 각 요소에 번호를 매겨, 배열의 형태로 저장할 수도 있다는 것이죠. 이 경우 $k$번 노드의 부모는 $k/2$번으로, 자식은 $2k$와 $2k+1$으로 접근할 수 있습니다.
힙 복원하기 (Reheapifying)
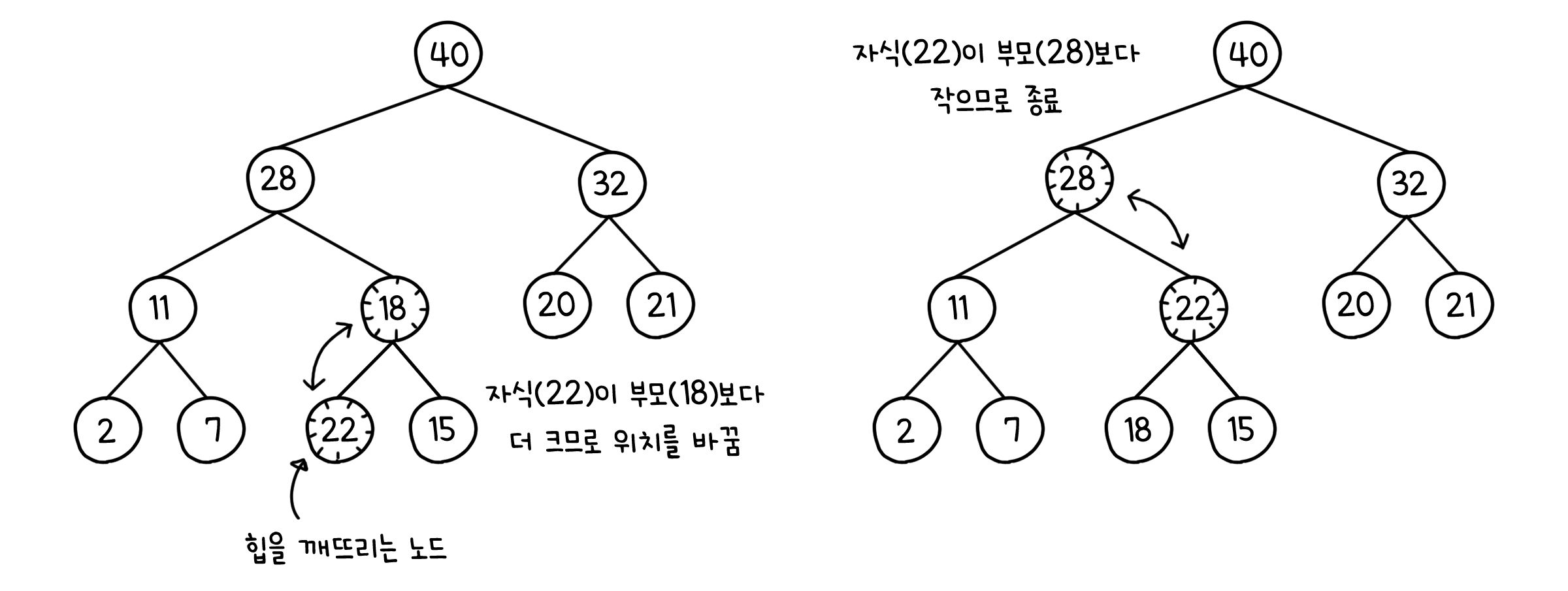
완벽히 정렬된 힙에 새로운 요소를 하나 추가하면 곧 정렬이 깨지게 됩니다(정말정말 우연히 정렬 조건을 만족하는 값이 들어가는게 아니라면요). 그러면 정렬 조건을 만족하게 만들어 다시 힙을 복구해야 합니다. 새로 들어온 값을 알맞은 자리로 옮겨서 말이죠. 이를 힙 복구(Reaheapifying)이라고 합니다.
아래에서 위로 - swim
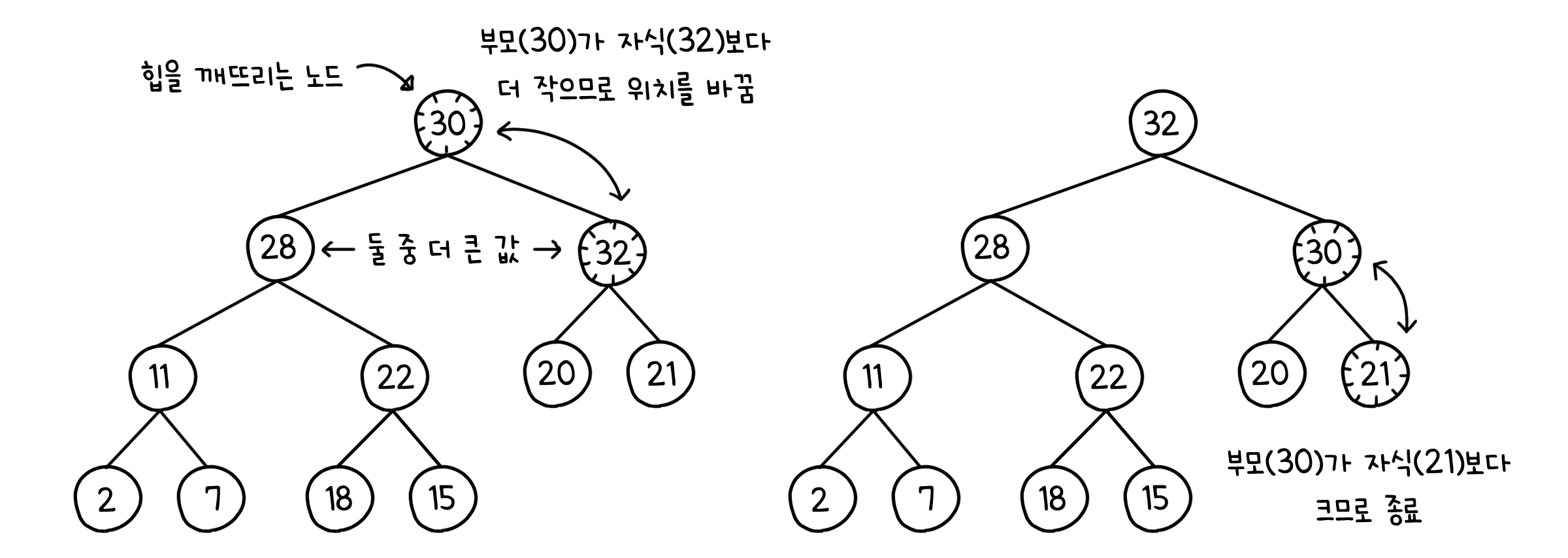
아래에 있던 노드가 정렬을 위해 위로 올라가는 과정입니다. $k$번째 노드의 부모는 $k/2$번째 노드이므로, 둘을 비교하여 $k$번째의 값이 더 크다면 서로 위치를 바꿉니다. 형제 노드간의 대소관계는 고려하지 않아도 되기 때문에 $k$번째의 옆에 있던 형제 노드와 $k/2$번째에 있던 노드를 비교할 필요는 없습니다. 이렇게 노드는 자신의 부모 값보다 더 작거나 루트에 도달할 때까지 계속 위로 올라갑니다.
위에서 아래로 - sink
위에 있던 노드가 정렬을 위해 아래로 내려가는 과정입니다. $k$번째 노드의 자식은 $2k$와 $2k+1$번째 노드입니다. 올라갈때와는 달리 비교할 노드가 최대 둘 이므로, 두 자식 중 더 큰 값을 $k$번째 노드와 비교합니다. $k$번째의 값이 더 크다면 서로 위치를 바꿉니다. 역시 형제 노드간의 대소관계는 고려하지 않아도 됩니다. 이렇게 노드는 자신의 자식 둘 보다 크거나 힙 크기를 벗어날 때까지 계속 아래로 내려갑니다.
데이터 구조: MaxPQ
이제 이진 힙 데이터 구조를 이용해 우선순위 큐를 구현할 수 있을 것입니다. 이진 탐색 트리때와 같이 힙의 값(key) 또한 서로 비교가 가능한 자료형이어야겠죠.
1
2
3
4
5
6
7
8
9
10
11
12
13
// java에서 Comparable<E>은 java.lang.Comparable 에 미리 구현되어 있습니다.
public interface Comparable<E> {
int compareTo(E other); // (자기자신 - other)의 결과값을 반환.
// 결과값 < 0 : 자기자신 < other
// 결과값 = 0 : 자기자신 < other
// 결과값 > 0 : 자기자신 > other
}
// K는 비교 가능해야 함 //
public class MaxPQ<K extends Comparable<K>> implements MaxPriorityQueue<K> {
// ...
}
MaxPQ - 멤버
| 이름 | 자료형 | 기본값 | 기능 |
|---|---|---|---|
| pq | K[] | - | 우선순위 큐 |
| n | int | 0 | 크기 |
MaxPQ - 메소드
| 이름 | 매개변수 | 반환값 | 기능 |
|---|---|---|---|
| size() | - | int | 큐의 크기 반환 |
| isEmpty() | - | boolean | 비어 있는지 여부 반환 |
| max() | - | K | 1순위 요소 반환 |
| insert(K k) | k : 요소 | - | 요소 추가 |
| delMax() | - | K | 요소 제거 |
| sort() | - | - | 힙 정렬 |
MaxPQ - 보조함수
MaxPQ의 메소드를 구현하기 위해 필요한 보조함수들이 많습니다. 따로 모아서 미리 살펴보겠습니다.
| 이름 | 매개변수 | 반환값 | 기능 |
|---|---|---|---|
| resize(int n) | n : 재설정 크기 | - | 힙의 크기를 n으로 재설정 |
| less(K v, K w) | v : 요소1, w : 요소2 | boolean | v가 w보다 작은지 확인 |
| exch(K[] a, int i, int j) | a : 배열, i : 위치1, j : 위치2 | 배열 a에서 i번째와 j번째를 교환 | |
| swim(K k) | k : 요소 | - | 요소를 위로 이동시켜 정렬 |
| sink(K k) | k : 요소 | - | 요소를 밑으로 이동시켜 정렬 |
resize( )
1
2
3
4
5
private void resize(int n) {
K[] temp = (K[]) new Comparable[n];
for (int i = 1; i <= n; i++) { temp[i] = pq[i]; } // n 크기의 배열을 만들어 복사
pq = temp; // pq가 새로운 배열을 가리키도록 함
}
less( )
1
2
3
private static boolean less(K v, K w) {
return v.compareTo(w) < 0 // v가 w보다 작으면 참을 반환
}
exch( )
1
2
3
4
5
private static void exch(K[] a, int i, int j) {
K swap = a[i]; // i번째 요소 저장
a[i] = a[j]; // i번째 요소의 값을 j번째 요소 값으로
a[j] = swap; // j번째 요소의 값을 저장했던 값으로
}
이제 less( )와 exch( )를 이용해 reheapifying 함수들을 구현할 수 있습니다.
swim( )
1
2
3
4
5
6
private void swim(int k) {
while (k > 1 && less(k/2, k)) { // 첫 번째(루트)이거나 부모보다 작아질 때까지
exch(k, k/2); // 자신(k)과 부모(k/2) 자리를 교환
k = k/2; // 위치 갱신
}
}
sink( )
1
2
3
4
5
6
7
8
9
10
11
12
13
private void sink(int k) {
while (2*k <= n) { // 힙의 크기를 벗어날 때까지
int j = 2*k;
if (j < n && less(j, j+1)) { // 만약 오른쪽(2k+1)이 왼쪽(2k)보다 더 크면
j++; // 오른쪽 선택
}
if (!less(k, j)) { // 자신이 자식보다 더 크면
break; // 종료
}
exch(k, j); // 자신(k)과 자식(2k or 2k+1) 자리를 교환
k = j; // 위치 갱신
}
}
메소드 살펴보기
이제 resize( )와 swim( ), 그리고 sink( )를 이용해 메소드들을 구현할 수 있습니다.
insert( )
1
2
3
4
5
6
7
8
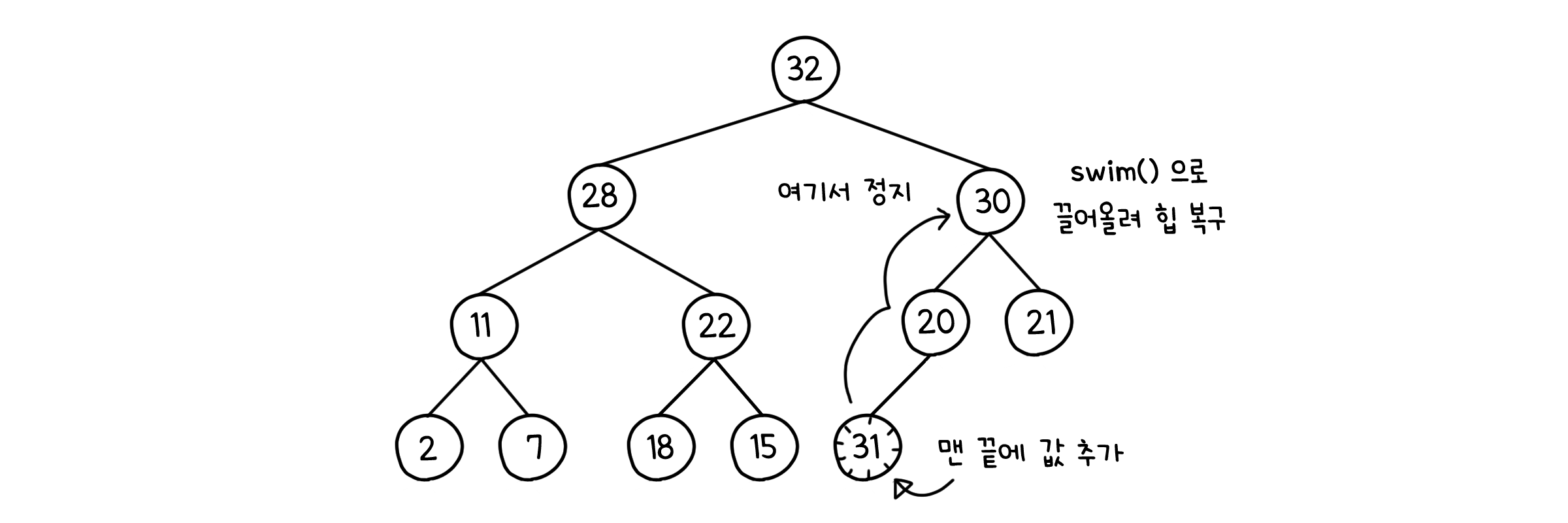
public void insert(K k) {
if(n == pq.length - 1) { // 힙의 공간이 다 찼다면
resize(2 * pq.length); // 두 배 전략: 크기를 두 배 증가
}
pq[++n] = k; // 맨 끝에 값 추가
swim(n); // n번째 노드를 끌어 올려 힙 복구
}
delMax( )
1
2
3
4
5
6
7
8
9
10
11
12
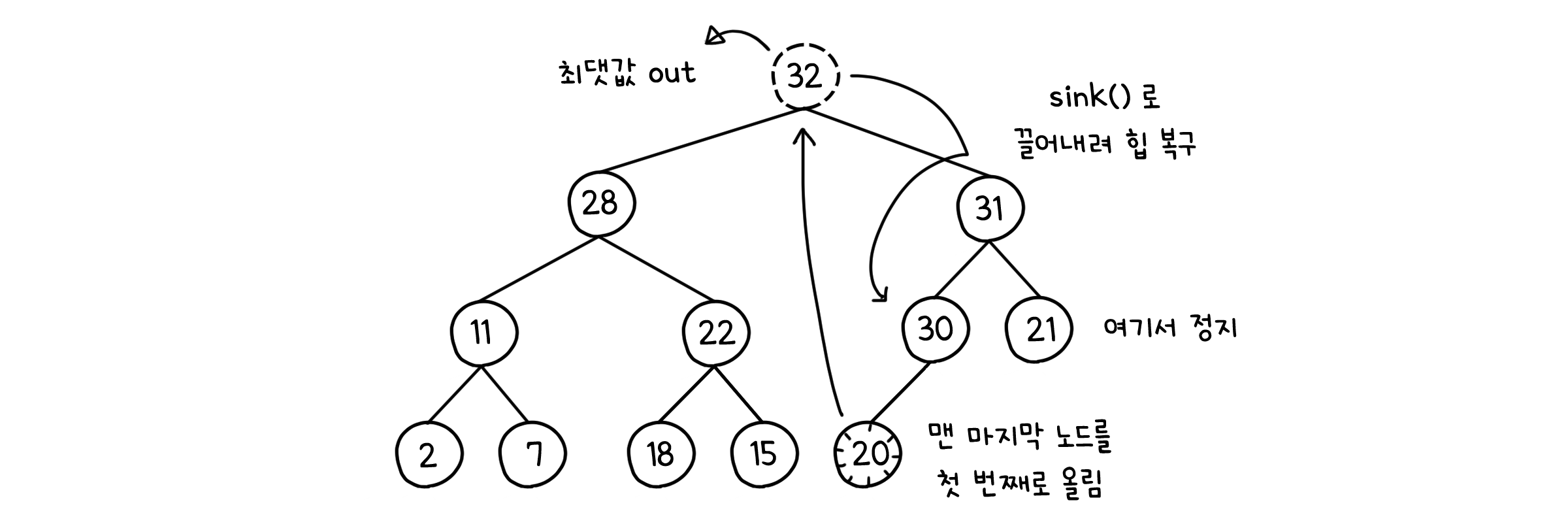
public K delMax() {
K max = pq[1]; // 첫 번째(루트) 노드 저장
exch(1, n--); // 맨 마지막 노드를 첫 번째로 올리고 크기 한 칸 감소
sink(1); // 첫 번째 노드를 끌어 내려 힙 복구
pq[n+1] = null; // 마지막 노드 자리는 비움
if ((n > 0) && (n == (pq.length - 1) / 4)) { // 힙의 공간 중 1/4만 차지한다면
resize(pq.length / 2); // 절반 전략: 크기를 절반 감소
}
return max;
}
이진 힙을 사용한 우선순위 큐는 다른 선형적인 구조와 비교해서 안정적인 계산 성능을 보입니다. swim( ) 또는 sink( )를 통해 계산하게 되는 횟수는 노드의 깊이를 넘지 않고, 완전 이진 트리이기 때문에 어디서든 깊이의 최대값은 $logn$으로 같기 때문입니다. 따라서 모든 경우에 대해 일관적으로 $O(logn)$의 시간이 걸리게 되죠. 이 덕분에 이진 힙은 우선순위 큐를 효율적으로 구현하는 핵심 자료구조로 사용됩니다.
| 구현방식 | insert( ) | delMax( ) | 비고 |
|---|---|---|---|
| 정렬된 배열 & 연결 리스트 | $O(n)$ | $O(1)$ | 삽입이 느림 |
| 정렬되지 않은 배열 & 연결 리스트 | $O(1)$ | $O(n)$ | 삭제가 느림 |
| 이진 트리 (BST) | $O(logn)$ | $O(logn)$ | 불균형 가능성 있음 |
| 이진 힙 (신규!) | $O(logn)$ | $O(logn)$ | 불균형 가능성 없음 |
우선순위 큐 써 먹기 - 힙 정렬 (Heap sort)
결국 우선순위 큐는 매번 우선순위에 따라 요소들을 정렬시킨 후, 맨 첫 번째 요소를 빼가는 원리였습니다. 그 말은, 이 큐 구조 자체를 정렬에 써 먹을 수도 있다는 뜻이죠! 이를 힙 정렬(Heap sort)이라고 합니다.
힙 정렬의 과정은 두 단계로 이루어집니다.
무작위로 정렬된 배열을 힙으로 만든다
최댓값을 빼서 맨 뒤로 보내는 것을 반복한다.
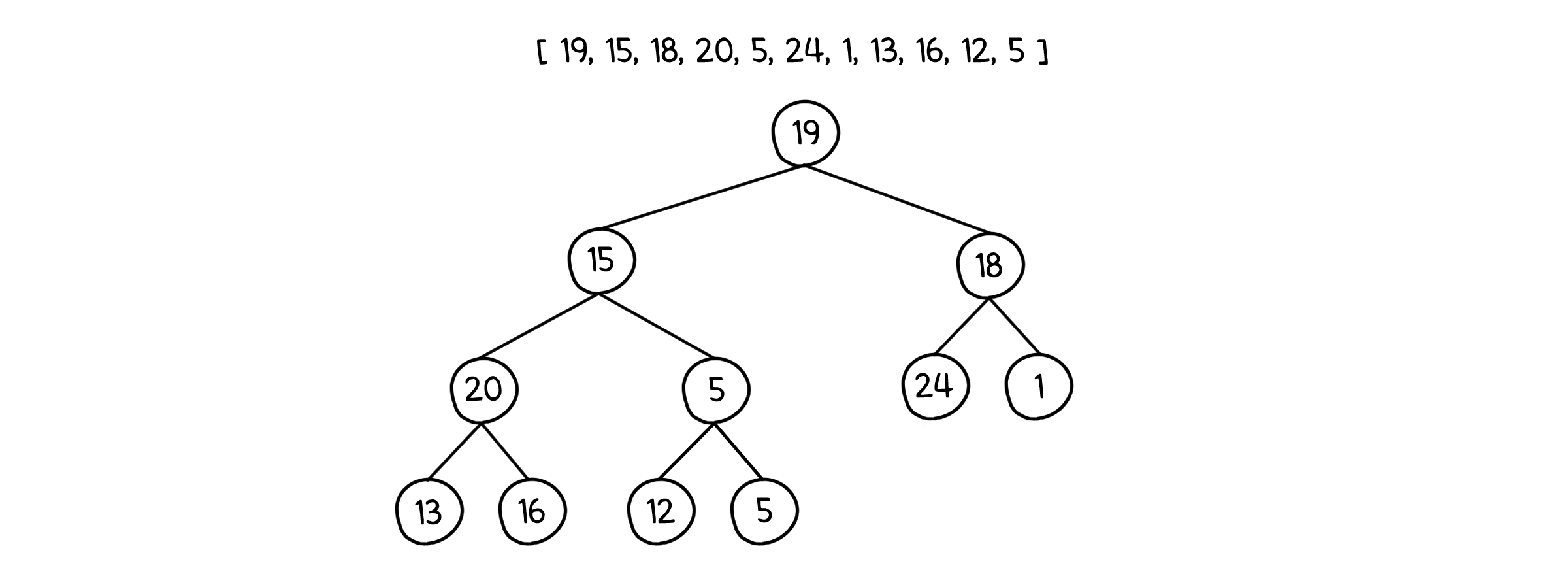
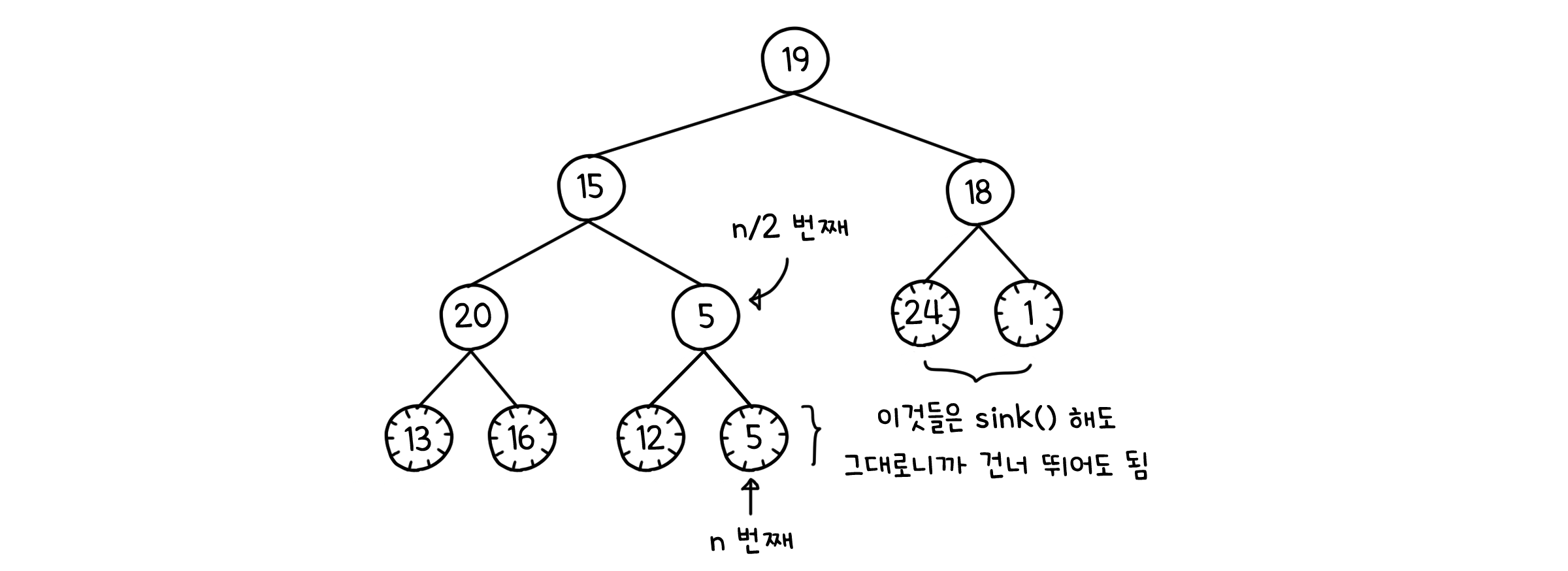
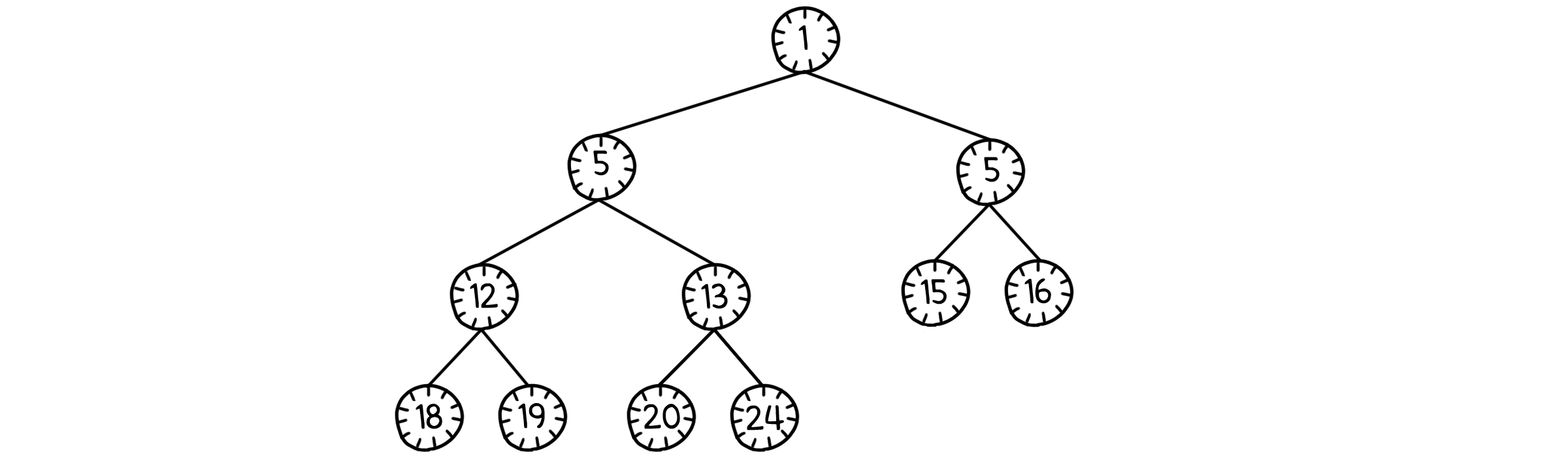
과정을 좀 더 자세히 알아보기 위해 예를 들어봅시다. 우선 무작위 배열을 보기 쉽게 완전 이진 트리로 나타내 보았습니다.
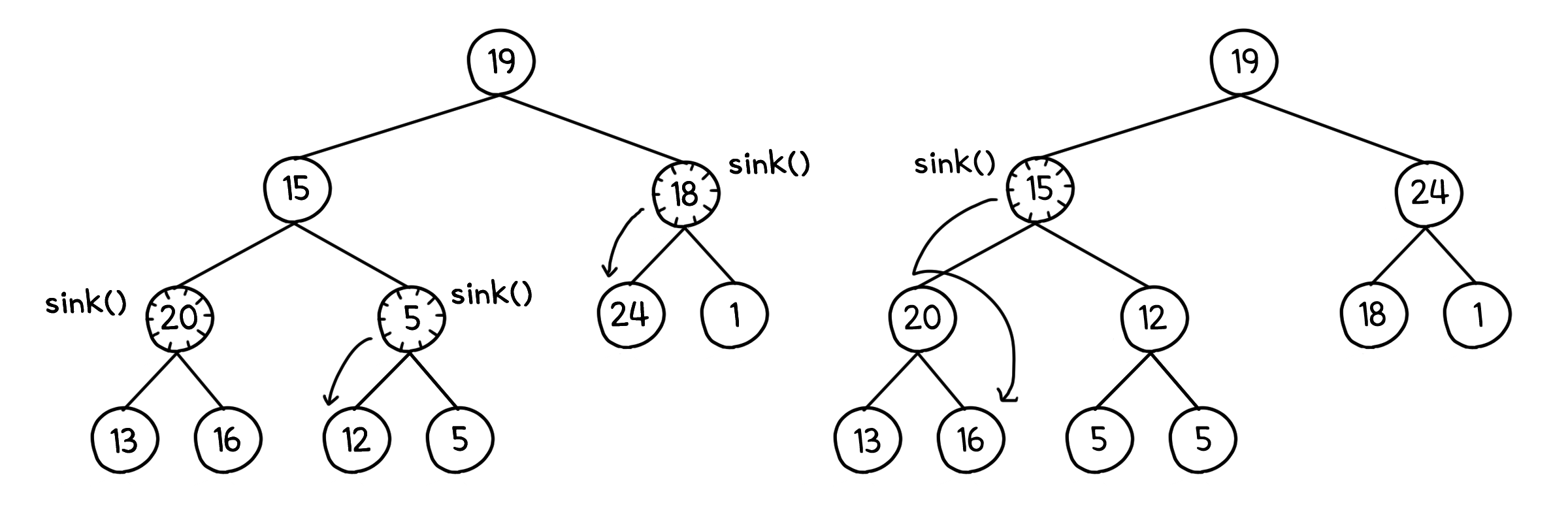
이제 이 배열을 힙으로 만들어야 합니다. 이를 위해 밑에서부터 하나씩 sink( )를 돌려줍시다. 이 때 잎 노드의 하위 힙은 어차피 높이가 1이니 sink( )를 돌리는 의미가 없을 것입니다. 그러니 힙의 절반, 그러니까 $n/2$번째 노드부터 시작해도 문제 없습니다.
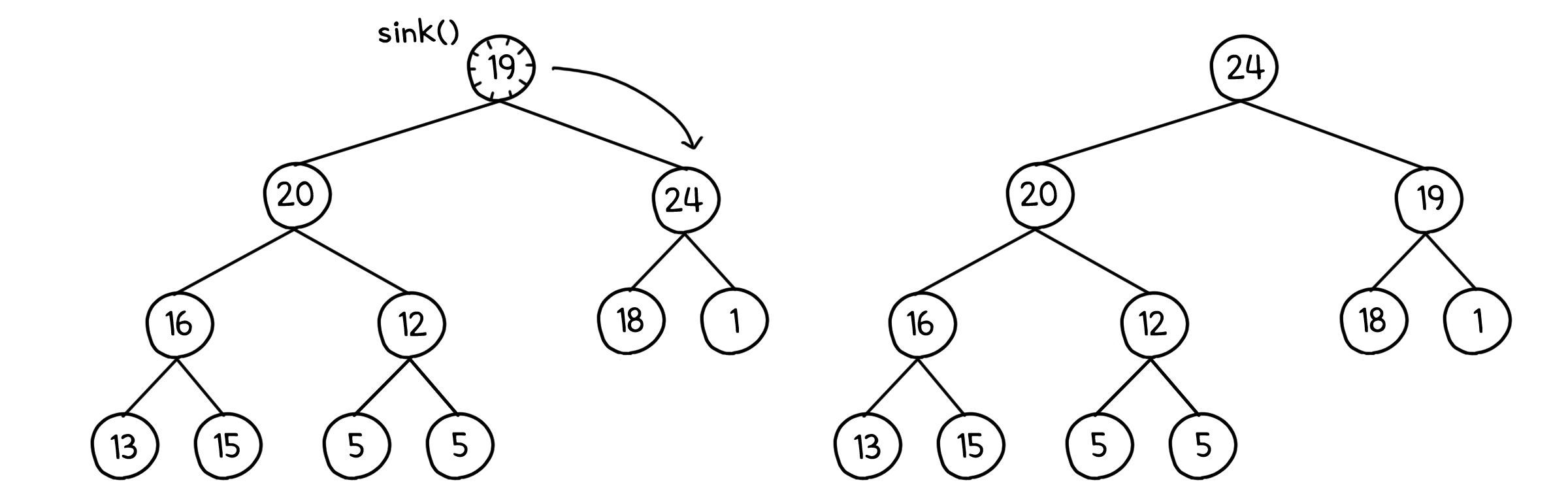
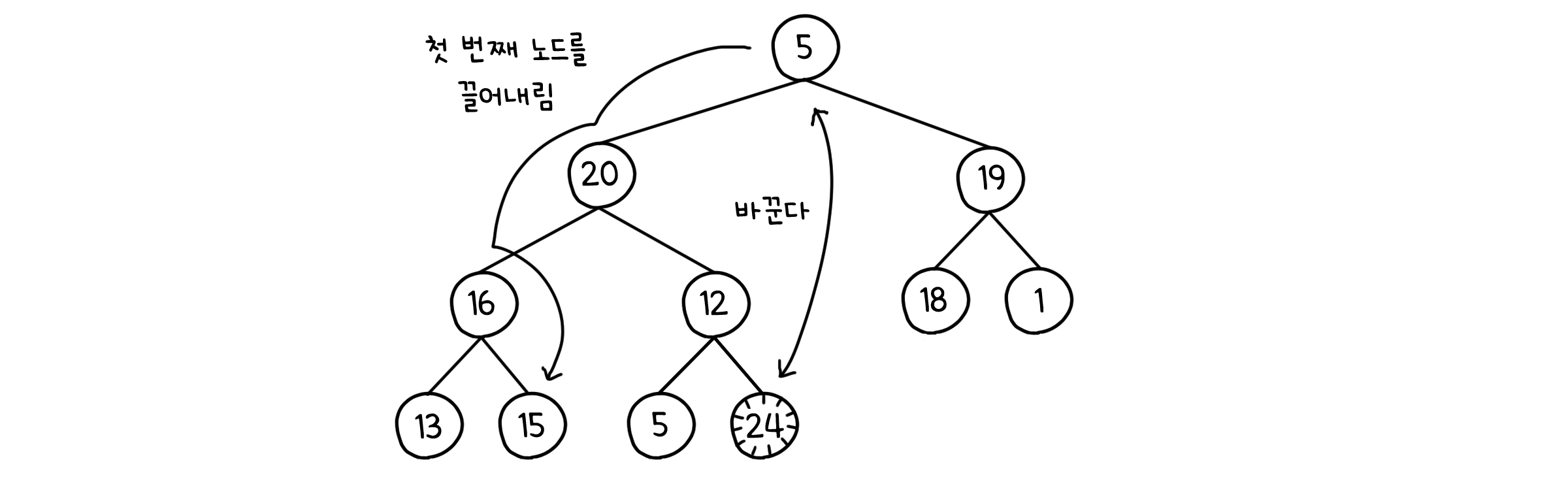
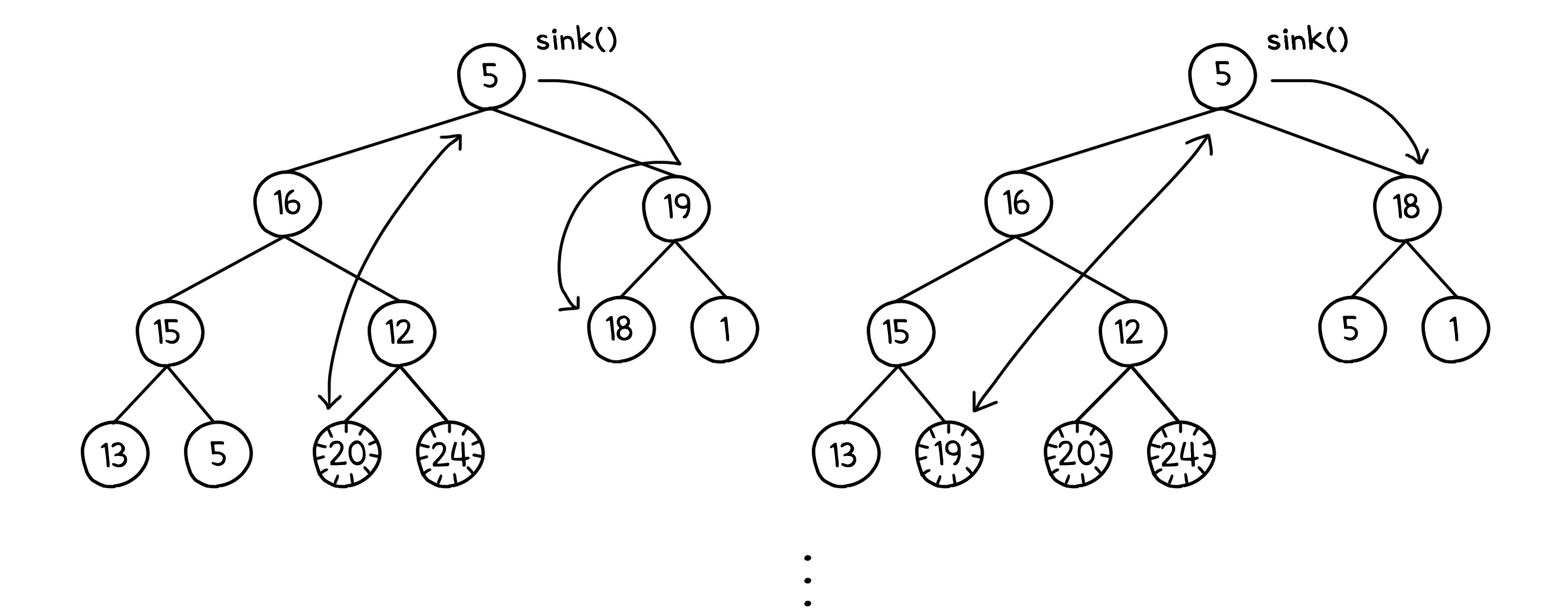
이제 이 배열은 힙이 되었습니다. 다음은 힙의 최댓값, 그러니까 루트 노드를 빼서 배열의 맨 뒤로 보내는 것을 반복하면 됩니다. 이 때 루트 노드를 힙의 맨 마지막 값과 바꾸게 되는데, 이러면 또 힙이 깨지기 때문에 sink( )를 통해 다시 복구를 해주어야 합니다.
그리고 뒤로 보내진 노드들은 이미 정렬이 된 노드들이기 때문에 힙의 범위에 포함하지 않아야 합니다. 루트 노드를 뺄 때마다 힙의 크기도 1씩 줄여서 해결할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
public void sort() {
for (int k = n/2; k >= 1; k--) { // 계산량을 줄이기 위해 잎 노드는 건너뜀
sink(k); // 밑에서부터 힙 복구
}
// 이 시점에서 힙 완성
while (n > 1) { // 힙을 모두 순회할 때까지
exch(1, n--); // 첫 번째 노드와 마지막 노드를 교환하고 힙 크기 한 칸 감소
sink(1); // 첫 번째 노드를 sink 시켜서 힙 복구
}
}
첫 번째 단계는 놀랍게도 $O(n)$의 시간으로 끝납니다. $O(logn)$ 시간의 sink( )가 n/2번 시행되는 것 같지만, 모든 노드가 같은 높이만큼 이동하지 않기 때문입니다. 하지만 두 번째 단계는 루트에서부터 sink( )를 n번 수행하기 때문에, 여지없이 $O(nlogn)$의 시간이 걸립니다.
또한 주목할 점은, 공간 사용이 없는 in-place 함수라는 것입니다. 재귀 호출이나 추가적인 배열을 사용하지 않았기 때문에 공간 복잡도는 $O(1)$이라고 할 수 있습니다. 여기서 다른 종류의 정렬 알고리즘과 비교해볼 수도 있긴 하지만, 아쉽게도 여기서 우리가 다루는 것은 데이터 구조에 대한 것이므로 나머지 이야기는 알고리즘 포스트에서 이어가도록 하겠습니다.
전체 코드 보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
public interface MaxPriorityQueue<K> {
int size();
boolean isEmpty();
K max();
void insert(K k);
K delMax();
}
public class MaxPQ<K extends Comparable<K>> implements MaxPriorityQueue<K> {
// member
private K[] pq;
private int n;
// constructor
public MaxPQ() { this(1); }
public MaxPQ(int CAPACITY) {
pq = (K[]) new Comparable[CAPACITY + 1];
n = 0
}
// methods
public int size() { return n }
public boolean isEmpty() { return size() == 0 }
public K max() { return pq[1] }
public void insert(K k) {
if(n == pq.length - 1) { resize(2 * pq.length); }
pq[++n] = k;
swim(n);
}
public K delMax() {
K max = pq[1];
exch(1, n--);
sink(1);
pq[n+1] = null;
if ((n > 0) && (n == (pq.length - 1) / 4)) { resize(pq.length / 2); }
return max;
}
public void sort() {
for (int k = n/2; k >= 1; k--)
sink(k);
while (n > 1) {
exch(1, n--);
sink(1);
}
}
// utility functions
private void resize(int n) {
K[] temp = (K[]) new Comparable[n];
for (int i = 1; i <= n; i++) { temp[i] = pq[i]; }
pq = temp;
}
private static boolean less(K v, K w) {
return v.compareTo(w) < 0
}
private static void exch(K[] a, int i, int j) {
K swap = a[i];
a[i] = a[j];
a[j] = swap;
}
private void swim(int k) {
while (k > 1 && less(k/2, k)) {
exch(k, k/2);
k = k/2;
}
}
private void sink(int k) {
while (2*k <= n) {
int j = 2*k;
if (j < n && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
}
![[CM202] 우선순위 큐와 힙 (Priority Queue & Heap)](/CMajor/assets/img/thumbnails/cm202/8.png)