[CM202] 07. 트리 (Tree)

 이제 우리는 순서대로 처리하는 선형적 구조를 가진 데이터 구조들을 거의 다 알아 보았습니다. 이제는 여러 계층을 가진 선형적이지 않은 구조에 대해서도 알아볼 차례입니다. 대표적인 비선형 구조인 트리에 대해 살펴봅시다.

트리는 그래프의 특수한 형태 중 하나로, 이산수학 분야에서 깊이 있게 다뤄지는 주제입니다. 트리에 대한 더 자세한 내용은 이산수학에서 다루며, 여기서는 구현을 위해 필수적으로 알아야 하는 개념만 소개하도록 하겠습니다.

트리 (Tree)

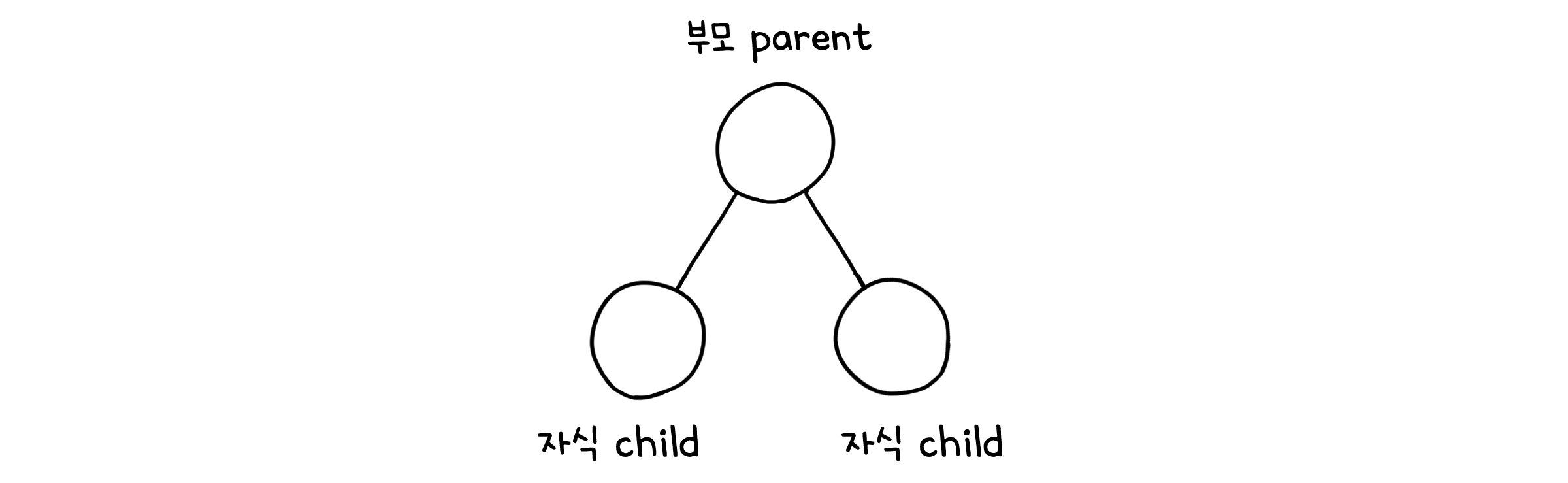
 트리(Tree)는 원소들이 부모(Parent)와 자식(Child) 관계로 연결된 계층적 구조의 ADT입니다. 즉, 리스트처럼 한 줄로 연결된 것이 아닌 한 노드가 여러 자식을 가질 수 있는 비선형 구조입니다. 현재 노드와 연결된 윗 계층의 노드를 부모, 아래 계층의 노드를 자식이라고 부릅니다. 만약 같은 노드의 자식들 사이에 특별한 순서가 존재한다면, 그 트리는 순서가 있다(Ordered tree)고 말할 수 있습니다.

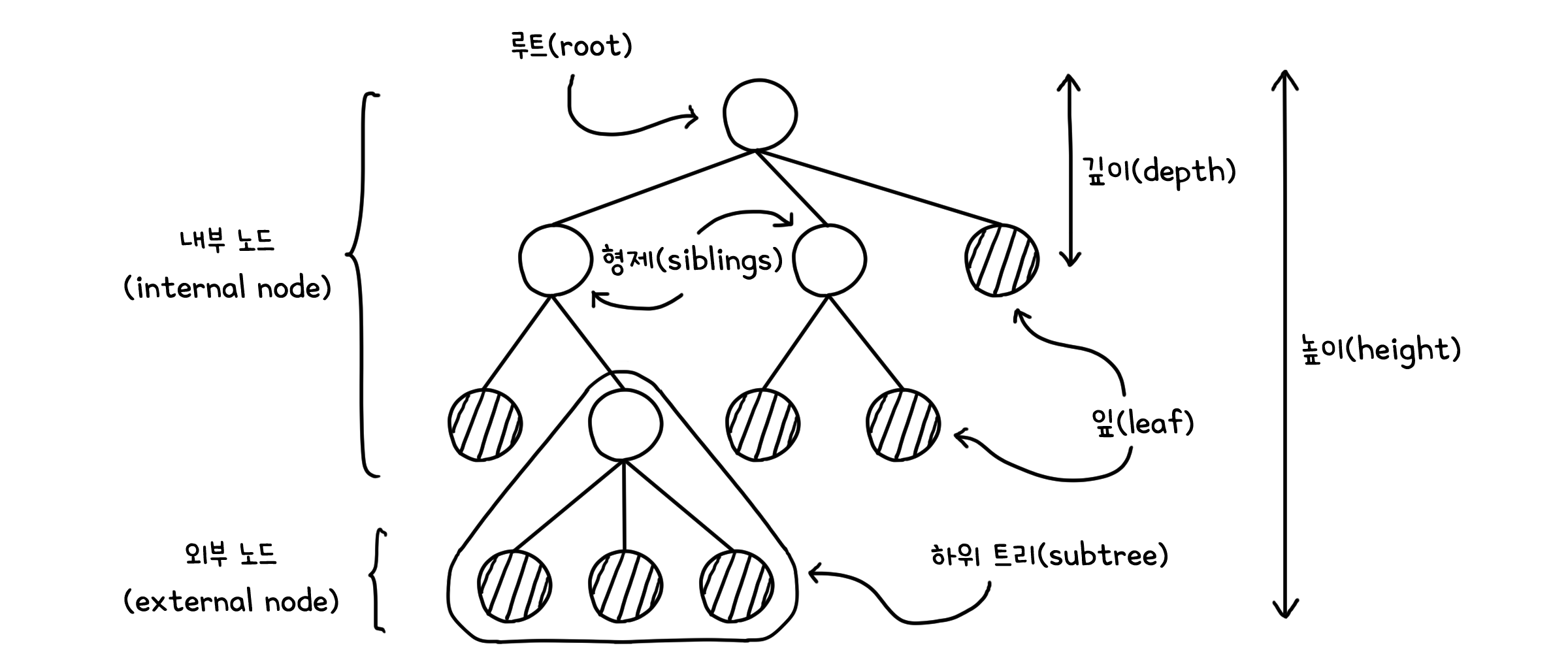
트리에 관한 몇 가지 용어들

이름	자료형
루트 (Root)	트리의 최상단 노드
형제 (Siblings)	같은 부모를 가지는 노드들
잎 (Leaf)	자식을 가지지 않는 노드
내부 노드 (Internal node)	최소 하나의 자식을 가진 노드
외부 노드 (External node)	자식이 없는 노드(=잎)
노드의 깊이 (Depth)	노드의 조상 수 (0부터 시작)
트리의 높이 (Height)	트리 안에서 노드 깊이의 최댓값 (0부터 시작)
하위 트리 (Subtree)	특정 노드를 루트로 하는 하위 트리

이진 트리 (Binary Tree)

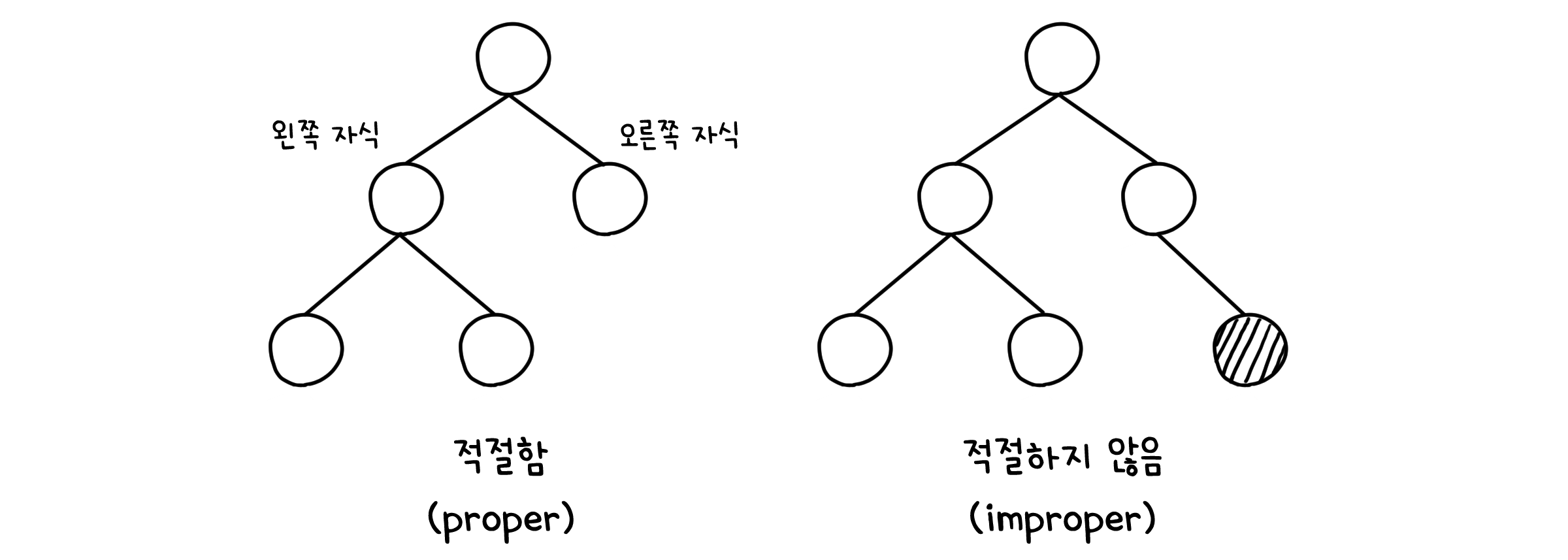
 트리 중에서도 자식을 두 개 까지만 가질 수 있는 조금 특수한 경우를 생각해봅시다. 그렇다면 두 자식을 오른쪽(Right child)과 왼쪽(Left child)으로 구분할 수 있을 것입니다. 모든 노드가 자식이 없거나 두 개 모두 가지고 있으면 적절하다(Proper)고 하고, 그렇지 않으면 적절하지 않다(Improper)고 합니다.

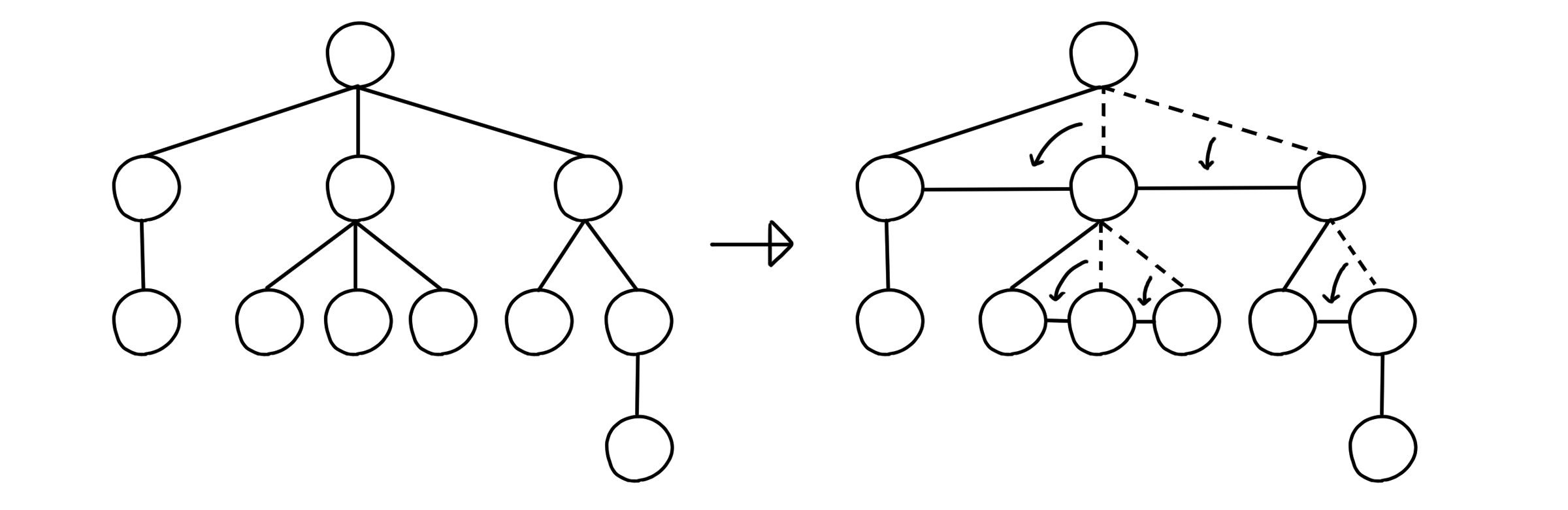
 일반적인 트리를 이진 트리로 변환할 때는 LCRS(Left-Child-Right-Sibling) 표기법을 사용하면 됩니다. 형제들 중에서 맨 왼쪽에 있는 자식은 그대로 두고, 나머지 자식들을 모두 부모 대신 자기 왼쪽에 있는 형제와 연결시켜버리는 방법이에요.

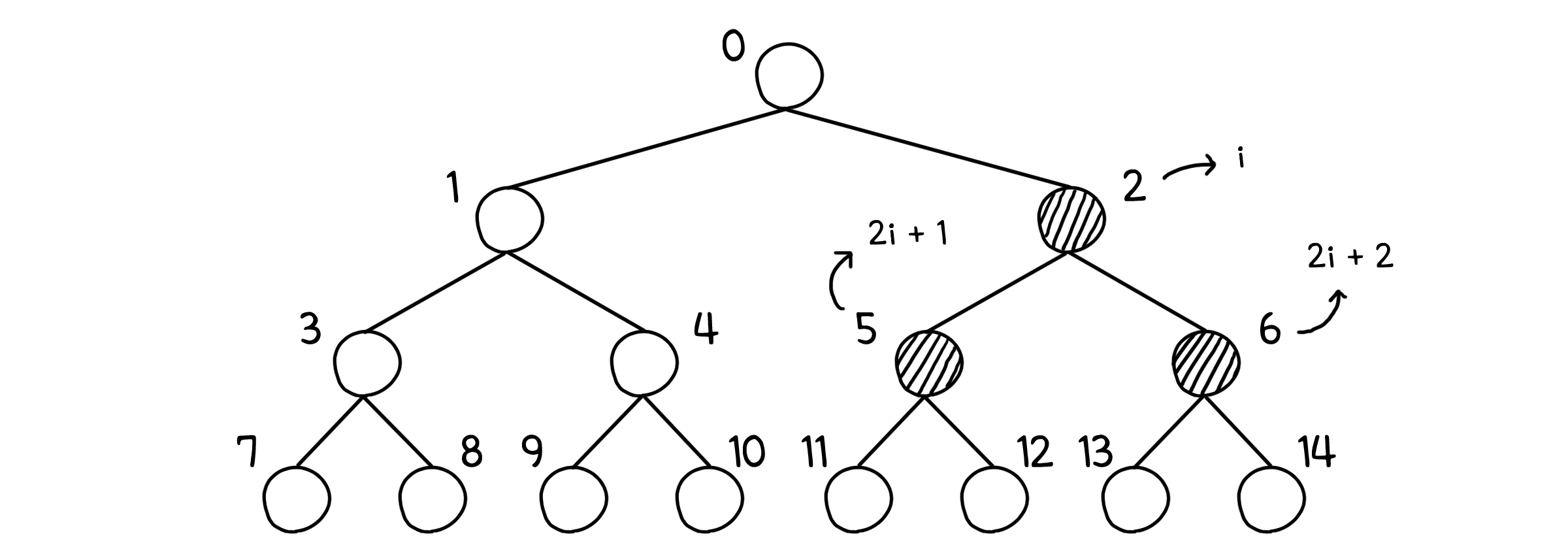
 트리에서 각 노드는 위에서 아래로, 왼쪽에서 오른쪽으로 순서가 매겨집니다. 만약 트리를 배열로 구현한다고 하면 이 순서 그대로 배열의 인덱스에 집어 넣으면 돼요. 이렇게 번호를 부여하면 $i$번째 노드의 자식은 몇 번째 노드가 되는지 쉽게 계산할 수 있습니다. 이진 트리의 경우 한 계층을 건너 갔으니 두 배, 그리고 왼쪽부터 오른쪽으로 순서가 매겨지니까 1, 2 만큼 더 하면 각각 $2i+1$, $2i+2$ 번째 노드가 되는 것이죠.

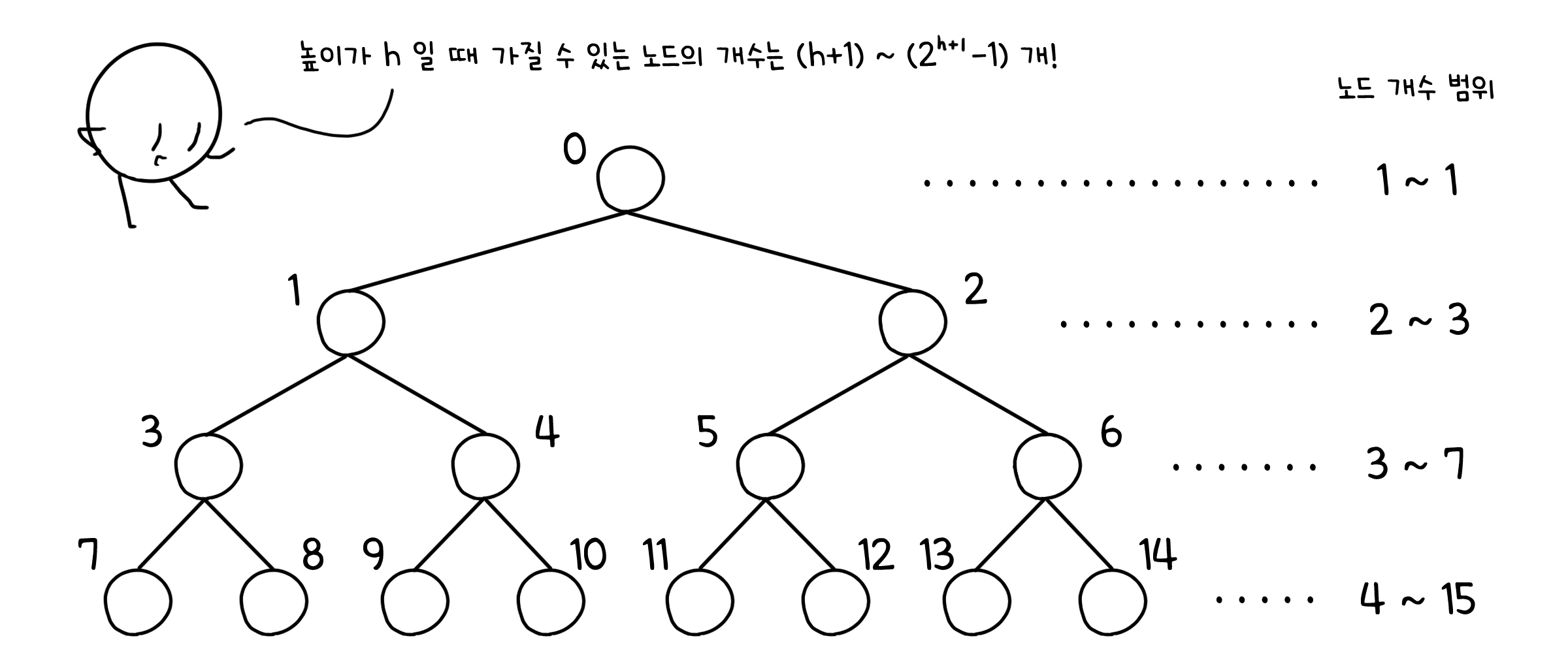
 또한 임의 높이 h의 트리가 최소, 혹은 최대 몇 개의 노드를 가질 수 있는지도 쉽게 알 수 있습니다.

이진 트리 순회하기

 이진 트리의 모든 노드들을 순회하는 방법에는 크게 세 가지가 있습니다.

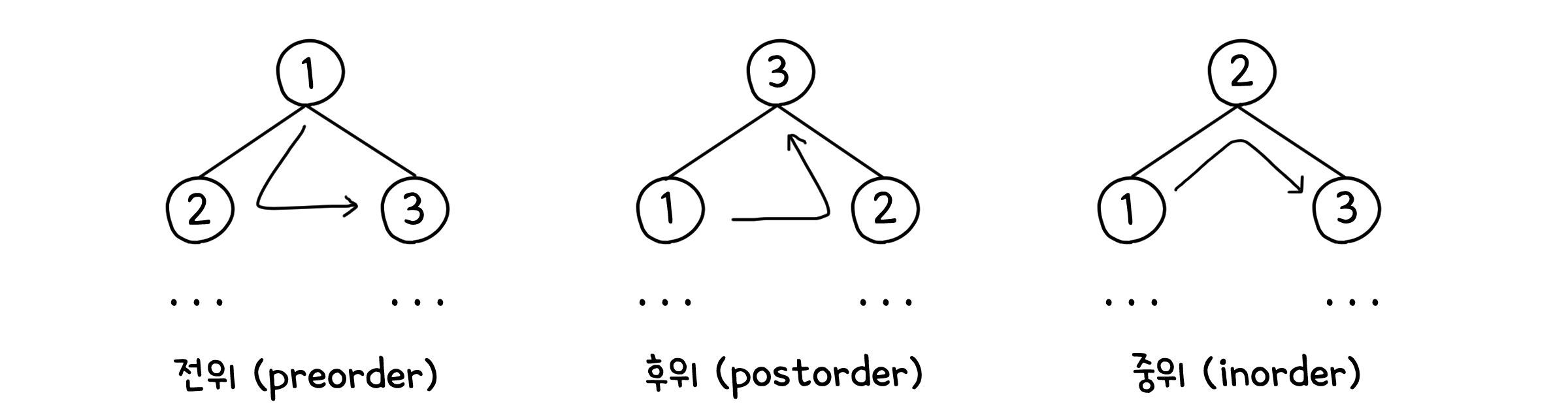
• 전위(Preorder) : 본 노드를 먼저 방문한 뒤 자식들을 방문하는 방법

• 후위(Postorder) : 자식들을 먼저 방문한 뒤 본 노드를 방문하는 방법

• 중위(Inorder) : 왼쪽 노드를 먼저 방문한 뒤 본 노드를 방문하고, 마지막으로 오른쪽 노드를 방문하는 방법

사실 이것 말고도 같은 계층의 노드들을 위에서 아래로 방문하는 너비 우선 탐색(Breath-First-Search) 방식도 있지만, 데이터 구조 보다는 알고리즘과 가까운 주제이기 때문에 더 자세히 다루지는 않겠습니다.

이진 탐색 트리 (Binary search tree)

 이진 트리를 소개한 이유는 노드를 탐색하는 속도가 빨라 데이터 접근/삽입/삭제에 유용한 구조이기 때문입니다. 탐색을 위해 구성한 특수한 조건의 이진 트리를 이진 탐색 트리(Binary search tree)라고 합니다.

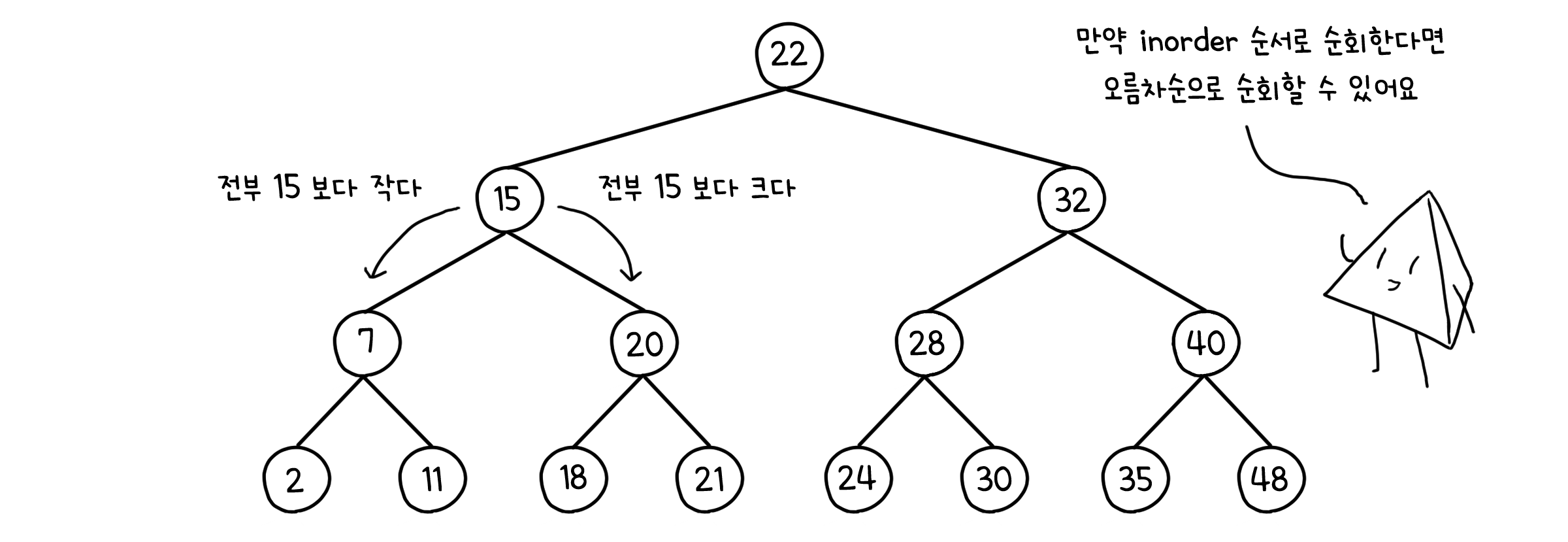
 이진 탐색 트리의 각 노드는 그 값의 대소관계에 따라 정렬되어 있습니다. 어떤 노드의 값을 $e$라고 했을 때, 그 노드의 왼쪽 하위 트리는 모두 $e$보다 작은 값을 가지고, 오른쪽 하위 트리는 모두 $e$보다 큰 값을 가지게 되는 식입니다.

 데이터 탐색에 어떻게 쓰이는지 알 것 같지 않나요? 노드마다 간단한 문답을 하면 됩니다. 내가 찾고자 하는 값이 현재 노드의 값보다 큰지 작은지를 물어보는 것이죠. 만약 작다면, 왼쪽 자식으로 내려가면 됩니다. 반대로 크다면, 오른쪽 자식으로 내려가겠죠. 둘 다 아니라면? 바로 거기가 우리가 찾는 곳이네요.

ADT: Tree

 트리 또한 다른 ADT와 마찬가지로 순회 가능하기 때문에 Iterable을 상속받습니다.

public interface Iterator<E>{
  boolean hasNext();  // 현재 요소에서 다음 요소가 있는지 반환
  E next();  // 현재 요소의 다음 요소를 반환
}

public interface Iterable<E> {
  Iterator<E> iterator();  // 반복자를 반환하는 메소드
}

public interface Tree<E> extends Iterable<E> {
  public int size();       // 트리의 크기 반환
  public boolean isEmpty();   // 비어 있는지 여부 반환
  public boolean search(E e); // 요소 탐색
  public void insert(E e);    // 요소 삽입
  public void delete(E e);    // 요소 제거
  public void inorder();      // 중위 순회
  public void postorder();    // 후위 순회
  public void preorder();     // 전위 순회
}

데이터 구조: BST

 Tree의 ADT 구조를 가지면서 이진 탐색 트리를 구현해봅시다. 이 때 중요한 것은, 이 데이터 구조가 가지는 값들은 반드시 서로 비교가 가능해야 한다는 것입니다. 그래야 각 노드들을 적절히 배치할 수 있으니까요. 그렇기 때문에 BST가 가지는 값의 자료형 E는 비교 가능하다는 조건을 명시해야 합니다.

// java에서 Comparable<E>은 java.lang.Comparable 에 미리 구현되어 있습니다.

public interface Comparable<E> {
  int compareTo(E other);  // (자기자신 - other)의 결과값을 반환.
  // 결과값 < 0 : 자기자신 < other
  // 결과값 = 0 : 자기자신 < other
  // 결과값 > 0 : 자기자신 > other
}

                 // E는 비교 가능해야 함 //
public class BST<E extends Comparable<E>> implements Tree<E> {
  // ...
}

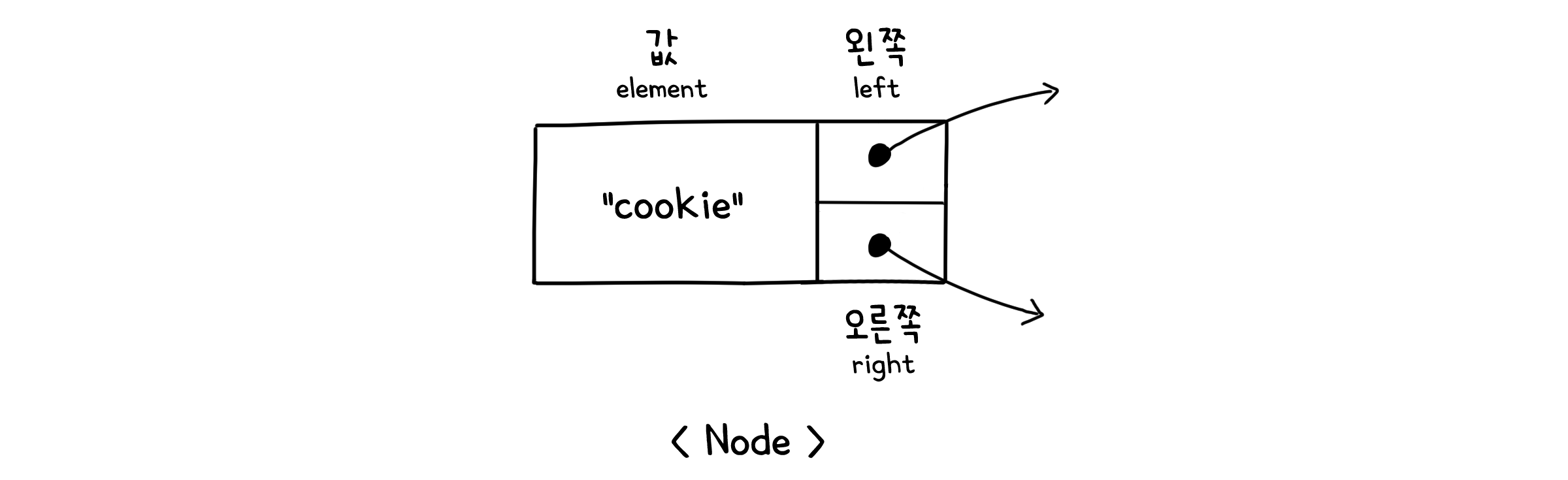
 또한 기존의 Node 클래스를 새로 정의해야 할 필요가 있습니다. 이전까지의 Node는 연결되는 노드가 하나 뿐이었지만, 이진 트리에서는 두 개의 노드와 연결되니까요. 우리는 next 대신 left와 right 두 개의 값을 사용해야 합니다.

Node - 멤버

이름	자료형	기본값	기능
element	E	-	값
left	Node<E>	-	왼쪽 자식
right	Node<E>	-	오른쪽 자식

BST - 멤버

 트리 구조는 루트 노드를 맨 첫 번째 요소로 합니다. 물론 처음엔 비어 있는 상태이기 때문에 아무 값도 가지지 않습니다.

이름	자료형	기본값	기능
root	Node<E>	-	루트 노드
size	int	0	크기

BST - 메소드

 Tree의 메소드 말고도 루트 노드를 가져오는 getRoot( ) 메소드를 추가하였습니다.

이름	매개변수	반환값	기능
size()	-	int	트리의 크기 반환
isEmpty()	-	boolean	비어 있는지 여부 반환
search(E e)	e : 요소	boolean	요소 탐색
insert(E e)	e : 요소	-	요소 삽입
delete(E e)	e : 요소	-	요소 제거
inorder()	-	-	중위 순회
postorder()	-	-	후위 순회
preorder()	-	-	전위 순회
getRoot()	-	Node<E>	루트 노드 반환

메소드 살펴보기

search( )

public boolean search(E e) {
  Node<E> x = root;  // 루트에서 부터 시작

  while (x != null) {  // 트리 끝으로 갈 때까지
    int cmp = e.compareTo((E) x.element);  // 현재 노드 값과 비교
    if      (cmp < 0) { x = x.left; }  // 작다면 왼쪽 자식으로
    else if (cmp > 0) { x = x.right; }  // 크다면 오른쪽 자식으로
    else    return true;  // 같다면 찾았으니 참 반환
  }
  
  return false;  // 끝날 때 까지 못 찾았으면 거짓 반환
}

insert( )

 insert( )를 비롯한 대부분의 메소드들은 재귀를 사용합니다. 그래서 메소드 안에 또 다른 재귀 함수를 정의해 이를 호출하는 방식을 사용하였습니다.

public void insert(E e) {
  private Node<E> insert(Node<E> x, E e){
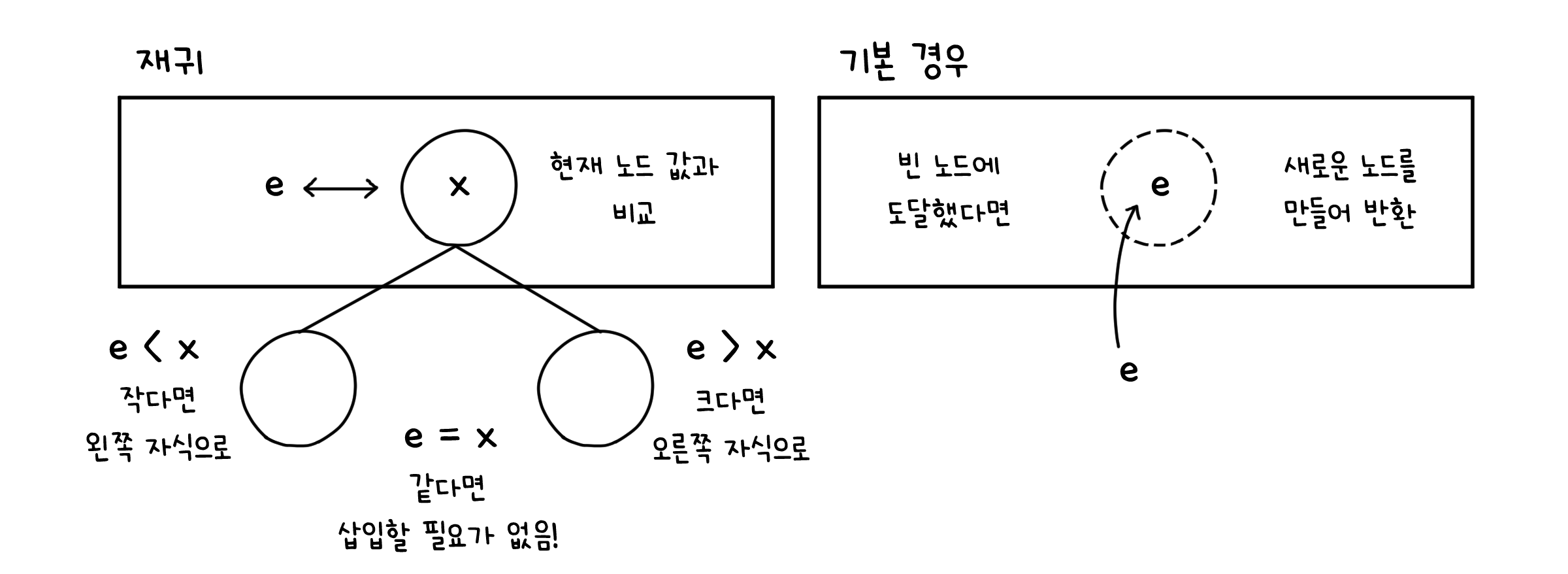
    if (x == null) {  // 빈 노드(=트리의 끝)에 도달했다면
      size++;  // 크기 한 칸 증가
      return new Node(e);  // 새로운 노드를 만들어 반환
    }

    int cmp = e.compareTo((E) x.element);  // 현재 노드 값과 비교
    if      (cmp < 0) { x.left = insert(x.left, e); }  // 작다면 왼쪽 자식으로
    else if (cmp > 0) { x.right = insert(x.right, e); }  // 크다면 오른쪽 자식으로
    else              { x.element = e; }  // 같다면 삽입할 필요가 없음

    return x;
  }

  root = insert(root, e);
}

delete( )

 delete( )는 조금 복잡합니다. insert( )는 무조건 노드가 맨 끝에 추가되는 방식이었지만, delete( )는 내부 노드에서도 발생할 수 있으니까요. 이 경우 하위 트리가 위로 올라와 재정렬되어야 하기 때문에 몇 가지 보조 함수들을 더 만들어 해결해야 합니다.

// min(Node<E> x) : x를 루트로 하는 트리에서 최솟값을 찾아 반환합니다.
private Node<E> min(Node<E> x) {
  if (x.left == null) return x  // 왼쪽 자식이 없다면 본인이 제일 작은 값
  else return min(x.left)  // 왼쪽 하위 트리에서 최솟값 탐색
}

// deleteMin(Node<E> x) : x를 루트로 하는 트리에서 최솟값을 찾아 제거합니다.
private Node<E> deleteMin(Node<E> x) {
  if (x.left == null) {  // 왼쪽 자식이 없다면
    size--;  // 크기 한 칸 감소
    return x.right  // 오른쪽 자식이 현재 노드의 위치로
  }
  x.left = deleteMin(x.left);  // 왼쪽 자식에서 최솟값을 없앤 후 결과
  return x;  // 현재 노드는 그대로
}

// delete(E e) : 본 함수
public void delete(E e) {
  private Node<E> delete(Node<E> x, E e) {
    if (x == null) {  // 빈 노드(=트리의 끝)에 도달했다면
      return null;  // 아무것도 반환하지 않음
    }

    int cmp = e.compareTo((E) x.element);  // 현재 노드 값과 비교
    if      (cmp < 0) { x.left = delete(x.left, e); }  // 작다면 왼쪽 자식으로
    else if (cmp > 0) { x.right = delete(x.right, e); }  // 크다면 오른쪽 자식으로
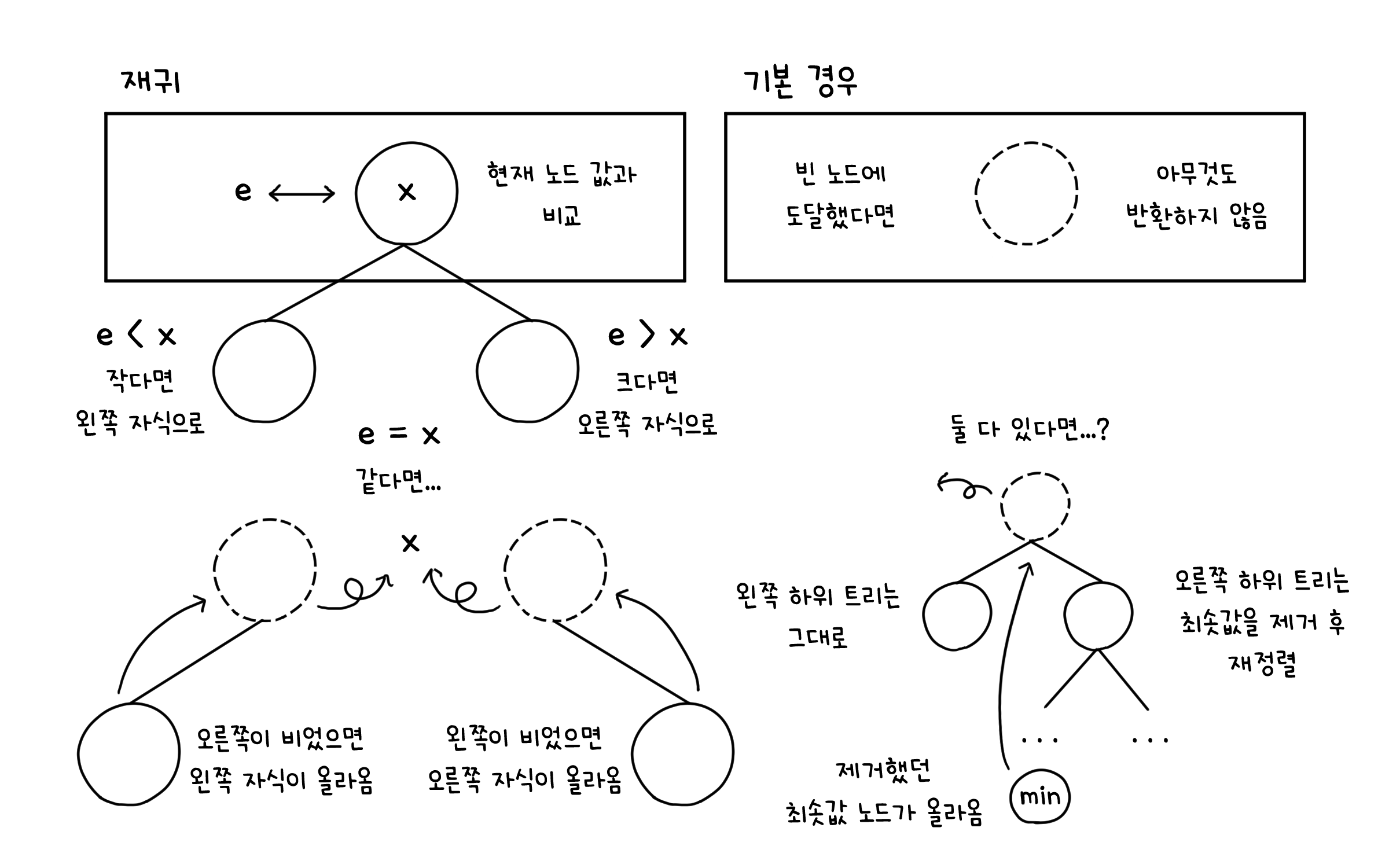
    else              {  // 같다면...
      if (x.right == null) {  // 오른쪽이 비었으면
        return x.left;  // 왼쪽 자식이 현재 노드 자리로 올라옴
      }
      if (x.left == null) {  // 왼쪽이 비었으면
        return x.right;  // 오른쪽 자식이 현재 노드 자리로 올라옴
      }
      
      // 두 자식 모두 존재한다면...
      Node<E> t = x;  // 현재 노드 저장
      x = min(t.right);  // 현재 노드의 오른쪽 자식 내에서 최솟값을 가진 노드
      x.right = deleteMin(t.right);  // 그 노드가 빠진 후 정렬된 하위 트리를 오른쪽에
      x.left = t.left;  // 왼쪽 하위 트리는 그대로

      size--;  // 크기 한 칸 감소
      return x;  // 구했던 최솟값 노드를 현재 노드 자리로
    }
  }

  root = delete(root, e);
}

inorder( )

public void inorder() {
  private void inorder(Node<E> x){
    if (x == null) { return }  // 빈 노드(=트리의 끝)에 도달했다면 다시 돌아감

    inorder(x.left);  // 1. 왼쪽
    System.out.print(x.element + " ");  // 2. 본인
    inorder(x.right);  // 3. 오른쪽
  }

  inorder(root);
}

postorder( )

public void postorder() {
  private void postorder(Node<E> x){
    if (x == null) { return }  // 빈 노드(=트리의 끝)에 도달했다면 다시 돌아감

    postorder(x.left);  // 1. 왼쪽
    postorder(x.right);  // 2. 오른쪽
    System.out.print(x.element + " ");  // 3. 본인
  }

  postorder(root);
}

preorder( )

public void preorder() {
  private void preorder(Node<E> x){
    if (x == null) { return }  // 빈 노드(=트리의 끝)에 도달했다면 다시 돌아감

    System.out.print(x.element + " ");  // 1. 본인
    preorder(x.left);  // 2. 왼쪽
    preorder(x.right);  // 3. 오른쪽
  }

  preorder(root);
}

 이진 탐색 트리는 왼쪽, 중간, 오른쪽 순서로 대소 관계를 지키기 때문에 효율적인 탐색과 탐색을 이용한 삽입/삭제를 가능하게 해 줍니다. 하지만 역시 문제점도 존재하는데, 만약 트리의 한 쪽에만 노드가 몰리면 불균형한 모양이 만들어질 수 있다는 것입니다. 각 노드의 깊이가 고르지 못하면, 운이 안 좋을 때 탐색하기 위해 들어가야 하는 깊이가 깊어질 수 있습니다. 물론 이를 해결한 좀 더 좋은 성능의 트리 구조도 존재합니다. 하지만 그건 나중에 좀 더 알아보도록 하죠.

전체 코드 보기

// interface: Iterator
public Interface Iterator<E> {
  boolean hasNext();
  E next();
}
// interface: Iterable
public interface Iterable<E> {
  Iterator<E> iterator();
}
// interface: Tree
public interface Tree<E> extends Iterable<E> {
  int size();
  boolean isEmpty();
  boolean search(E e);
  void insert(E e);
  void delete(E e);
  void inorder();
  void postorder();
  void preorder();
}

public class BST<E extends Comparable<E>> implements Tree<E> {
  // nested class: Node
  private static class Node<E> {
    // member
    E element;
    Node<E> left;
    Node<E> right;

    // constructor
    public Node(E e) {
      element = e;
    }
  }

  // member
  private Node<E> root;
  private int size;
  
  // constructor
  public BST() { }
  public BST(E[] objects) {
    for (int i = 0; i < objects.length; i++) {
      insert(objects[i]);
    }
    size = 0;
  }

  // methods
  public int size() { return size }

  public boolean isEmpty() { return size() == 0 }

  public boolean search(E e) {
    Node<E> x = root;

    while (x != null) {
      int cmp = e.compareTo((E) x.element);

      if      (cmp < 0) { x = x.left; }
      else if (cmp > 0) { x = x.right; }
      else    return true;
    }
    
    return false;
  }

  public void insert(E e) {
    private Node<E> insert(Node<E> x, E e){
      if (x == null) {
        size++;
        return new Node(e);
      }

      int cmp = e.compareTo((E) x.element);
      if      (cmp < 0) { x.left = insert(x.left, e); }
      else if (cmp > 0) { x.right = insert(x.right, e); }
      else              { x.element = e; }

      return x;
    }

    root = insert(root, e);
  }

  public void delete(E e) {
    private Node<E> delete(Node<E> x, E e) {
      if (x == null) { return null; }

      int cmp = e.compareTo((E) x.element);
      if      (cmp < 0) { x.left = delete(x.left, e); }
      else if (cmp > 0) { x.right = delete(x.right, e); }
      else              {
        if(x.right == null) return x.left;
        if(x.left == null) return x.right;

        Node<E> t = x;
        x = min(t.right);
        x.right = deleteMin(t.right);
        x.left = t.left;

        size--;
        return x; 
      }
    }

    root = delete(root, e);
  }

  public void inorder() {
    private void inorder(Node<E> x){
      if (x == null) { return }
      inorder(x.left);
      System.out.print(x.element + " ");
      inorder(x.right);
    }

    inorder(root);
  }

  public void postorder() {
    private void postorder(Node<E> x){
      if (x == null) { return }
      postorder(x.left);
      postorder(x.right);
      System.out.print(x.element + " ");
    }

    postorder(root);
  }

  public void preorder() {
    private void preorder(Node<E> x){
      if (x == null) { return }
      System.out.print(x.element + " ");
      preorder(x.left);
      preorder(x.right);
    }

    preorder(root);
  }

  public Node<E> getRoot() { return root }

  // utility functions
  public E min() {
    private Node<E> min(Node<E> x) {
      if (x.left == null) return x
      return min(x.left)
    }

    if (isEmpty()) return null
    return min(root).element
  }

  public void deleteMin() {
    private Node deleteMin(Node x) {
      if (x.left == null) {
        size--;
        return x.right
      }
      x.left = deleteMin(x.left);
      return x
    }

    root = deleteMin(root);
  }
}