[CM202] 05. 스택 & 큐 (Stack & Queue)

게시 2025/10/30 업데이트 2025/11/08

16 분정도 걸립니다

[CM202] 05. 스택 & 큐 (Stack & Queue)

앞서 우리는 두 가지 기본적인 데이터 구조에 대해 살펴 보았습니다. 이제는 이 데이터 구조들을 사용해 구현할 수 있는 자료형, 그러니까 ADT에 대해서도 본격적으로 알아봐야 할 때가 되었습니다. 첫 번째로, 가장 많이 쓰이는 ADT인 스택과 큐에 대해 소개합니다.

스택 & 큐 (Stack & Queue)

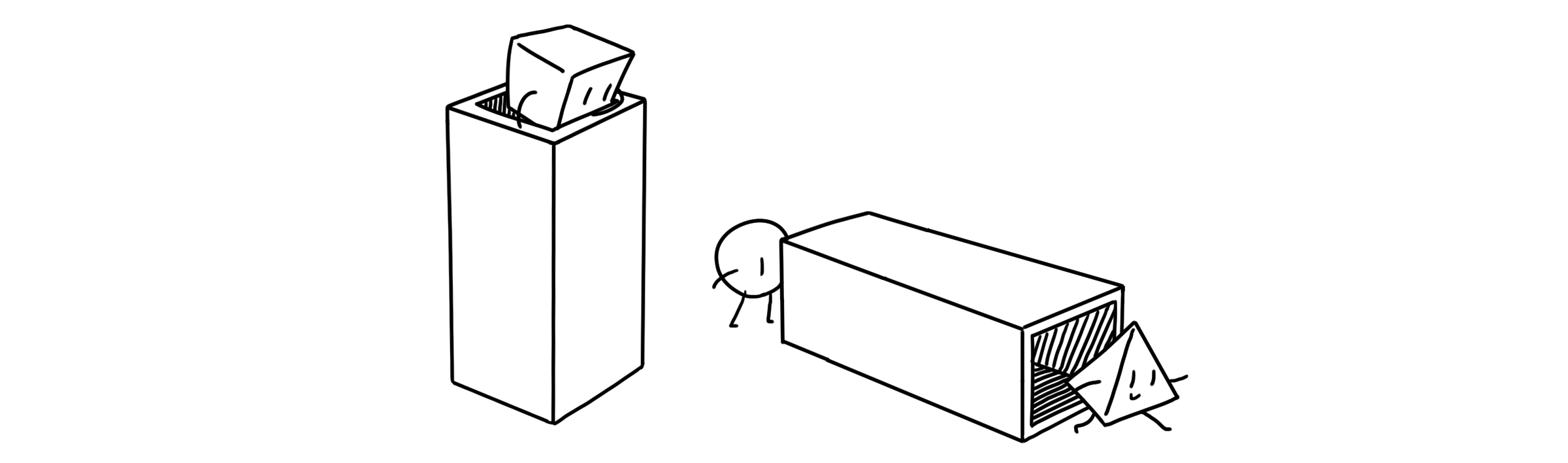
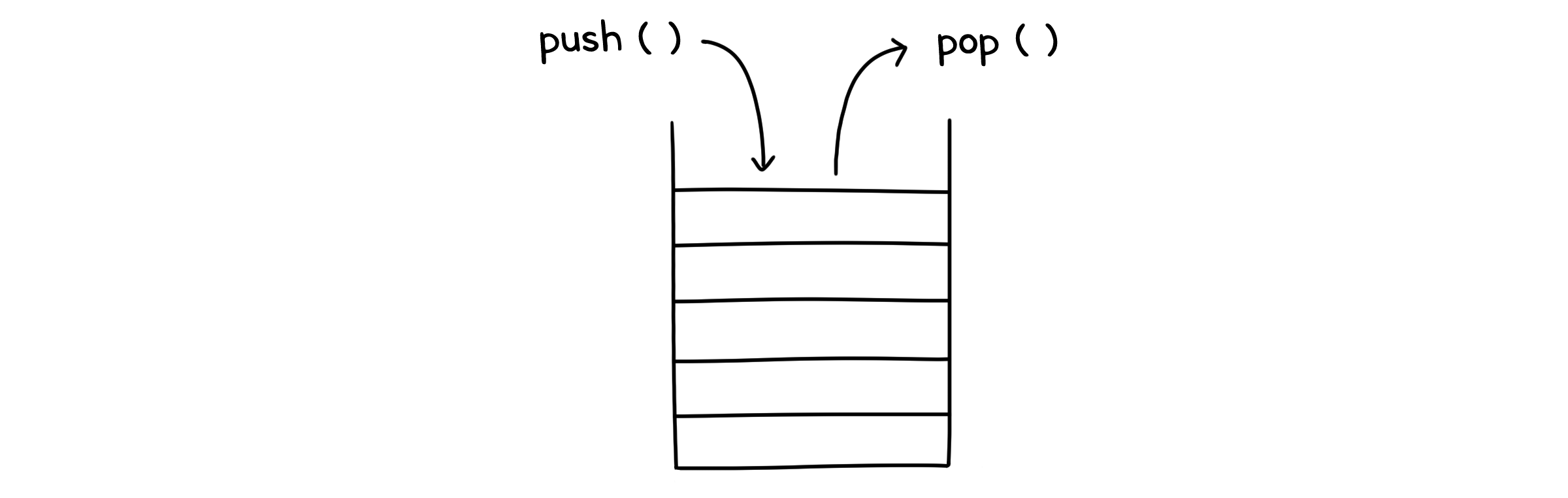
스택(Stack)은 가장 나중에 들어간 요소가 제일 먼저 나가게 되는 LIFO(Last-In-First-Out) 구조의 ADT입니다. 보통 가방에 짐을 쌀 때 제일 먼저 챙기는 물건이 제일 아래에 들어가게 되고, 짐을 풀 때 마지막으로 꺼내게 되죠. 같은 순서라고 생각하면 됩니다. 스택에서 값을 넣을 때는 안으로 밀어 넣기 때문에 push라는 이름으로 부르고, 반대로 값을 뺄 때는 pop이라고 부릅니다.

큐(Queue)는 제일 먼저 들어간 요소가 제일 먼저 나가게 되는 FIFO(First-In-First-Out) 구조의 ADT입니다. 네, 선입선출이에요. 그 외에도 대기 줄을 서는 구조 또한 먼저 기다린 사람이 먼저 나가니 큐라고 생각할 수 있습니다. 큐는 값을 넣고 빼는 것을 조금 형식적인 이름으로 부릅니다. 값을 넣을 때는 enqueue, 뺄 때는 dequeue라고 합니다.

참고로, 스택과 큐는 모두 크기의 제한이 없습니다.

ADT: Stack

2장에서 언급했듯, ADT는 데이터 구조와 달리 자료형을 추상적으로 묘사하는 상태입니다. 구현 코드 없이 자료형에 필요한 조건만을 나열해도 충분하다는 것이죠. 이런 방식 처럼 특정 객체에 포함된 기능이나 값들에 대해 서술한 것을 API(Applications Programming Interface)라고 합니다. API를 통해 정의된 ADT는 서로 다른 데이터 구조들을 사용하여 다양한 방식으로 구현할 수 있습니다.

이제 스택의 ADT에 대해 정의해보겠습니다.

  
public interface Stack<E> {
  int size();         // 스택의 크기 반환
  boolean isEmpty();  // 비어 있는지 여부 반환
  void push(E e);     // 요소 추가
  E pop();            // 요소 제거
  E top();            // 맨 위의 요소 반환
}

위의 구문은 Java의 interface 구문입니다. interface는 클래스를 정의할 때 어떤 요소가 필수적으로 있어야 하는지 안내해주는 가이드라인 역할을 합니다. 자세한 문법은 몰라도 지장이 없으며, 어떤 값이나 함수가 선언되어 있는지만 확인해도 충분합니다.

데이터 구조: ArrayStack

스택을 구현해볼 첫 번째 데이터 구조는 역시 배열입니다. 배열은 크기가 정해져 있어야 하기 때문에, 객체를 만들 때 부터 최대 용량(=CAPACITY)을 정해 놓아야 합니다.

ArrayStack - 멤버

이름	자료형	기본값	기능
data	E[]	-	배열
n	int	-1	크기
CAPACITY	int	1000	전체 용량

ArrayStack - 메소드

이름	매개변수	반환값	기능
size()	-	int	길이 반환
isEmpty()	-	boolean	비어 있는지 여부
push(E e)	-	-	요소 추가
pop()	-	E	요소 제거
top()	-	E	맨 위 요소 반환

메소드 살펴보기

push( )

  
public void push(E e) {
  data[++n] = e;  // 크기를 한 칸 늘리고 요소 추가
}

pop( )

  
public E pop() {
  if (isEmpty()) {  // 스택이 비었다면
    return null;  // 아무것도 반환하지 않음
  }

  E answer = data[n];  // 맨 위의 요소 선택
  data[n] = null;  // 그 자리는 비움
  n--;  // 크기 한 칸 감소

  return answer;
}

배열이 고정된 크기를 가진다는 말은, 곧 스택이 계속 쌓이다 배열의 크기를 넘으면 더 이상 값을 넣을 수 없다는 뜻입니다. 이 경우 프로그램은 FullStackException 등과 같은 예외를 던져 에러를 발생시킵니다. 값을 무한정 넣고 싶은 사용자 입장에서 썩 유쾌한 특징은 아니죠.

데이터 구조: LinkedStack

고정된 크기가 문제라면 연결 리스트 구조를 이용하면 문제를 해결할 수 있을지도 모릅니다. 연결 리스트를 사용하는 가장 간단한 방법은, 이전 장에서 만들었던 데이터 구조인 SinglyLinkedList를 바로 사용하는 것입니다.

LinkedStack - 멤버

이름	자료형	기본값	기능
list	SinglyLinkedList	empty	연결 리스트

LinkedStack - 메소드

이름	매개변수	반환값	기능
size()	-	int	길이 반환
isEmpty()	-	boolean	비어 있는지 여부
push(E e)	-	-	요소 추가
pop()	-	E	요소 제거
top()	-	E	맨 위 요소 반환

메소드 살펴보기

SinglyLinkedList 객체를 사용하면 스택을 굉장히 간단하게 구현할 수 있습니다. 리스트의 앞과 뒤에 요소를 추가하거나 제거하는 메소드들이 SinglyLinkedList 객체에 이미 구현되어 있으니까요. 그저 적절할 함수를 선택해 호출하면 될 뿐입니다.

push( )

  
public void push(E e) {
  list.addFirst(E e);  // 맨 위에 추가
}

pop( )

  
public E pop() {
  list.removeFirst();  // 맨 위 요소 제거
}

데이터 구조: StackNode

그래도 이대로 넘어가기엔 싱거우니까, 연결 리스트와 노드를 직접 사용해 스택을 구현해 봅시다. 노드 객체는 이전 장에서 정의한 클래스를 그대로 사용하겠습니다.

  
private static class Node<E> {
  private E item;
  private Node<E> next;
}

StackNode - 멤버

이름	자료형	기본값	기능
first	Node<E>	null	맨 위의 요소
n	int	0	크기

StackNode - 메소드

이름	매개변수	반환값	기능
size()	-	int	길이 반환
isEmpty()	-	boolean	비어 있는지 여부
push(E e)	-	-	요소 추가
pop()	-	E	요소 제거
top()	-	E	맨 위 요소 반환

메소드 살펴보기

push( )

  
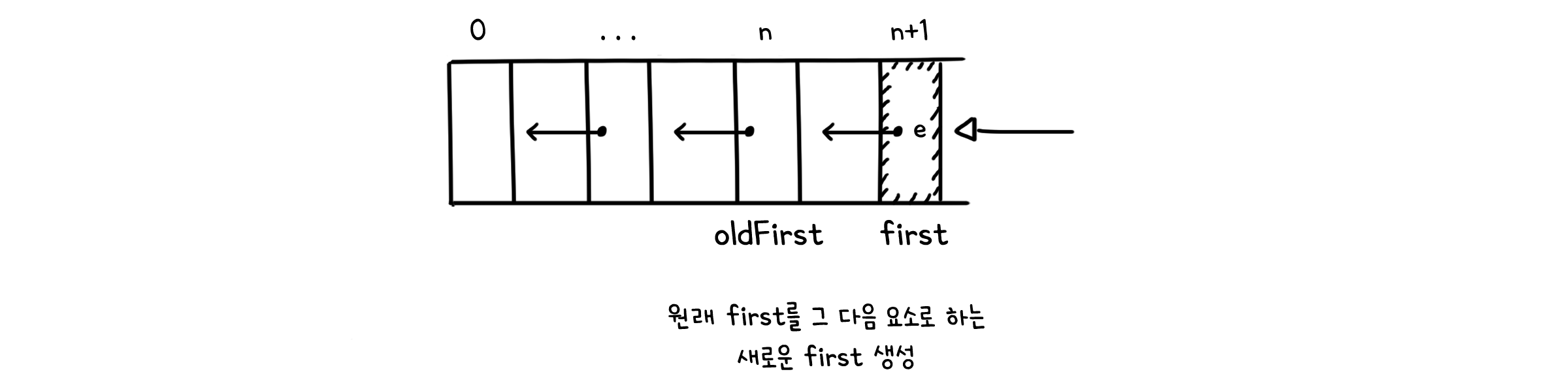
public void push(E e) {
  Node<E> oldfirst = first;  // first 요소 저장
  first = new Node<E>(e, oldfirst);  // 원래 first를 그 다음 요소로 하는 새로운 first 생성
  n++;  // 크기 한 칸 증가
}

pop( )

  
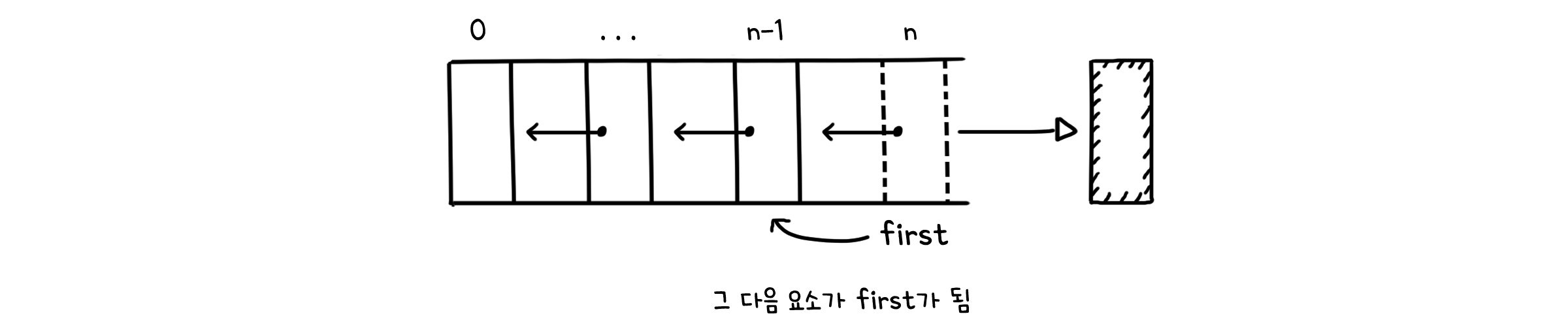
public E pop() {
  E item = first.item;  // 맨 위 값 가져오기
  first = first.next;  // 그 다음 요소가 first가 됨
  n--;  // 크기 한 칸 감소

  return item;
}

ADT: Queue

이번에는 큐를 구현해봅시다. 마찬가지로 ADT 정의를 먼저 해야겠죠.

  
public interface Queue<E> {
  int size();         // 스택의 크기 반환
  boolean isEmpty();  // 비어 있는지 여부 반환
  void enqueue(E e);  // 요소 추가
  E dequeue();        // 요소 제거
  E first();          // 맨 위의 요소 반환
}

데이터 구조: QueueNode

배열의 한계점을 알았으니, 이번에는 바로 연결 리스트를 사용해 큐를 구현해봅시다. 마찬가지로 SinglyLinkedList를 사용할 수 있지만, 구현방법은 간단하니 넘어가도록 하겠습니다.

QueueNode - 멤버

이름	자료형	기본값	기능
first	Node<E>	null	맨 앞의 요소
last	Node<E>	null	맨 뒤의 요소
n	int	0	크기

QueueNode - 메소드

이름	매개변수	반환값	기능
size()	-	int	길이 반환
isEmpty()	-	boolean	비어 있는지 여부
enqueue(E e)	-	-	요소 추가
dequeue()	-	E	요소 제거
top()	-	E	맨 위 요소 반환

메소드 살펴보기

enqueue( )

  
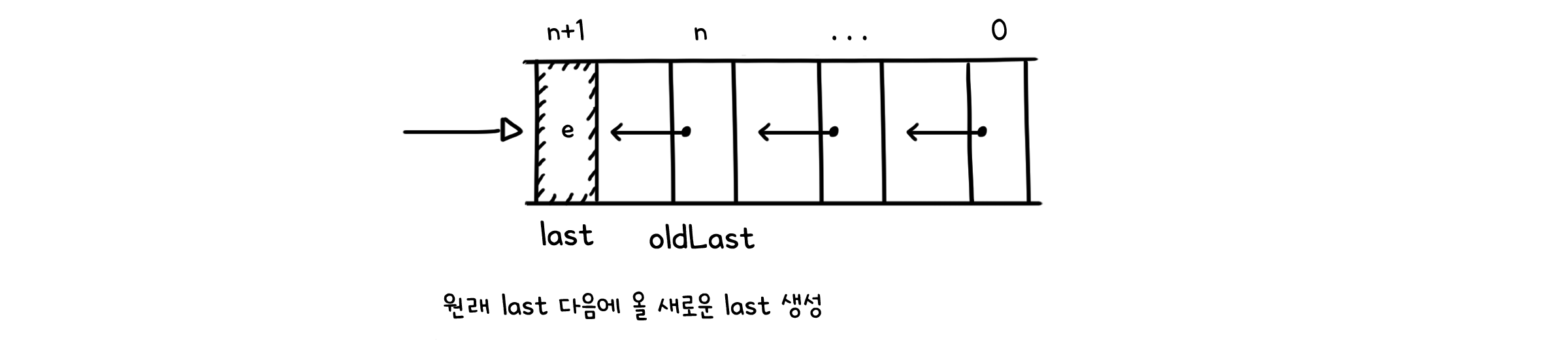
public void enqueue(E e) {
  Node<E> oldlast = last;  // last 요소 저장
  last = new Node<E>(e, null);  // 원래 last 다음에 올 새로운 last 생성

  if (isEmpty()) {  // 큐가 비어 있었다면
    first = last;  // last 이전에 올 값은 없으므로 last가 first
  }
  else {  // 이전 값이 있으면
    oldlast.next = last;  // 원래 last의 다음 값이 새로운 last
  }
  n++;  // 크기 한 칸 증가
}

dequeue( )

  
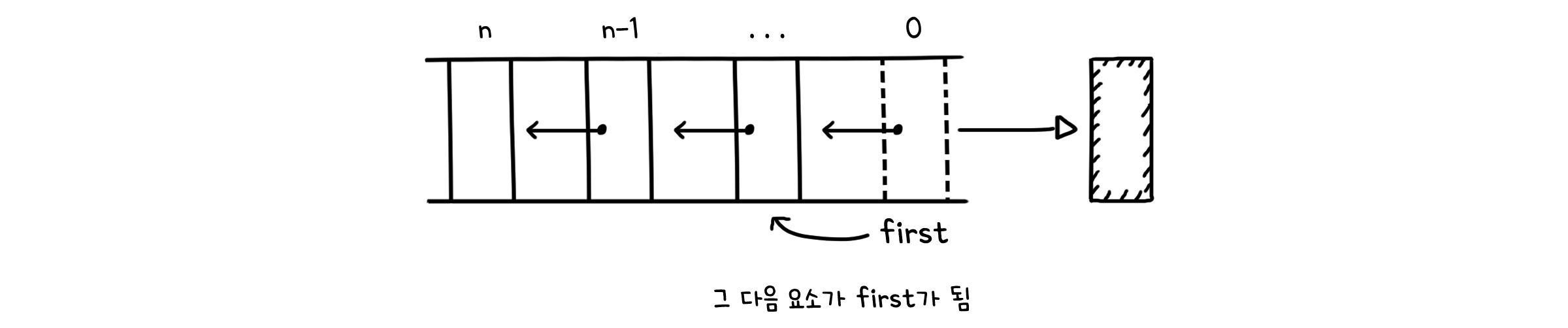
public void dequeue(E e) {
  if (isEmpty()) {  // 큐가 비었다면
    return null;  // 아무것도 반환하지 않음
  }

  E item = first.item;  // 첫 번째 값 가져오기
  first = first.next;  // 그 다음 요소가 first가 됨
  n--;  // 크기 한 칸 감소

  if(isEmpty()) {  // 제거 후 큐가 빈다면
    last = null;  // last는 존재하지 않음
  }
  
  return item;
}

큐와 스택은 여러 가지 상황에서 사용할 수 있습니다. 가령 스택은 호출 순서가 명확해야 하는 경우, 예를 들어 괄호 전개나 함수 호출, 웹 브라우저의 뒤로가기 등의 상황에 대압힐 수 있습니다. 큐는 줄을 세울 수 있는 거의 모든 상황에 적용할 수 있고요. 문제 상황마다 큐와 스택 중 어떤 것을 사용하는 것이 더 적절한지 판단하여 선택할 수 있어야 합니다.

전체 코드 보기

  
// interface: Stack
public interface Queue<E> {
  int size();
  boolean isEmpty();
  void enqueue(E e);
  E dequeue();
  E first();
}

// ArrayStack
public class ArrayStack<E> implements Stack<E> {
  // member
  public static final int CAPACITY=1000;
  private E[] data;
  private int t = -1;

  // constructor
  public ArrayStack() {
    this(CAPACITY);
  }
  public ArrayStack(int capacity) {
    data = (E[]) new Object[capacity];
  }

  // methods
  public int size() { return n+1 }

  public boolean isEmpty() { return n == -1 }

  public void push(E e) {
    data[++n] = e;
  }

  public E pop() {
    if (isEmpty()) {
      return null;
    }

    E answer = data[n];
    data[n] = null;
    n--;

    return answer;
  }

  public E top() {
    if (isEmpty()) { return null }
    return data[n];
  }
}

// StackNode
public class StackNode<E> implements Stack<E> {
  // nested class: Node
  private static class Node<E> {
    // member
    private E item;
    private Node<E> next;
  }

  // member
  private Node<E> first;     
  private int n;

  // constructor
  public StackNode() {
    first = null;
    n = 0;
  }

  // methods
  public int size() { return n }

  public boolean isEmpty() { return first == null }

  public void push(E e) {
    Node<E> oldfirst = first;
    first = new Node<E>(e, oldfirst);
    n++;
  }

  public E pop() {
    E item = first.item;
    first = first.next;

    return item;
  }

  public E top() {
    if (isEmpty()) { return null }
    return first.item();
  }
}

// interface: Queue
public interface Queue<E> {
  int size();
  boolean isEmpty();
  void enqueue(E e);
  E dequeue();
  E first();
}

// QueueNode
public class QueueNode<E> implements Queue<E> {
  // nested class: Node
  private static class Node<E> {
    // member
    private E item;
    private Node<E> next;
  }

  // member
  private Node<E> first;
  private Node<E> last;
  private int n;

  // constructor
  public QueueNode() {
    first = null;
    last = null;
    n = 0;
  }

  // methods
  public int size() { return n }

  public boolean isEmpty() { return first == null }

  public void enqueue(E e) {
    Node<E> oldlast = last;
    last = new Node<E>();
    last.item = item;
    last.next = null;
    if (isEmpty()) { first = last; }
    else { oldlast.next = last; }
    n++;
  }

  public E dequeue() {
    if (isEmpty()) { return null; }
    E item = first.item;
    first = first.next;
    n--;
    if(isEmpty()) { last = null; }
    
    return item;
  }

  public E first() {
    if (isEmpty()) { return null }
    return first.item();
  }
}

cm202

데이터 구조

스택 & 큐 (Stack & Queue)

ADT: Stack

데이터 구조: ArrayStack

ArrayStack - 멤버

ArrayStack - 메소드

메소드 살펴보기

push( )

pop( )

데이터 구조: LinkedStack

LinkedStack - 멤버

LinkedStack - 메소드

메소드 살펴보기

push( )

pop( )

데이터 구조: StackNode

StackNode - 멤버

StackNode - 메소드

메소드 살펴보기

push( )

pop( )

ADT: Queue

데이터 구조: QueueNode

QueueNode - 멤버

QueueNode - 메소드

메소드 살펴보기

enqueue( )

dequeue( )

전체 코드 보기

인기 태그