[CM202] 10. 균형 탐색 트리 (Balanced Search Tree)

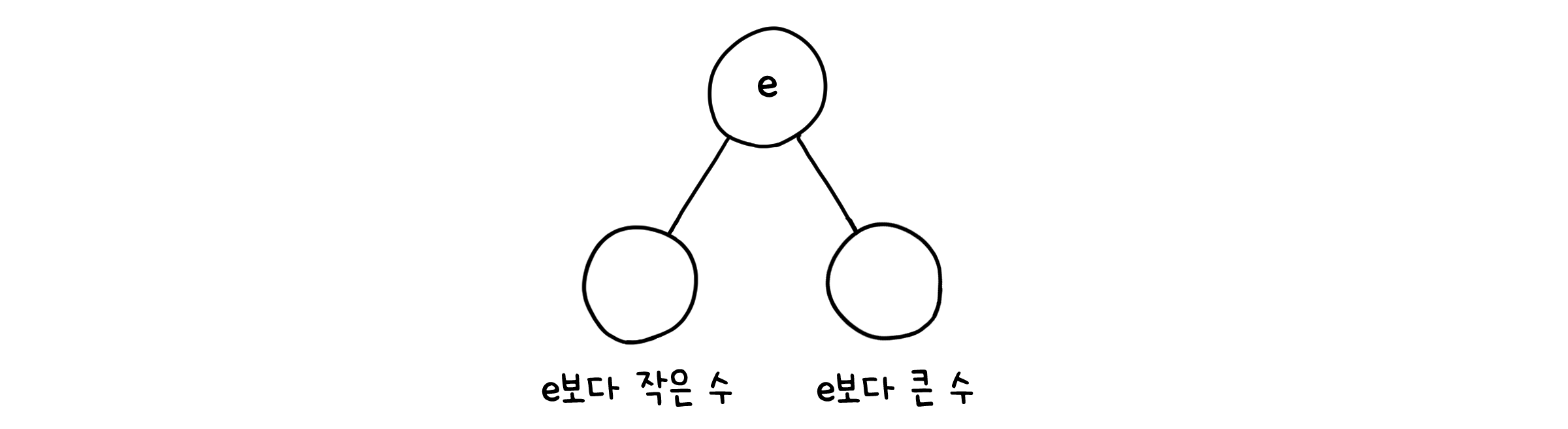
 7장에서 이야기했던 이진 탐색 트리(BST)에 대해 기억하나요? 이진 탐색 트리는 이런 구조였죠.

 탐색, 삽입, 삭제에 평균적으로 $O(logn)$의 시간이 걸리는 상당히 합리적인 데이터 구조였습니다.

 하지만 문제는, 삽입 순서가 정렬되어 들어오면 트리가 한쪽으로 기울어져 사실상 연결 리스트와 다를게 없어지는 것이었습니다. 이런 불균형 현상은 탐색트리의 계산시간을 늘리는 잠재적 문제가 되었습니다. 데이터 구조의 제일 마지막 장에서는, 이런 불균형 문제를 해결한 구조인 균형 탐색 트리들에 대해 다뤄보겠습니다.

AVL 트리 (AVL Tree)

 AVL 트리(AVL tree)는 최초 고안자인 아델슨 벨스키(Adel’son-Vel’ski)와 에브게니 랜디스(Evgenii Landis)의 이름의 첫 자를 따서 지어진 이름으로, 이진탐색 트리 중에서도 높이-균형 속성(height - balance property)를 만족하는 경우를 AVL 트리라고 부릅니다.

노드의 균형

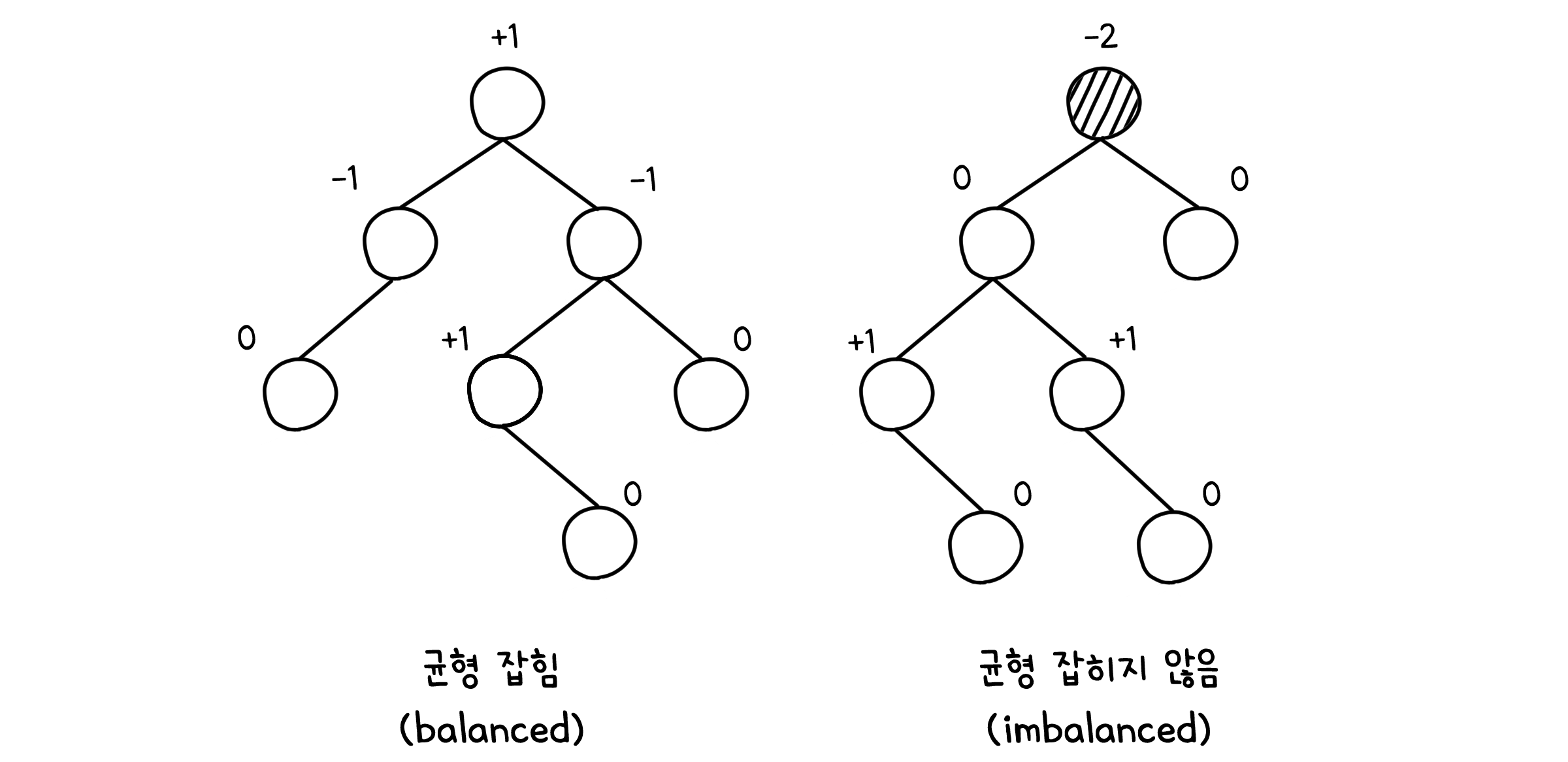
 어떤 노드에 대해 오른쪽 하위 노드의 높이에서 왼쪽 하위 노드의 높이를 뺀 값을 균형 인수(Balance factor)라고 하는데, 이 균형 인수가 -1에서 1사이이면 그 노드는 균형 잡혀 있다(Balanced)라고 합니다.

높이-균형 속성은 모든 내부 노드가 균형 잡힌 노드가 되는 것을 의미합니다. 양 쪽이 균형 있게 자라나 있어야 한다는 뜻이죠. 아래와 같은 경우 오른쪽 트리는 루트 노드의 균형 인수 크기가 1보다 커져, 불균형한 트리가 된 것을 알 수 있습니다.

 이제 균형 잡혀 있는 노드가 어떤 것인지 정의했으니, 어떤 노드가 불균형한 것인지도 알 수 있습니다. 그 노드의 균형을 바로 잡을 수도 있을테고요.

 제일 직관적인 방법은 - 돌려버리는겁니다.

트리 돌리기

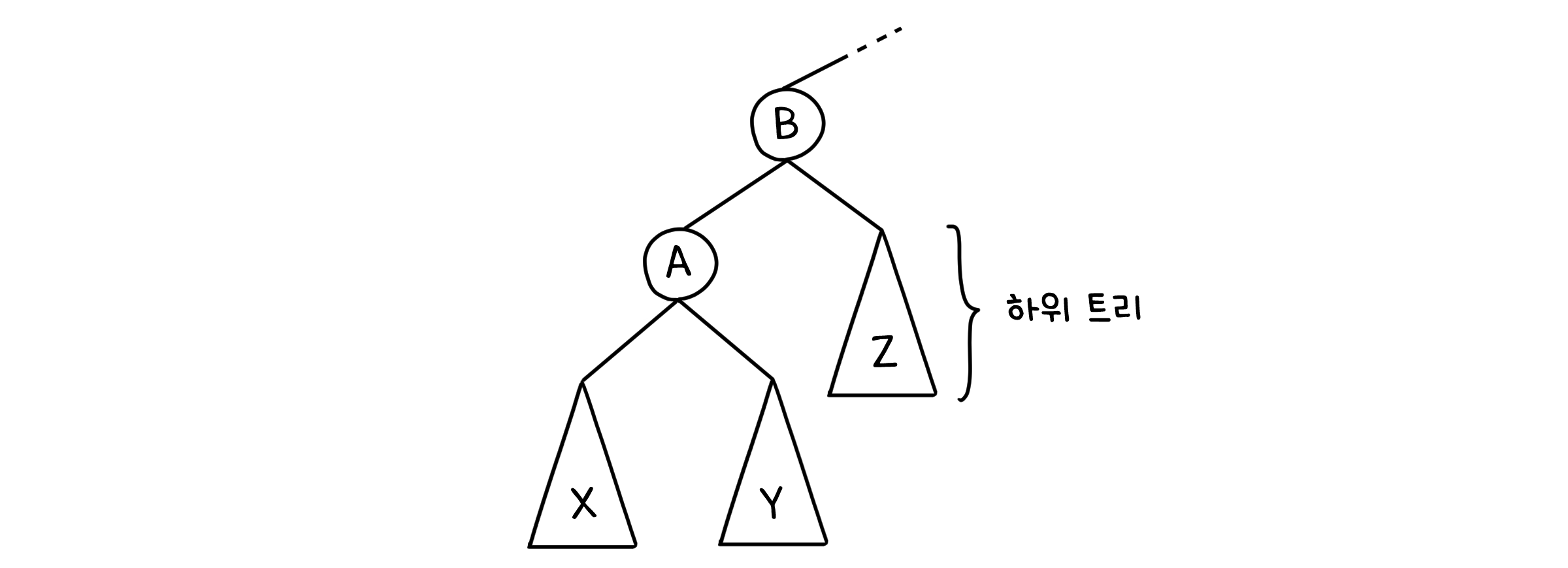
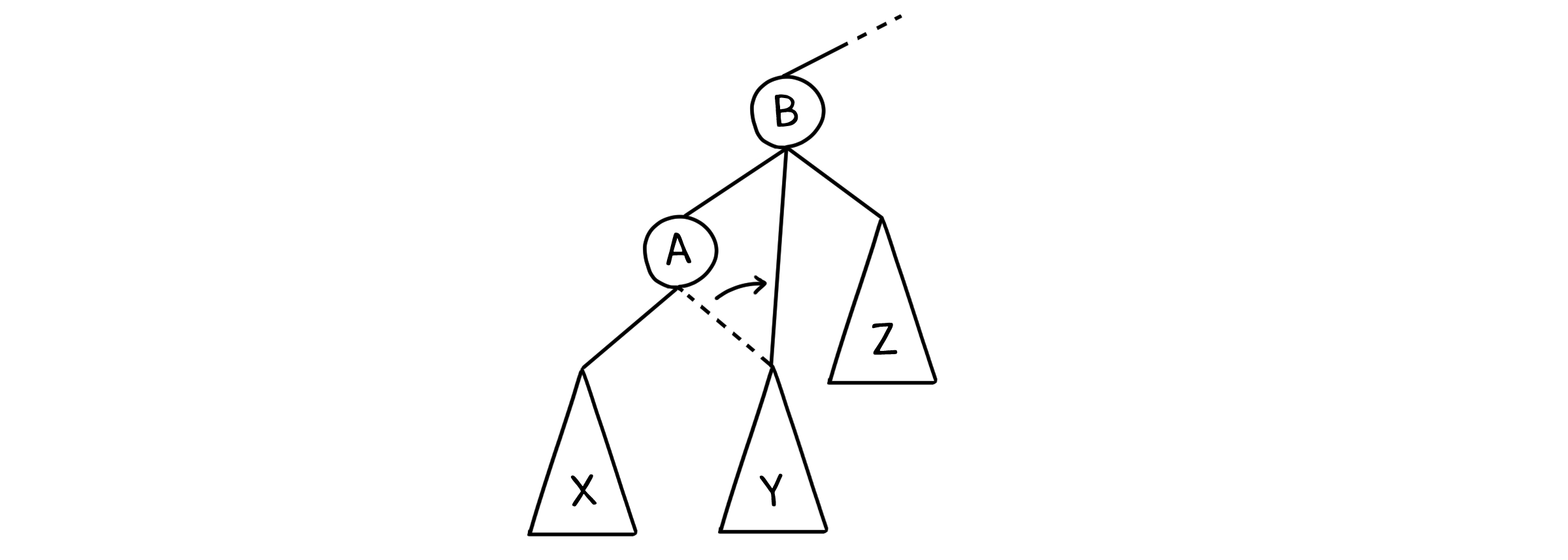
 물론 실제로 트리 전체를 돌려버리는 건 아닙니다. 최소한 탐색 트리로서의 조건을 만족시키는 선에서, 모양을 바꾸는 것이죠. 다음과 같은 하위 트리가 있다고 합시다.

 여기서 노드 A를 기준점으로 해서 오른쪽으로 한 번만 돌려보려고 해요. 우선 A의 오른쪽 하위 트리를 A의 부모인 B에다 가져다 붙입니다.

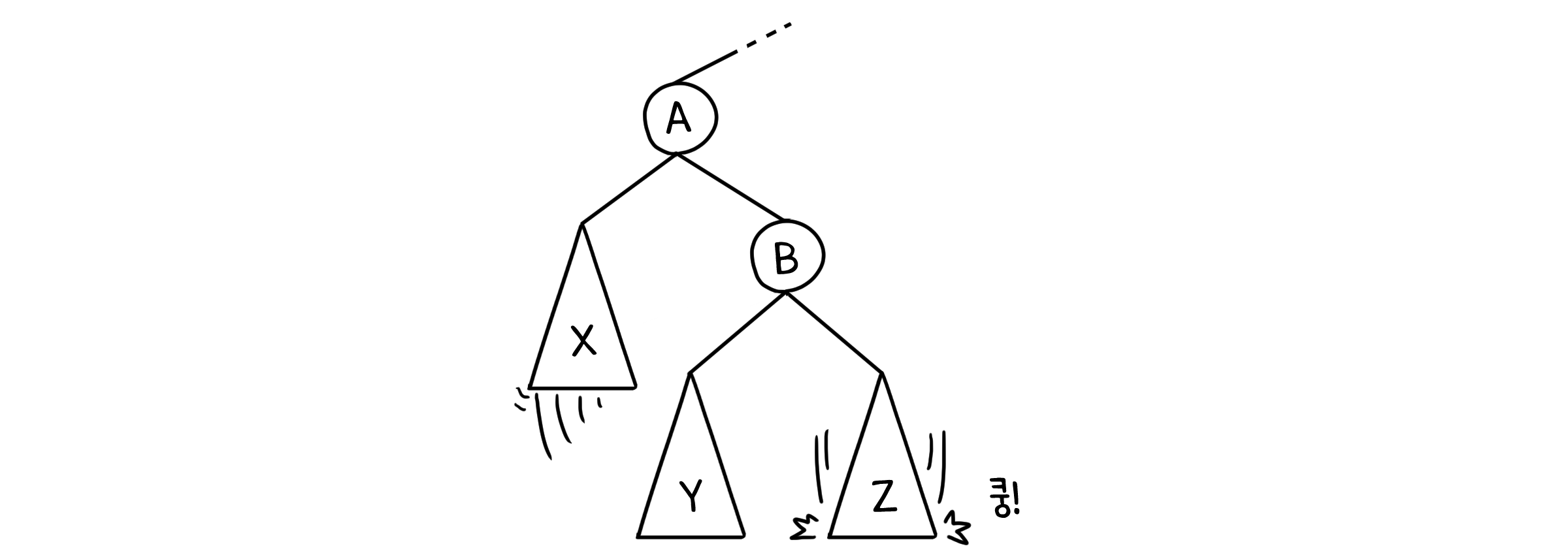
그리고 A의 부모인 B를 밑으로 끌어내려, A의 자식으로 만들어줍니다. 그러면 원래 B의 부모였던 노드는 A를 새로운 자식으로 두게 됩니다.

 이제 우리는 막 트리를 오른쪽으로 돌려버렸습니다!

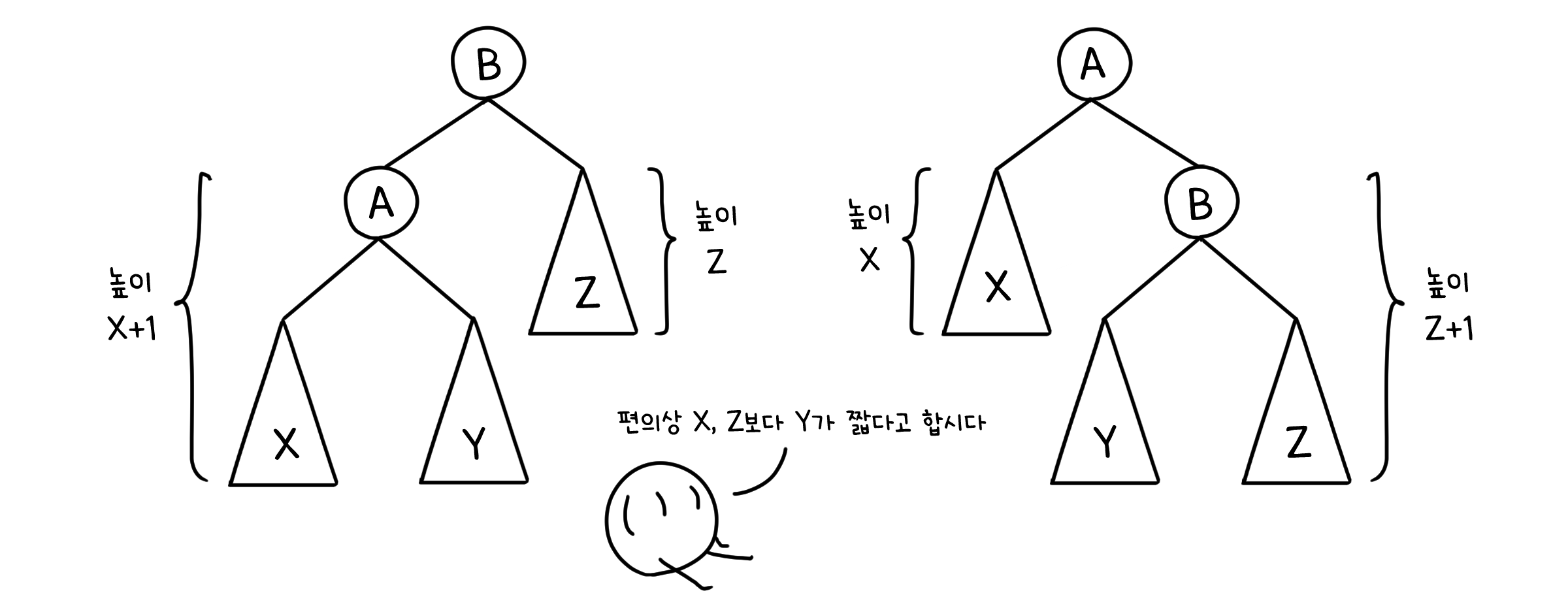
돌려서 균형 바로 잡기

 트리를 돌리는 것의 의의는, 하위 트리의 깊이를 바꿀 수 있다는 것에 있습니다. 다른 노드로 옮겨가는 하위트리를 제외한 다른 하위 트리들은 모두 그 위치가 한 칸씩 올라가거나 내려가는데, 이를 통해 원래 높이가 높던 하위 트리는 낮게, 높이가 낮은 하위 트리는 높게 변할 가능성이 있는 것이죠.

 트리 돌려버리기가 유용하게 쓰일 만한 상황은 크게 두 가지가 있습니다.

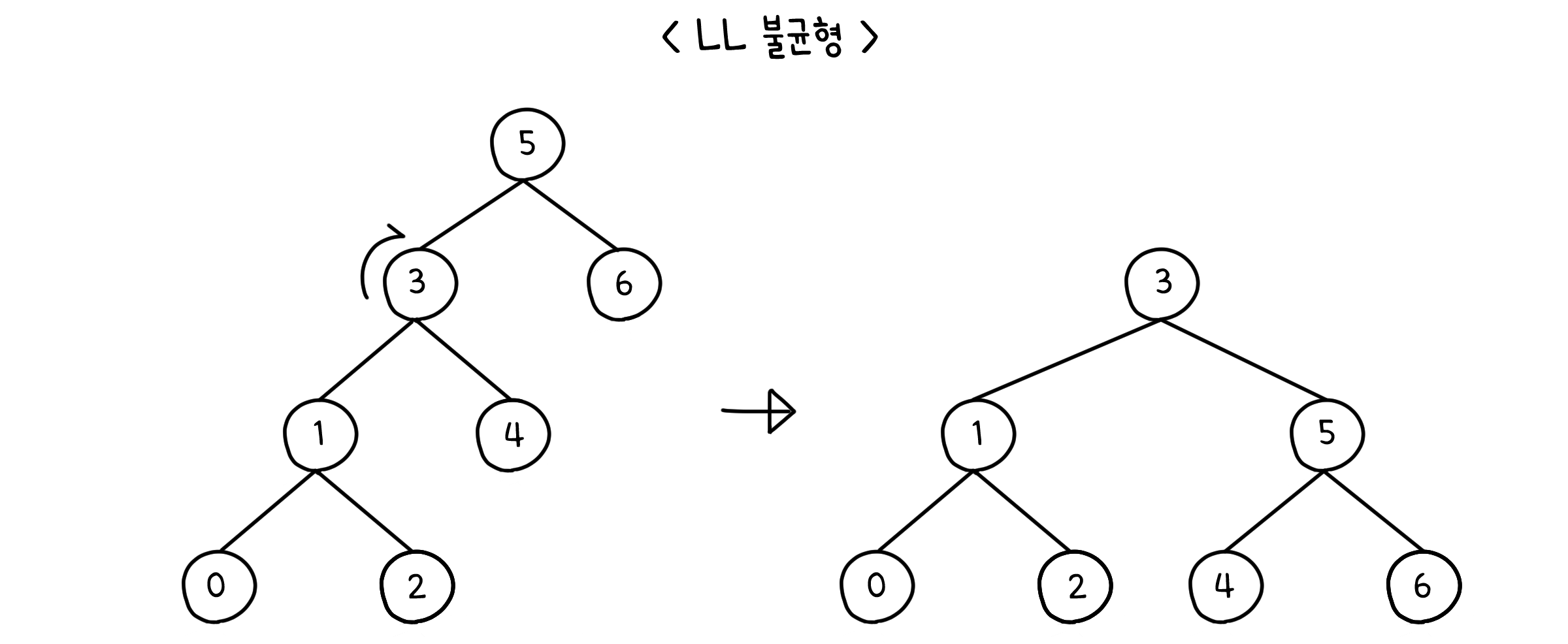
LL & RR 불균형

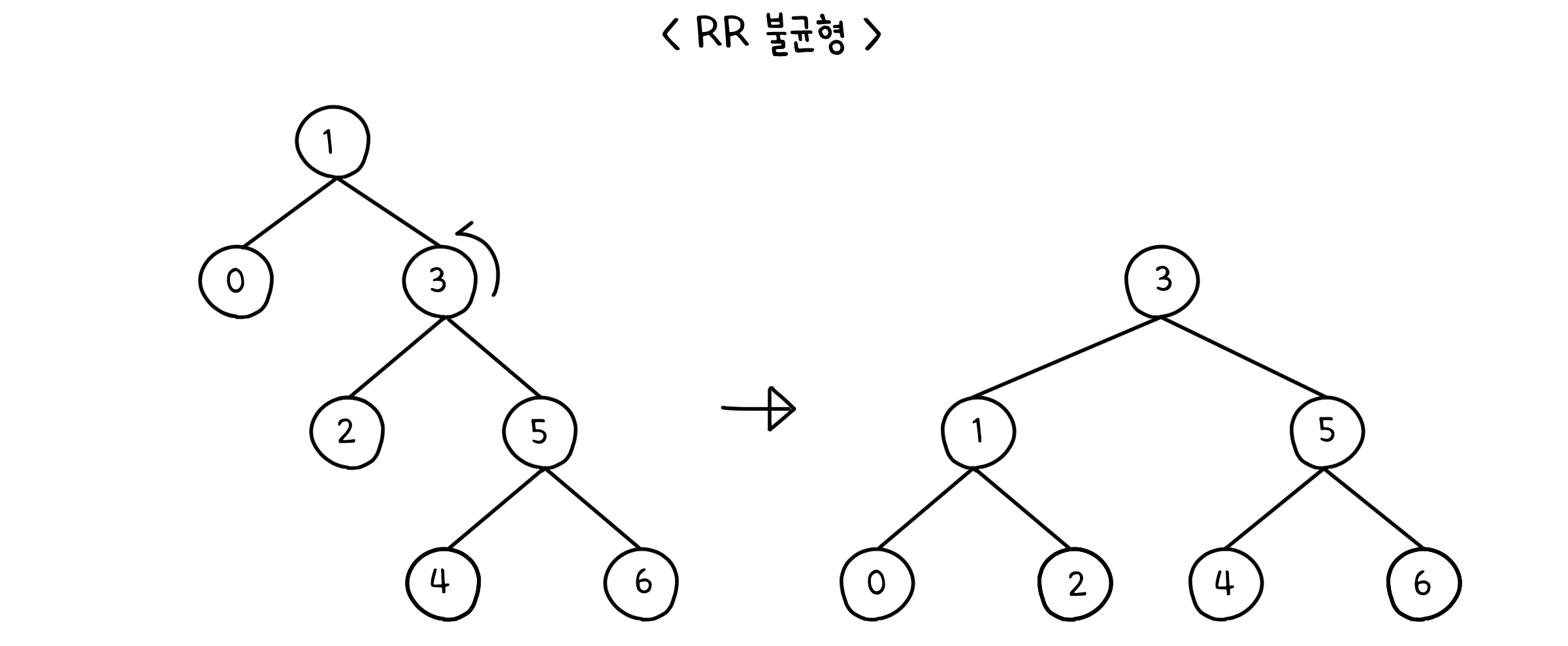
 아래와 같이 트리가 한 쪽으로 쏠려 있는 경우, 트리를 한 번만 돌려서 해결할 수 있습니다.

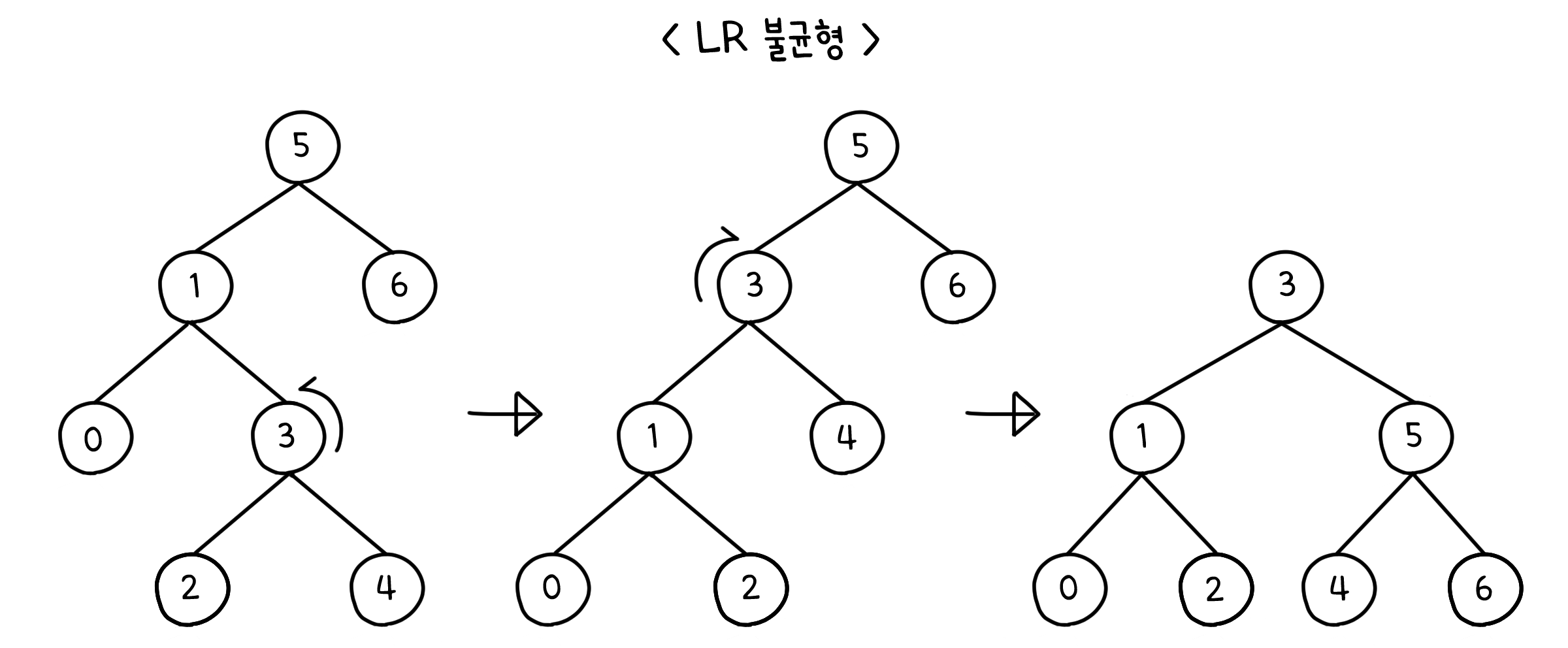
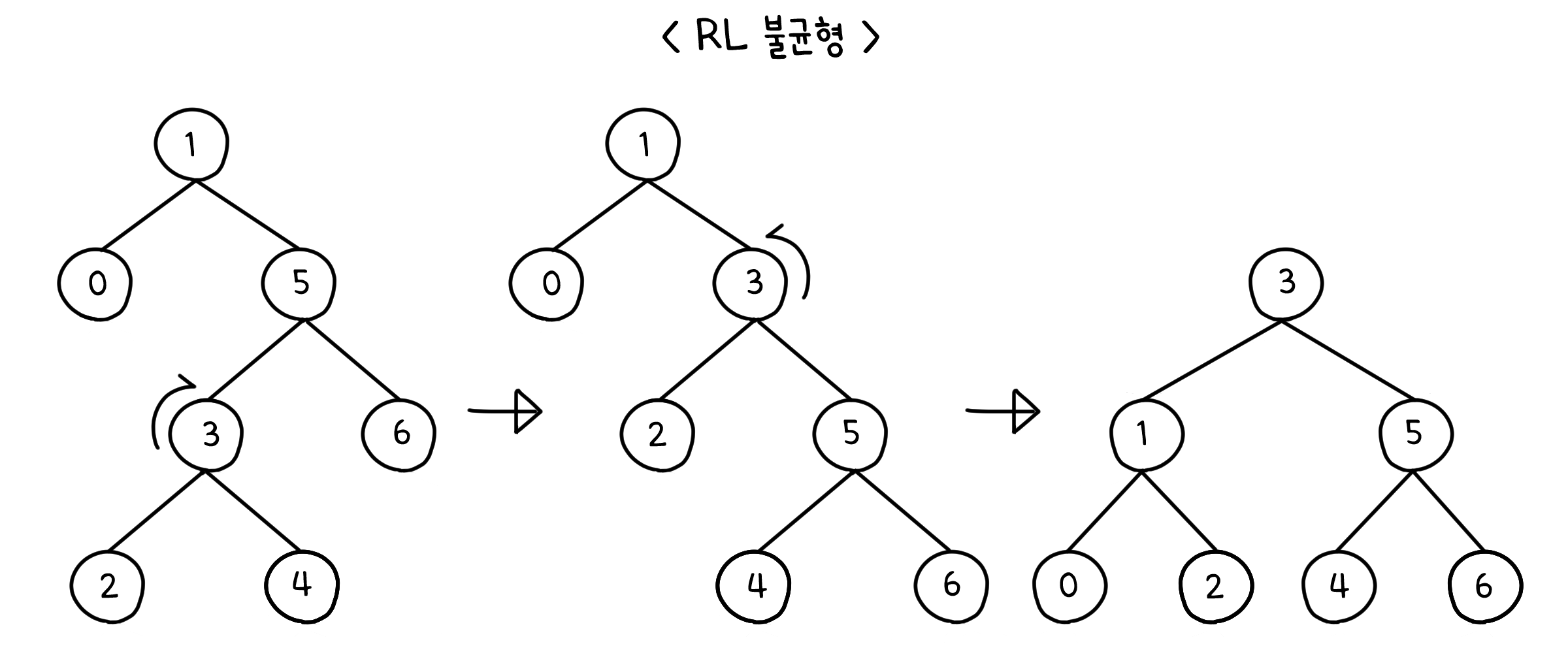
LR & RL 불균형

 아래와 같이 트리의 중간이 튀어 나온 경우는 트리를 한 번만 돌려서는 해결할 수 없습니다. 어쩔 수 없이 LL & RR 불균형 상태로 만든 후, 다시 한 번 더 돌려서 불균형을 해결해야 합니다.

 이 두 가지 경우만 신경 쓴다면, 웬만한 경우에 대해 트리의 불균형을 해결할 수 있습니다.

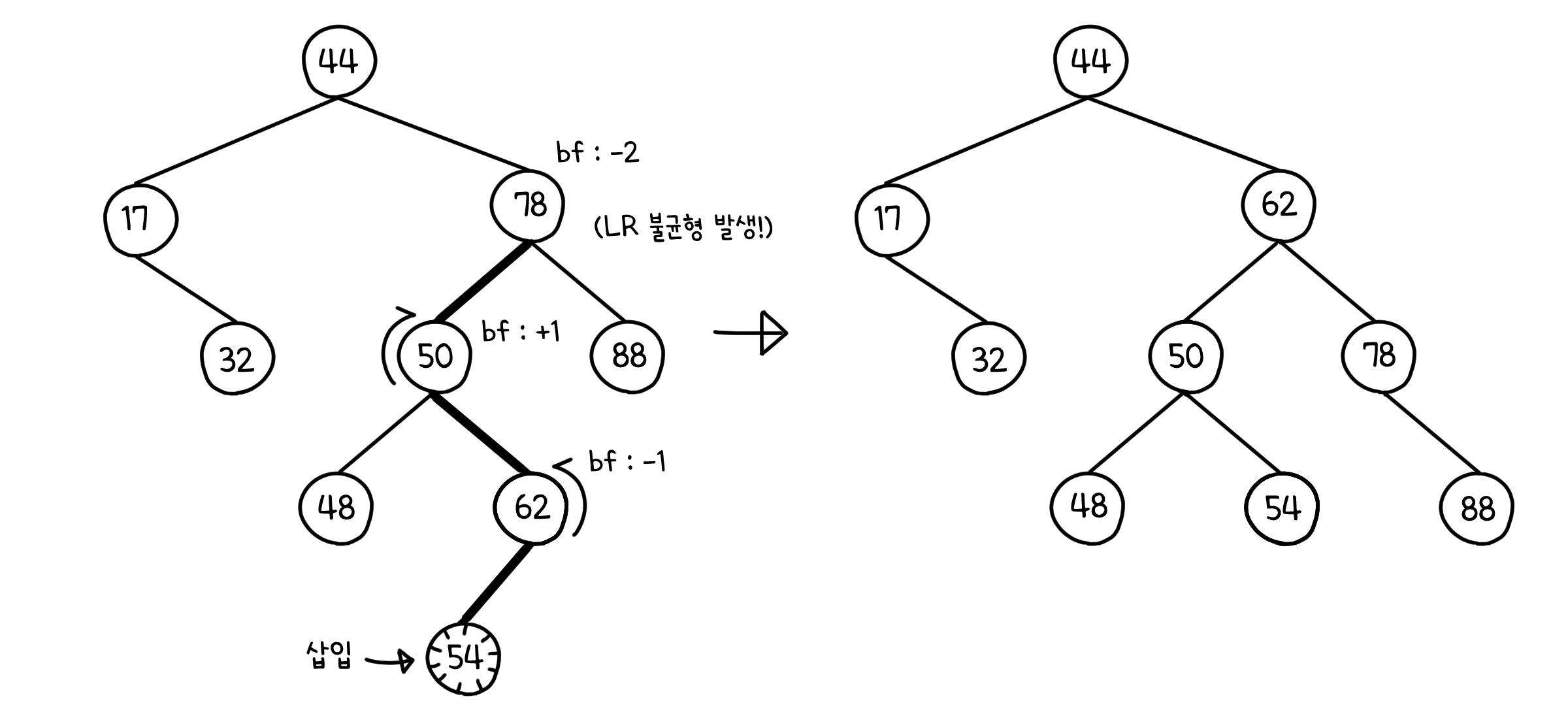
값 추가/제거

 이진 탐색 트리에 값이 추가 되거나 제거되면, 트리의 균형이 깨질 수 있습니다. 때문에 해당 작업을 할 때마다, 삭제되거나 추가된 노드에서부터 부모들을 거슬러 올라가면서 균형 인수가 올바르게 유지되는지 확인해주어야 합니다. 중간에 그 크기가 1을 벗어나는 노드가 발견된다면, 거기서 트리를 돌려버림으로서 다시 균형을 맞춰 주는 것이죠.

 AVL 트리는 루트 수준에서부터 양쪽의 균형이 맞아야 하므로, 노드가 $n$개 있을 때 그 높이는 $logn$임을 보장할 수 있습니다. 즉, 기존의 이진 탐색 트리 처럼 최악의 경우 계산 시간이 $O(n)$이 될 우려를 하지 않아도 된다는 것입니다. 게다가 매 탐색/추가/제거 후 균형 인수를 계산하는 과정도 노드 전체를 순회하는 것이 아니기 때문에, $O(logn)$의 시간을 벗어나지 않습니다. 이로서 우리는 일반적인 이진 탐색 트리보다 더 합리적인 구조를 고안해낸 셈입니다.

	평균 실행시간	최악의 경우 실행시간
이진 탐색 트리	$O(logn)$	$O(n)$
AVL 트리	$O(logn)$	$O(logn)$

2-3 트리 (2-3 tree)

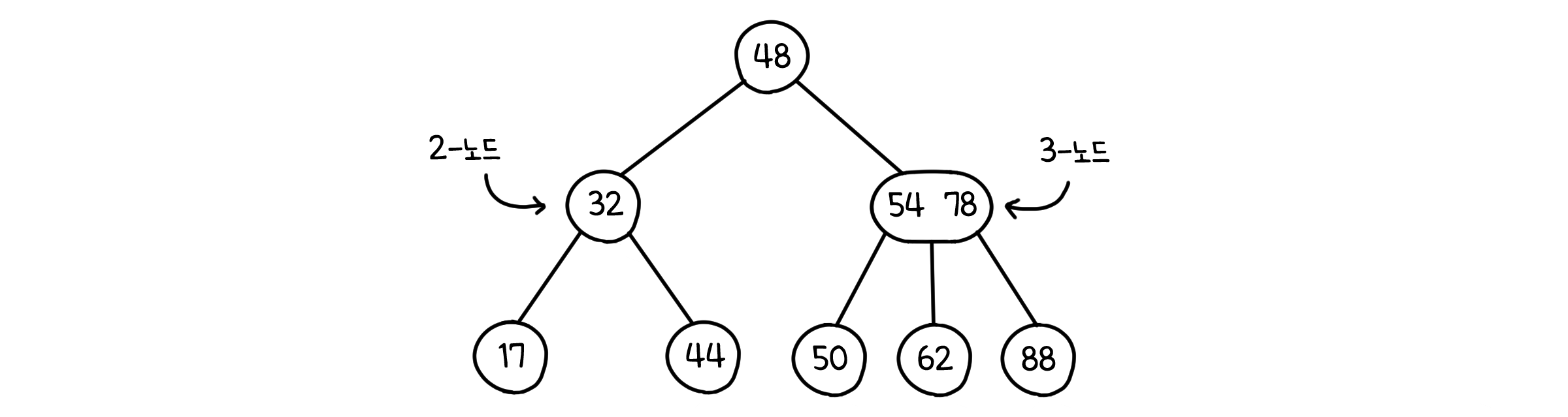
 2-3 트리(2-3 tree)는 AVL보다 약간 더 일반적인 균형 탐색 트리입니다. 가장 큰 특징은, 이진 트리의 형태를 벗어나 자식을 셋 가진 노드가 존재할 수 있다는 것입니다. 이를 3-노드(3-node)라고 하며, 원래대로 두 자식을 가지면 2-노드(2-node)라고 합니다.

 2-3 트리의 또 다른 중요한 점은, 항상 모든 잎 노드가 같은 깊이를 가질 수 있도록 만들 수 있다는 것입니다. 이것은 2-3의 노드 추가 전략이 조금 독특하기 때문입니다. 2-3트리는 일반적인 트리와는 달리, 밑에서부터 위로 자라납니다. 무슨 말이냐고요? 좀 더 자세히 살펴봅시다.

값 추가하기

 일단 트리를 하나 준비했습니다. 이제 여기에 계속 값을 넣어봅시다.

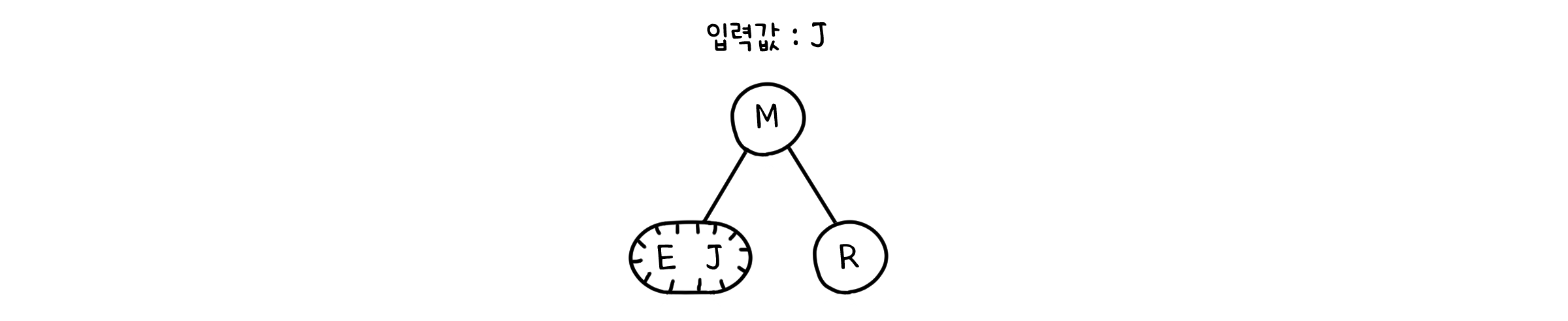
 다음 값을 넣기 위해서는 트리가 한 단계 더 깊어져야 합니다. 하지만 2-3트리에서는, 잎 노드를 3-노드로 바꿈으로서 깊이를 유지할 수 있습니다.

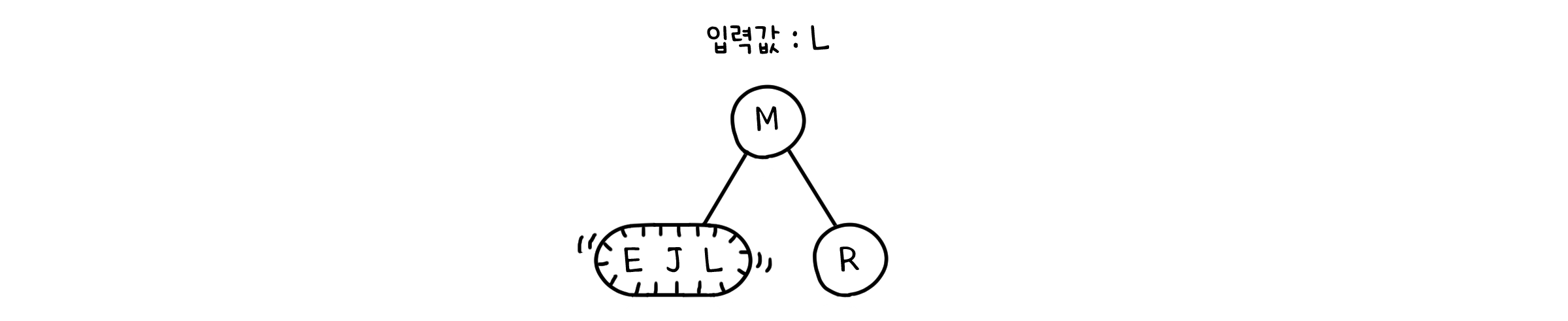
 하지만 그 다음 값도 같은 자리에 들어온다면 어떻게 될까요? 이미 잎 노드는 값 두개로 만석인데 말이죠. 여기서 2-3 트리의 전략이 시작됩니다. 우선 3-노드는 새로운 값을 받아 일시적으로 4-노드가 됩니다.

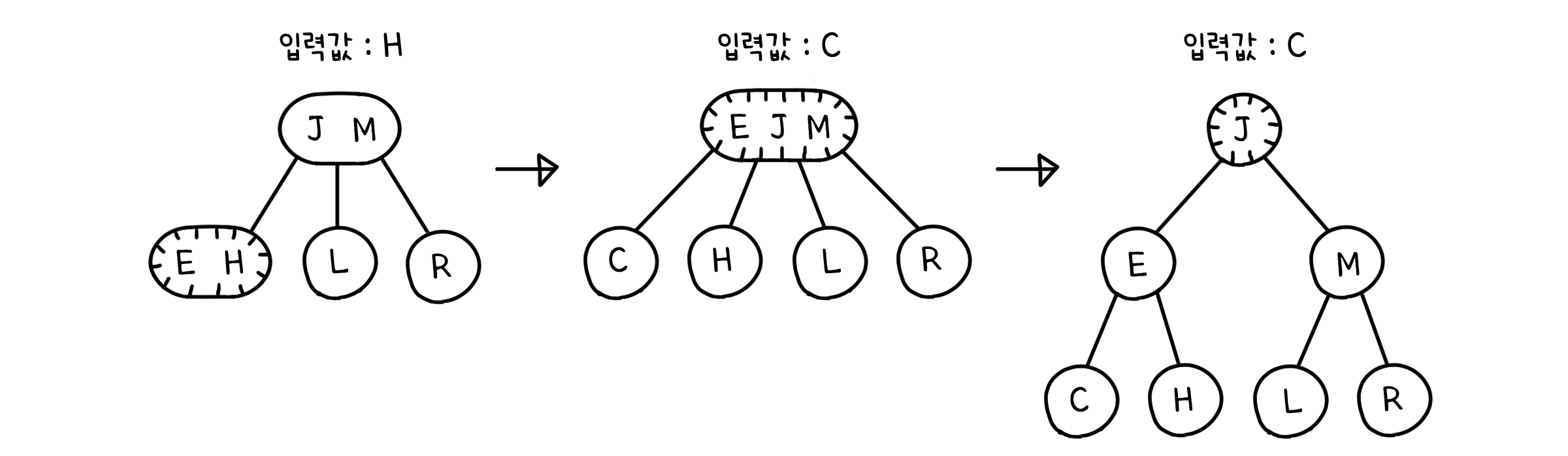
 그리고 4-노드는 자신의 가운데 값을 부모에게로 올립니다. 부모가 2-노드였다면, 3-노드로 변하겠죠. 가지는 자식도 3개가 될 것이고요.

 그러면 4-노드에 있던 나머지 두 값은 두 개의 2-노드로 분리되어 각각 부모 노드의 자식으로 들어갈 것입니다.

 자식 노드가 있는 3-노드에 값이 들어올 때도, 똑같이 4-노드를 만들고 가운데 값을 위로 올립니다. 단, 이 때는 4-노드의 네 자식들이 2-노드들에 두 개씩 들어가게 됩니다.

 이런 식으로 깊이가 깊어지려고 하면 계속해서 값들을 위로 올려 트리의 균형을 맞추게 됩니다. 2-3 트리의 계산 시간은 노드의 구성에 따라 달라집니다. 최악의 경우는 모든 노드가 2-노드로 이루어진 경우, 즉 평범한 AVL 트리일 때가 됩니다. 걸리는 시간은 $O(logn)$이 되겠죠. 최선의 경우는 모든 노드가 3-노드로 이루어진 경우입니다. 이 때는 조금 특이한 형태인 $O(log_3n)$의 시간이 걸리게 됩니다. 대강 계산해보자면, $O(0.631logn)$, 즉 최악의 경우 보다 60% 정도 까지 시간이 단축되는 것을 알 수 있습니다.

 2-3트리는 이름에서 유추할 수 있듯이 사용하는 노드의 종류를 늘려가며 2-3-4, … 와 같은 식으로 개념을 확장할 수 있습니다. 실제로 이의 연장선상에는 B 트리나 B+ 트리와 같이 더 복잡한 형태의 데이터 구조가 존재합니다. 그리고 이렇게 발전된 형태는 데이터베이스나 파일시스템에서 사용할 수 있을 만큼 뛰어난 성능을 발휘할 수 있게 됩니다.