[CM201] 08. 경로와 회로 (Path & Circuit)

 이제 진짜로 여행을 떠날 시간입니다! 바로 전까지 그래프에 대해 살펴보았으니, 지도의 길들을 그래프로 간단히 표현할 수 있겠죠.

 하지만 그래프만으로는 충분하지 않습니다. 중요한건 우리가 갈 길을 찾는 것이니까요. 이를 위해서는, 그래프에서 좀 더 특수한 형태를 생각해보아야 할 것입니다.

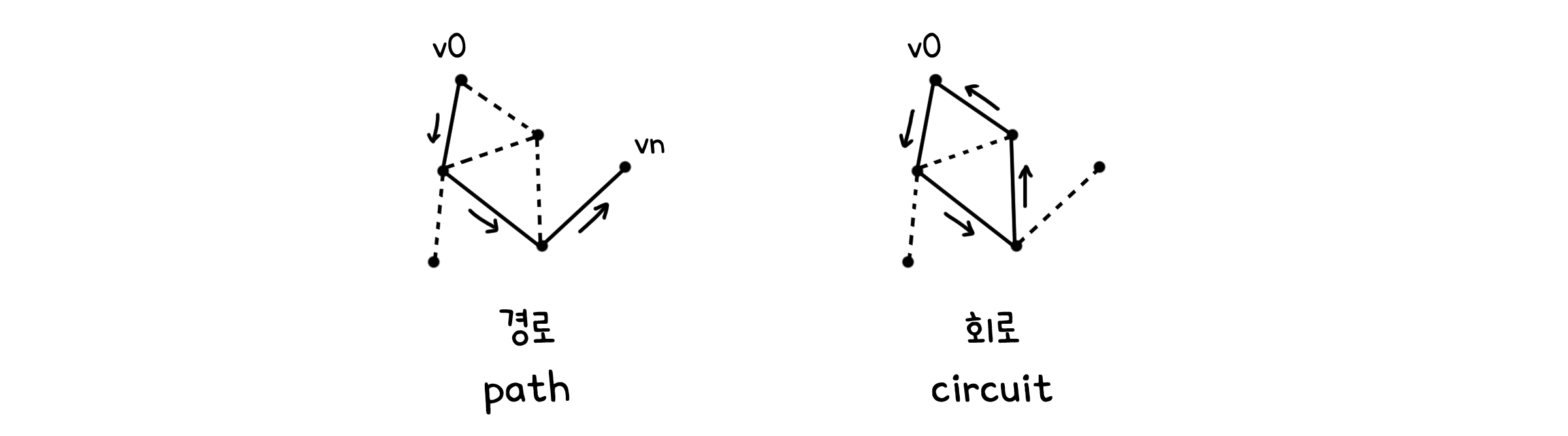
경로 (path)

 그래프 $G=(V, E)$에 속한 두 점 $v_0, v_n \in V$ 사이의 경로(Path)는 점을 연결하는 선과 그 선으로 연결된 점을 번갈아가며 배열한 순서를 나타냅니다. 만약 출발점과 도착점이 같다면($v_0$에서 $v_0$), 이를 회로(Circuit)라고 합니다.

\[(v_0, \; e_1, \; v_1, \; e_2, \; ..., \; e_n, \; v_n)\]

 경로와 회로 모두 중복되는 선이 없는 단순한 형태를 단순 경로(Simple path)와 단순 회로(Simple circuit)라고 하는데, 특히 단순회로는 사이클(Cycle)이라고도 부릅니다. 만약 여기에 선 끼리 중복되는 점도 없다면(=한 번 방문한 점을 다시 방문하지 않는다면), 단순 사이클(simple cycle)이라고 합니다.

어떤 문헌에서는 용어를 혼용하기도합니다. ‘path’와 ‘circuit’ 대신 ‘walk’와 ‘closed walk’를 쓰기도 하고, ‘simple path’를 ‘trail’이라고 쓰기도 합니다. 여기서는 위에서 정의한 용어를 기준으로 설명을 이어나가도록 하겠습니다.

 만약 어떤 그래프에 대해서 아무 두 점을 잡아도 그 사이에 경로가 존재한다면, 그 그래프는 연결되어 있다(Connected)고 말합니다.

다리 건너기

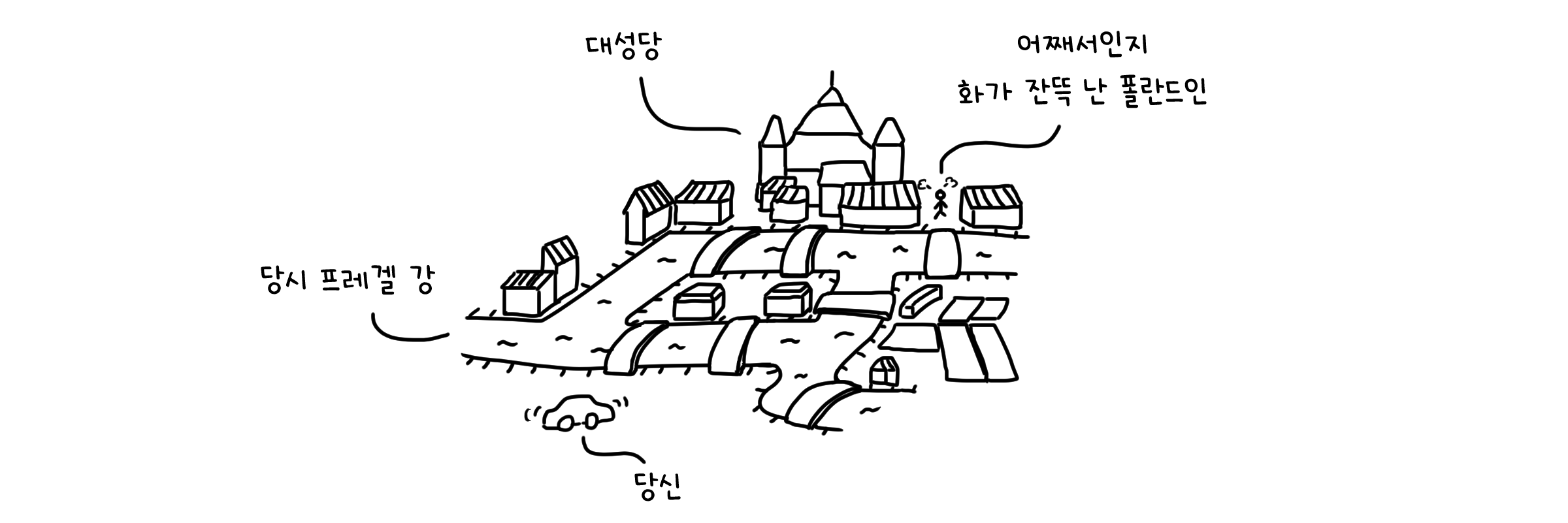
 어쩌다보니 러시아에 도착하게 되었습니다. 칼닌그라드라는 곳이군요. 여기서 조금만 시간을 앞으로 감아봅시다… 한 18세기 정도로요.

 이 때는 프로이센 왕국이 존재했습니다. 동프로이센에 속한 이 지역은, 프레겔 강이라는 작은 강이 두 개의 하중도를 끼고 있는 아름다운 곳입니다. 이 독특한 지형 때문에 육지와 하중도를 연결하는 여러 다리들이 놓여져 있었어요. 여러분은 여유로운 관광을 위해 모든 다리들을 한 번씩 지나가면서 도시를 둘러보기로 합니다.

 그런데 이게 쉽지가 않습니다. 수상함을 느낀 여러분은 이곳의 지명을 살펴보고 깨닫게 됩니다. 이곳이 그 유명한…

 …쾨니히스베르크의 다리라는 것을요.

오일러 경로 (Euler path)

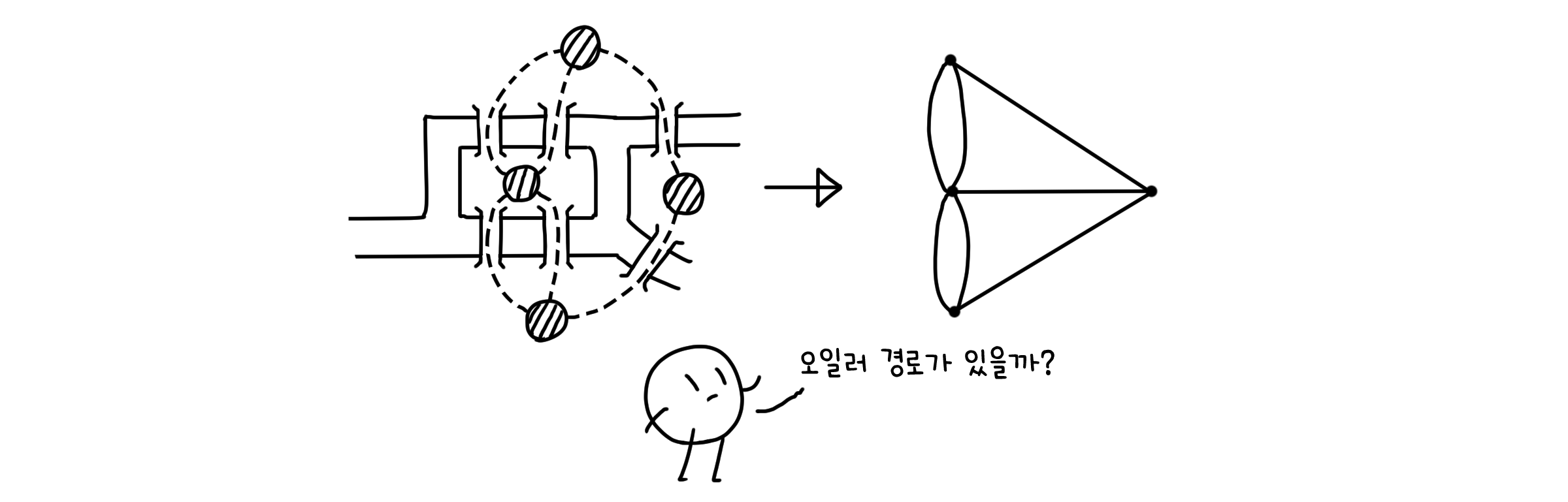
 쾨니히스베르크의 다리가 있는 지역을 그래프로 표현해볼 수 있을 것입니다. 육지를 점, 다리를 선이라고 생각한다면요. 우리의 목표는 모든 다리를 정확히 한 번만 거쳐 모든 다리를 지나가는 것이었으니, 그래프에서 모든 선을 포함하는 단순 경로(중복되는 선이 없는 경로)를 찾는 문제로 재정의할 수 있습니다. 이러한 조건을 만족하는 경로를 오일러 경로(Euler path)라고 합니다. 만약 시작점으로 돌아와야 한다면, 오일러 회로(Euler circuit)가 되겠죠.

오일러 회로 찾기

 우리는 몇 가지 간단한 정리를 통해 그래프가 오일러 경로나 회로를 가질 수 있는지 판단할 수 있습니다. 이런 식으로요.

Theorem 1.
그래프가 연결되어 있고 두 개 이상의 점을 가질 때, 그 그래프는 모든 점의 차수가 짝수일 때만 오일러 회로를 가진다. 그 반대도 성립한다.

오일러 회로 찾기 - 증명

 위 정리는 필요충분조건이기 때문에, 양방향 모두 성립함을 보여야 합니다.

1. 그래프가 오일러 회로일 때

 회로는 방문하는 점을 한 번씩 들어가고 나오기 때문에, 방문 횟수당 2의 차수를 추가합니다. 따라서 모든 점의 차수는 반드시 2의 배수를 가집니다. $\Box$

2. 그래프의 모든 점이 짝수 차수를 가질 때

 수학적 귀납법으로 증명할 수 있습니다.

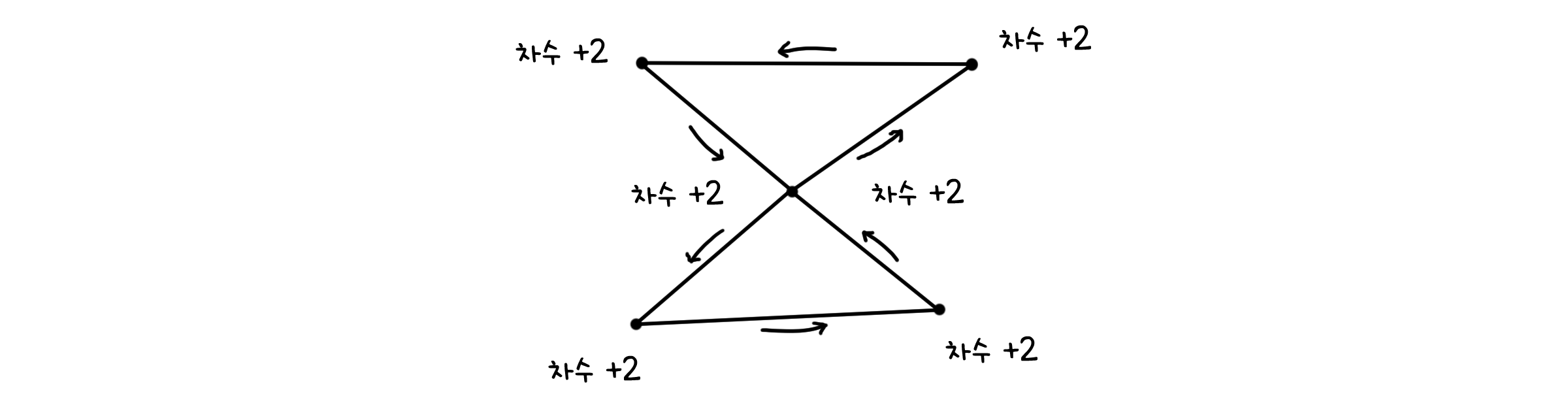
 1. 기본 단계. 그래프의 선이 두 개인 경우입니다(선이 0, 1개인 경우는 시작점과 도착점이 동일하게 고정되므로 자명합니다). 선이 두 개일 때 연결되면서 모든 차수가 짝수개인 그래프는 아래와 같은 모양을 생각할 수 있겠습니다. 이 경우 오일러 회로를 가질 수 있다는 것을 바로 알 수 있습니다.

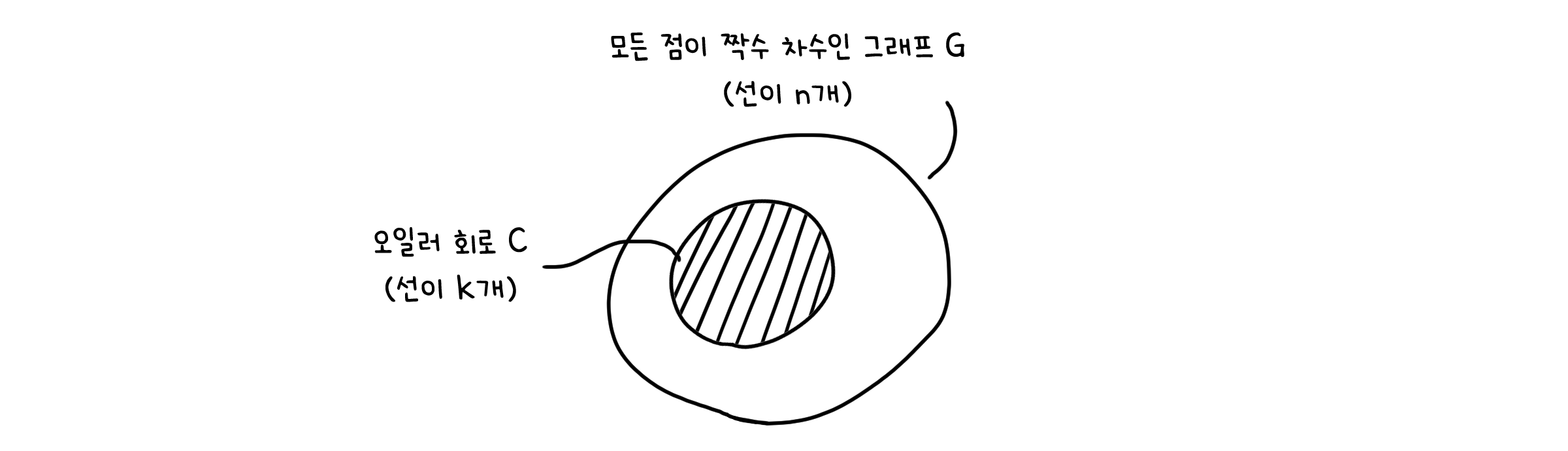
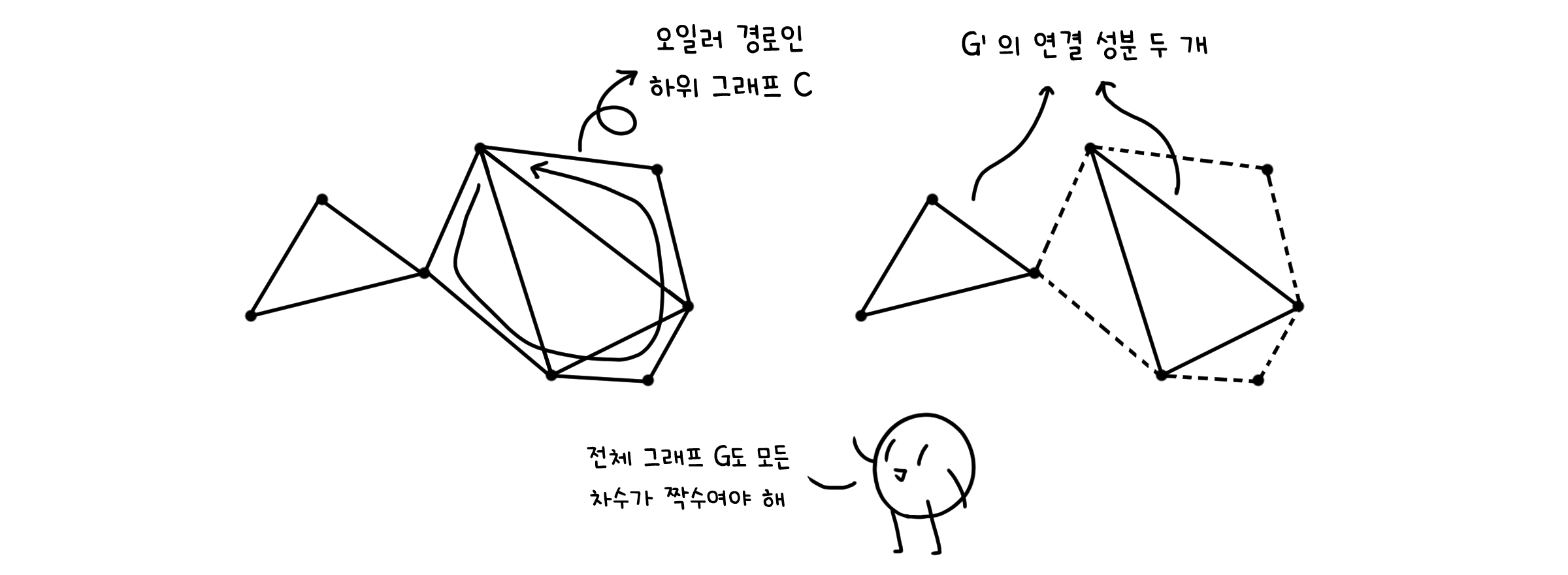
 2. 귀납적 단계. 그래프의 선이 n개인 경우 입니다. 이 그래프를 $G$라고 하겠습니다. $G$의 하위 그래프 중에서 연결되어 있고 모든 점의 차수가 짝수인 그래프를 $C$라고 둡니다. 이제 $C$의 선이 k개(k < n)일 때, 오일러 회로를 가진다고 가정합시다. 이 때 $G$ 또한 오일러 회로를 가짐을 보이면 됩니다. 여기서 또 두 가지 경우를 나눌 수 있습니다. 점이 두 개일 때와, 세 개 이상일 때로요.

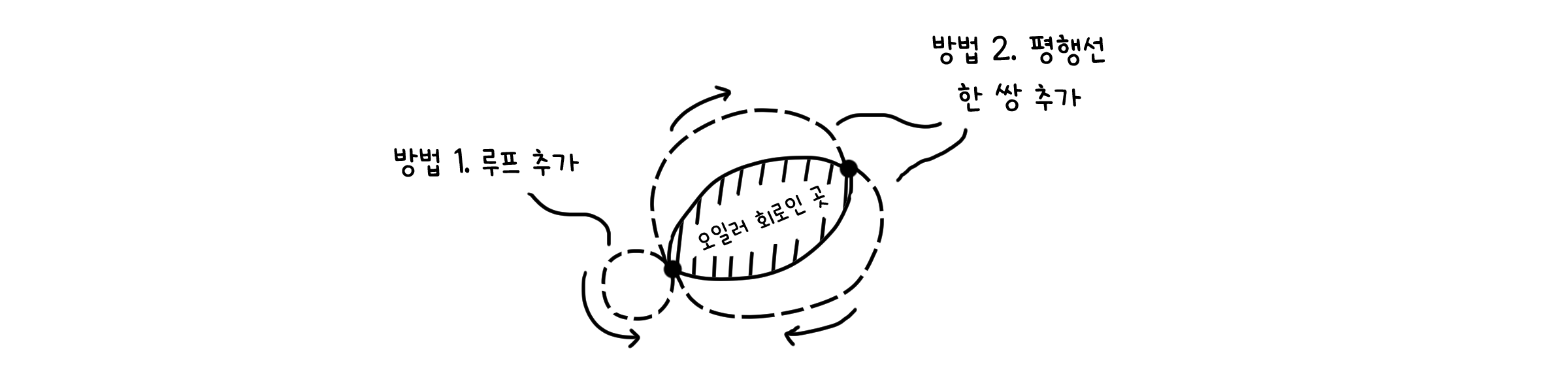
 2.1. 점이 두 개일 때. $C$에 선이 추가되는 경우, 각 점의 차수가 짝수가 되도록 유지하는 방법은 두 가지가 있습니다. 한 점에 루프가 하나 추가되거나, 두 점을 왕복하는 평행선 한 쌍이 추가되는 경우입니다. 두 가지 경우 모두 오일러 회로를 보일 수 있습니다.

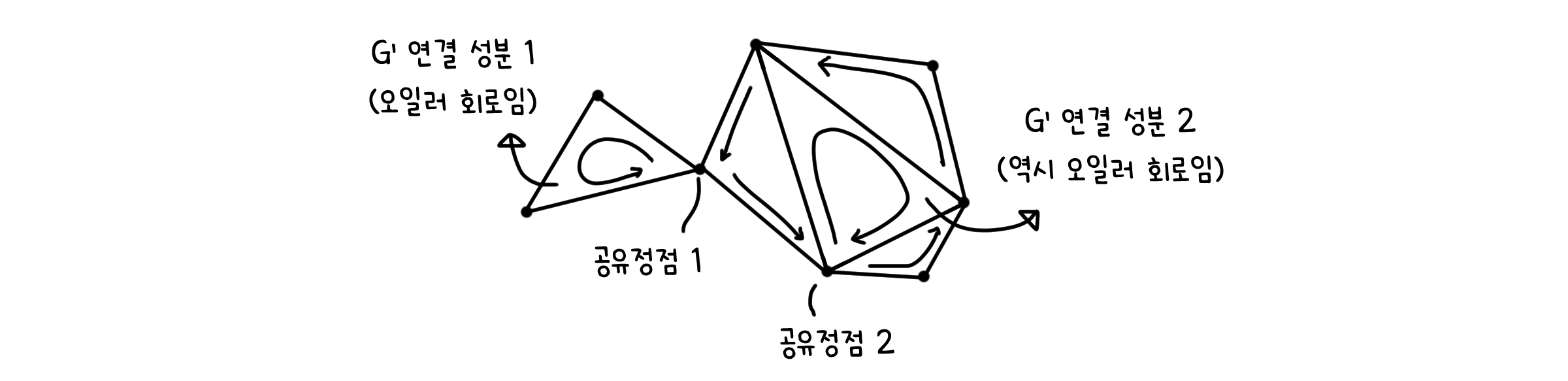
 2.2. 점이 세 개 이상일 때. $G$의 모든 점의 차수는 짝수가 되어야 하고 $C$의 모든 점의 차수도 짝수이므로, $G$에서 $C$의 선을 뺀 그래프 $G’$또한 모든 점이 짝수 차수를 가질 것입니다. 또한 $G’$ 자체는 모두 연결되어 있지 않을 수 있지만, $G$가 연결된 그래프였기 때문에 $G’$의 연결 부분들은 각각이 또 다른 연결된 그래프임을 알 수 있습니다.

 각 연결부분의 선의 개수 또한 전체 선의 개수 n보다는 작습니다. 따라서 앞서 세운 가정(선의 개수 k가 k < n일 때 오일러 회로를 가짐)에 따라 이들도 각각 오일러 회로를 가지게 됩니다. 그렇다면, 우리는 이제 $G$를 이루는 모든 성분들이 오일러 회로를 가진다는 것을 토대로 하나의 큰 오일러 회로를 그릴 수 있게 됩니다. 서로 공유하는 정점이 있으면, 그 점에서 회로 하나를 순회하고 곧바로 경로를 이어나갈 수 있으니까요.

 따라서, 수학적 귀납법에 따라 그래프의 모든 점이 짝수 차수를 가지면 그래프는 오일러 회로를 가짐을 보일 수 있습니다. $\Box$

오일러 경로 찾기

 이제 오일러 회로가 되기 위한 조건을 알았으니, 회로까지는 아니어도 경로 정도는 가질 수 있는 조건도 찾을 수 있습니다.

Theorem 2.
그래프가 연결되어 있을 때, 정확히 두 개의 점만 홀수 차수를 가진다면, 회로가 아닌 오일러 경로를 가진다. 그 반대도 성립한다.

오일러 경로 찾기 - 증명

 위 정리 또한 필요충분조건이기 때문에, 양방향 모두 성립함을 보여야 합니다.

1. 그래프가 회로가 아닌 오일러 경로일 때

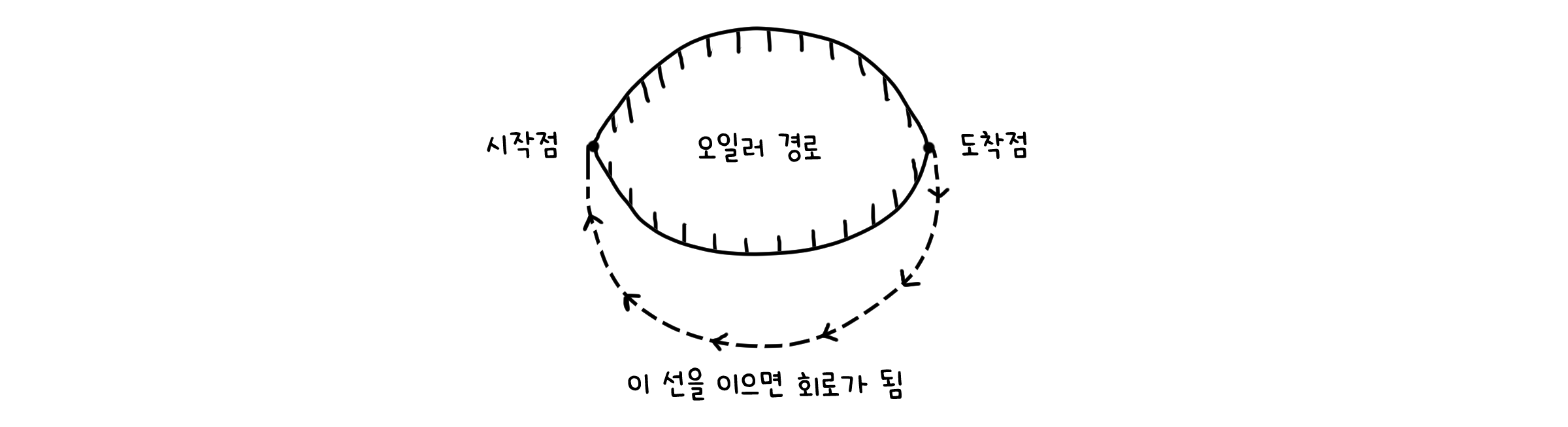
 오일러 경로이지만 오일러 회로가 아니라면, 그래프 내의 모든 선을 지나가면서도 시작점과 도착점이 같은 점에 있어서는 안됩니다. 이는 곳 시작점과 끝점을 하나의 선으로 연결하면 오일러 회로가 됨을 의미합니다. 앞선 정리에 따라 오일러 회로는 모든 점이 짝수 차수를 가집니다. 여기서 시작점과 도착점을 잇는 선을 제거하면 두 점의 차수는 1 감소하므로, 홀수 차수를 가지게 됩니다. 따라서 모든 점에서 단 두 점 만이 홀수 차수를 가지게 됩니다. $\Box$

2. 그래프의 두 점 만이 홀수 차수를 가질 때

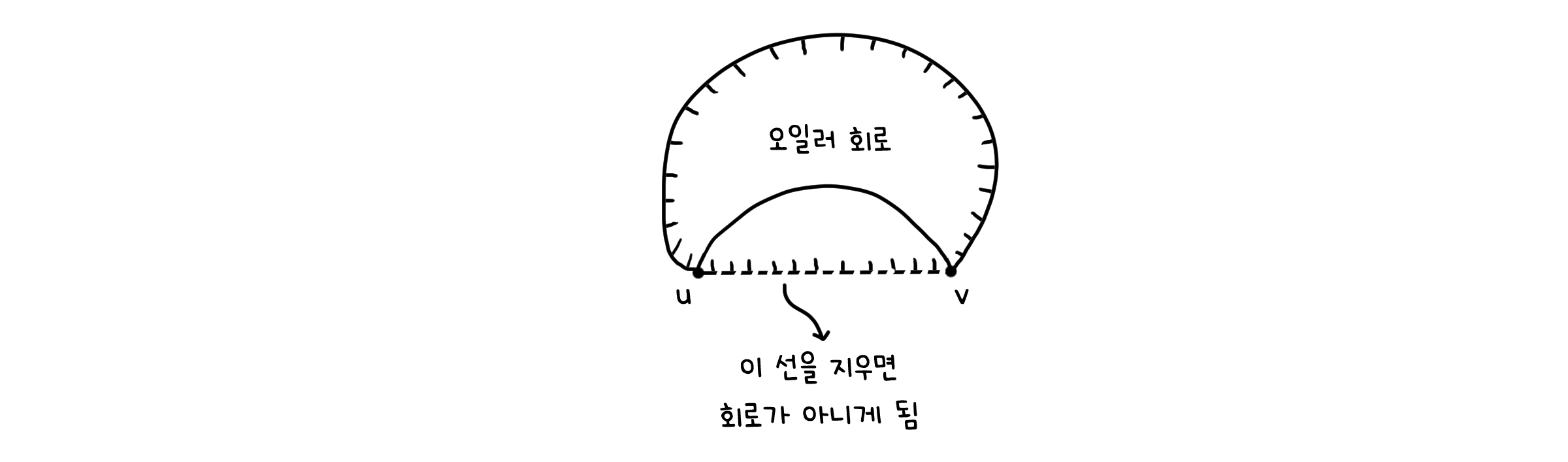
 그래프에서 홀수 차수를 가진 두 점 $u, v$를 잇는 선을 하나 더 추가한 그래프 $G’$을 생각해봅시다. $G’$은 연결되어 있으며 모든 점의 차수가 짝수이므로, 오일러 회로를 가진다고 말할 수 있습니다. 그럼 이제 다시 $u, v$를 이은 선을 제거해봅시다. 오일러 회로였던 $G’$는 모든 선을 순회하는 회로를 그릴 수 있었지만 $(u, v)$선이 하나 빠졌으니, $u$에서 시작해 $v$까지 도달했으나 마지막에 다시 $u$로 갈 수 없는 순회 경로가 만들어지게 됩니다. 따라서, 원래 그래프는 회로가 될 수 없는 오일러 경로를 가지게 됩니다. $\Box$

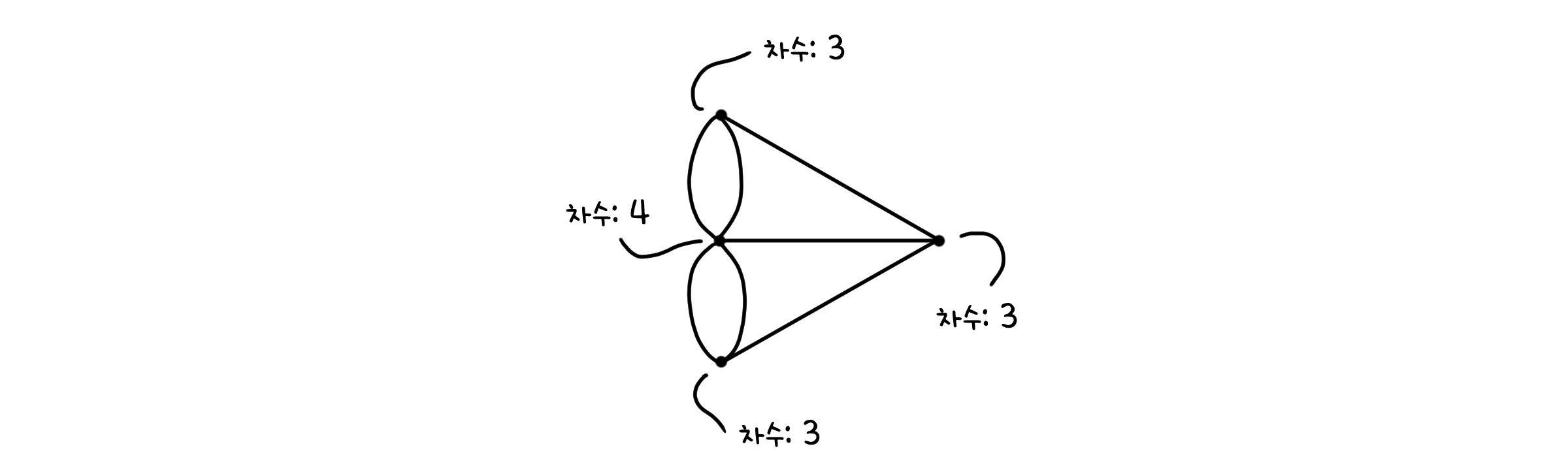
 그래서, 결국 우리는 쾨니히스베르크의 다리들을 모두 건널 수 있었을까요? 다시 한번 그래프를 살펴봅시다.

 점의 차수들을 모두 세어보면, 홀수 차수의 점이 세 개나 있군요. 오일러 경로가 되기 위한 조건인 두 개의 홀수 차수 점보다 많아졌으니, 애석하게도 다리를 한 번씩 건너기는 글러버렸습니다.

 하지만, 어쩌면 다른 기준으로는 순회할 수 있을지도 모릅니다…

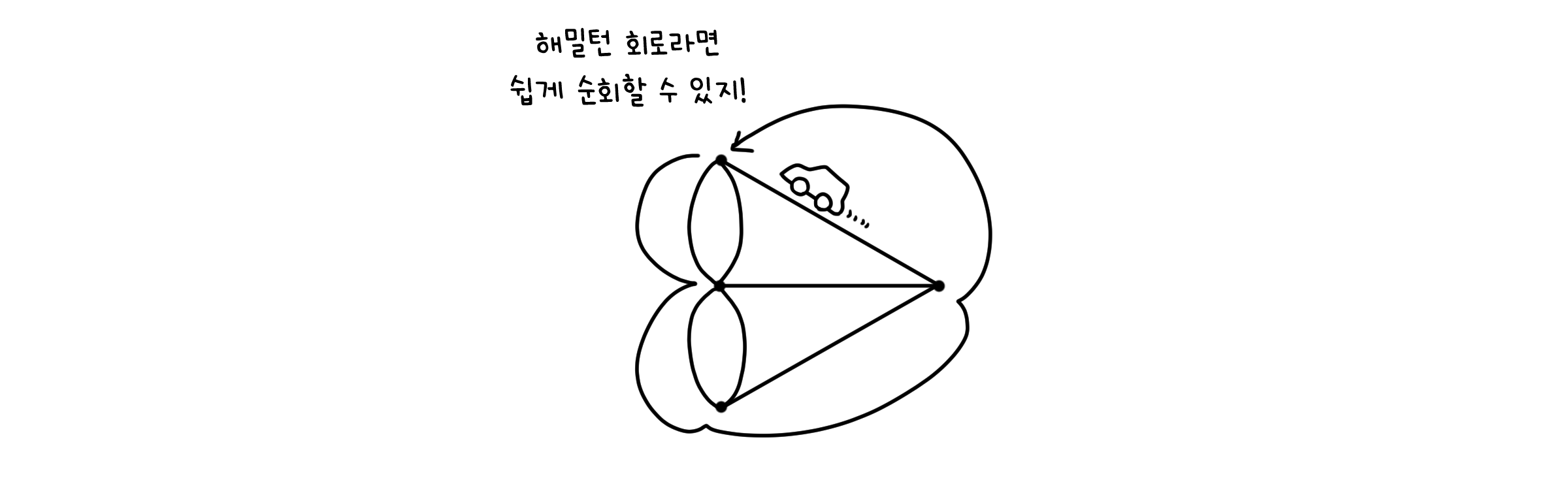
해밀턴 경로 (Hamilton path)

  헤밀턴 경로는, 오일러 경로와는 반대로 그래프에서 모든 점을 중복 없이 포함하는 경로를 찾는 문제입니다. 겹치지 않아야 하는 요소가 선에서 점으로 바뀐 셈이죠. 쾨니히스베르크의 문제에서 조금 변형시킨다면, 모든 종류의 육지를 한 번씩만 밟으면서 순회하는 문제가 될 수 있겠습니다.

해밀턴 회로 찾기

 해밀턴 회로를 가지기 위한 조건은 쉽게 찾을 수 있습니다. 각 정리의 증명은 여러분들을 위해 남겨 놓을게요.

Theorem 3.
점의 개수가 3개 이상인 완전 그래프 $K_n$은 해밀턴 회로를 가진다.

Theorem 4. 디랙의 정리 (Dirac’s theorem)
점의 개수가 $n \geq 3$ 이상인 그래프 $G$에 대해 모든 점의 차수가 최소 $n/2$개를 만족한다면, $G$는 해밀턴 회로를 가진다.

Theorem 5. 오어의 정리 (Ore’s theorem)
점의 개수가 $n \geq 3$ 이상인 그래프 $G$에 대해 모든 인접하지 않은 두 점 $u, v$의 차수 합이 $n$ 이상이면($deg(v) + deg(u) \geq n$), $G$는 해밀턴 회로를 가진다.

 정리의 형태를 보면 짐작할 수 있듯이, 해밀턴 회로는 의외로 명확한 필요충분조건이 밝혀지지 않았습니다. 즉, 그래프가 해밀턴 회로를 가진다고 해서 항상 위 정리들의 조건을 가지지 않는다는 뜻입니다.

해밀턴 회로에 대한 몇 가지 문제들

나이트의 여행 (Knight’s tour)

 나이트는 체스의 기물 중 하나로, 가로 두 칸 세로 한 칸(혹은 그 반대) 만큼 전진할 수 있는 독특한 행마법을 가지고 있습니다.

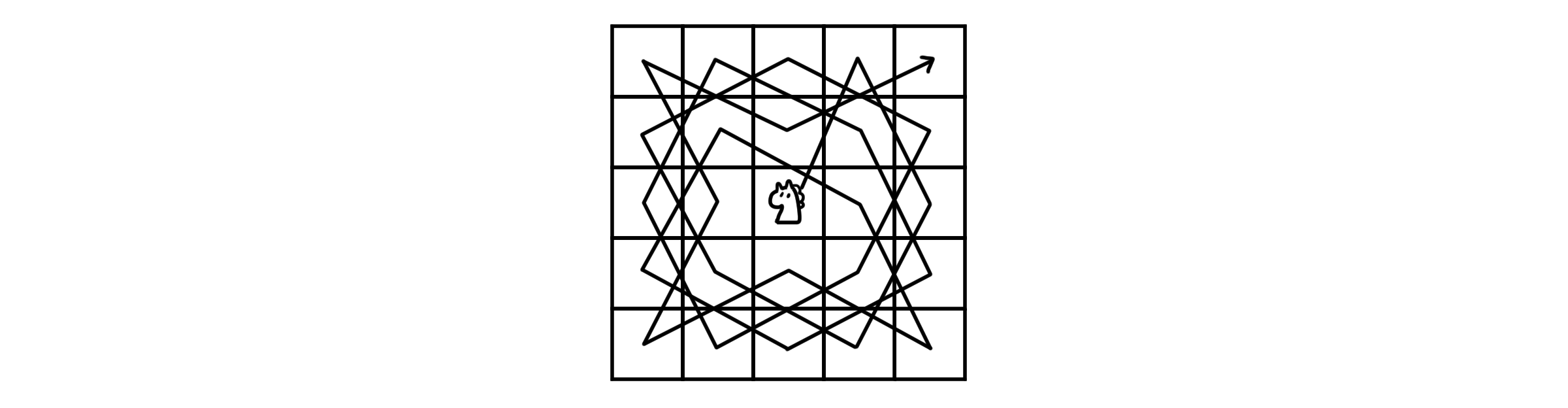
 나이트의 여행은 체스판에 오직 나이트 한 기 만이 있을 때, 나이트의 행마법을 이용해 체스판의 모든 칸을 한 번씩만 지나갈 수 있는지에 대한 문제입니다. 만약 모든 칸을 지나 시작점으로 다시 돌아올 수 있으면 그 여행은 닫혀있다고 말하고, 다른 점에서 순회를 끝낸다면 그 여행은 열려있다고 말합니다.

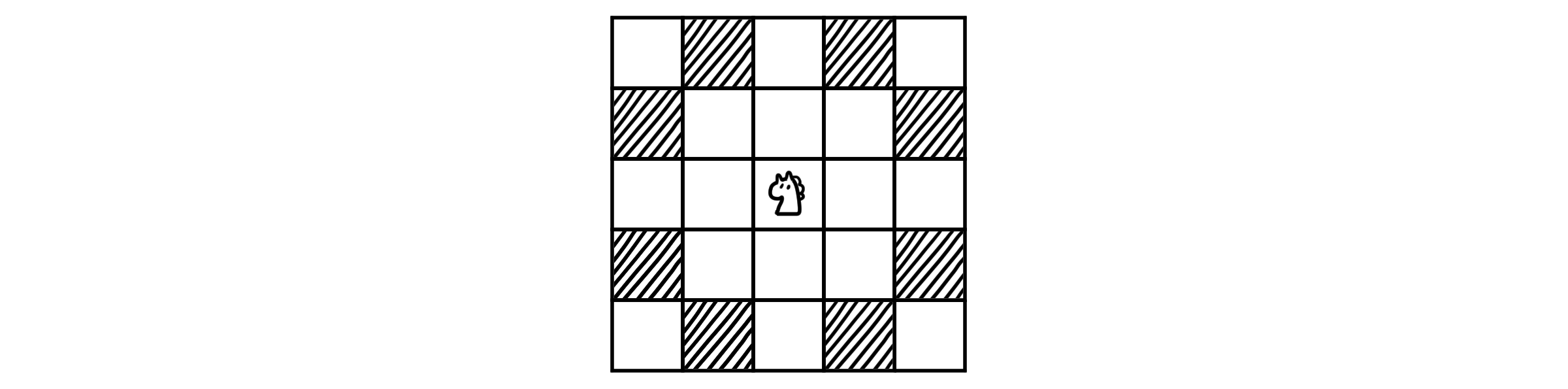
 모든 칸을 한 번씩만 지나간다는 점에서 알 수 있듯이 해밀턴 경로를 찾는 문제로 해석할 수 있습니다. 각 칸을 점으로, 다른 칸으로 갈 수 있는 경로를 선으로 두면 체스판 자체가 하나의 그래프가 되는 셈이죠. 예를 들어 5 * 5 크기의 체스판은 이런 그래프로 나타낼 수 있을 것입니다.

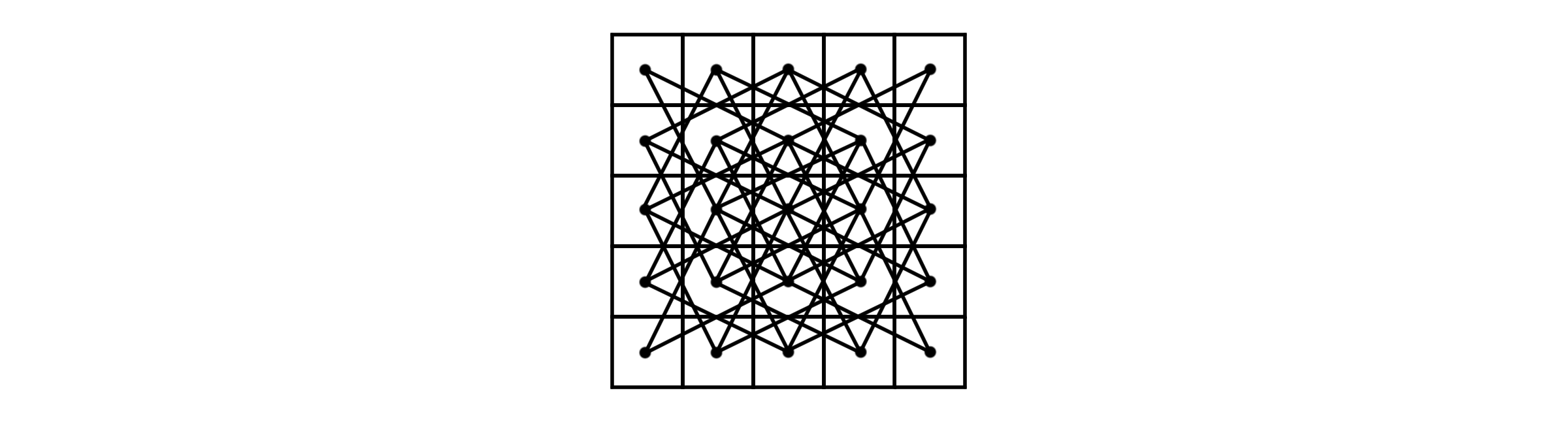
 이제 이 그래프에서 해밀턴 경로 또는 해밀턴 회로를 찾기만 하면 됩니다. 경로가 존재한다면 여행은 열려있을 것이고, 회로까지 있다면 여행은 닫혀있을 것입니다. 아래는 5 * 5 체스판에서의 열린 여행의 예시 중 하나입니다.

 참고로, 8 * 8 체스판에서는정확히 19,591,828,170,979,904개의 열린 여행과 26,534,728,821,064개의 닫힌 여행을 찾을 수 있습니다. 시간이 남으면 한 번 시도해보세요.

그레이 코드 (Gray code)

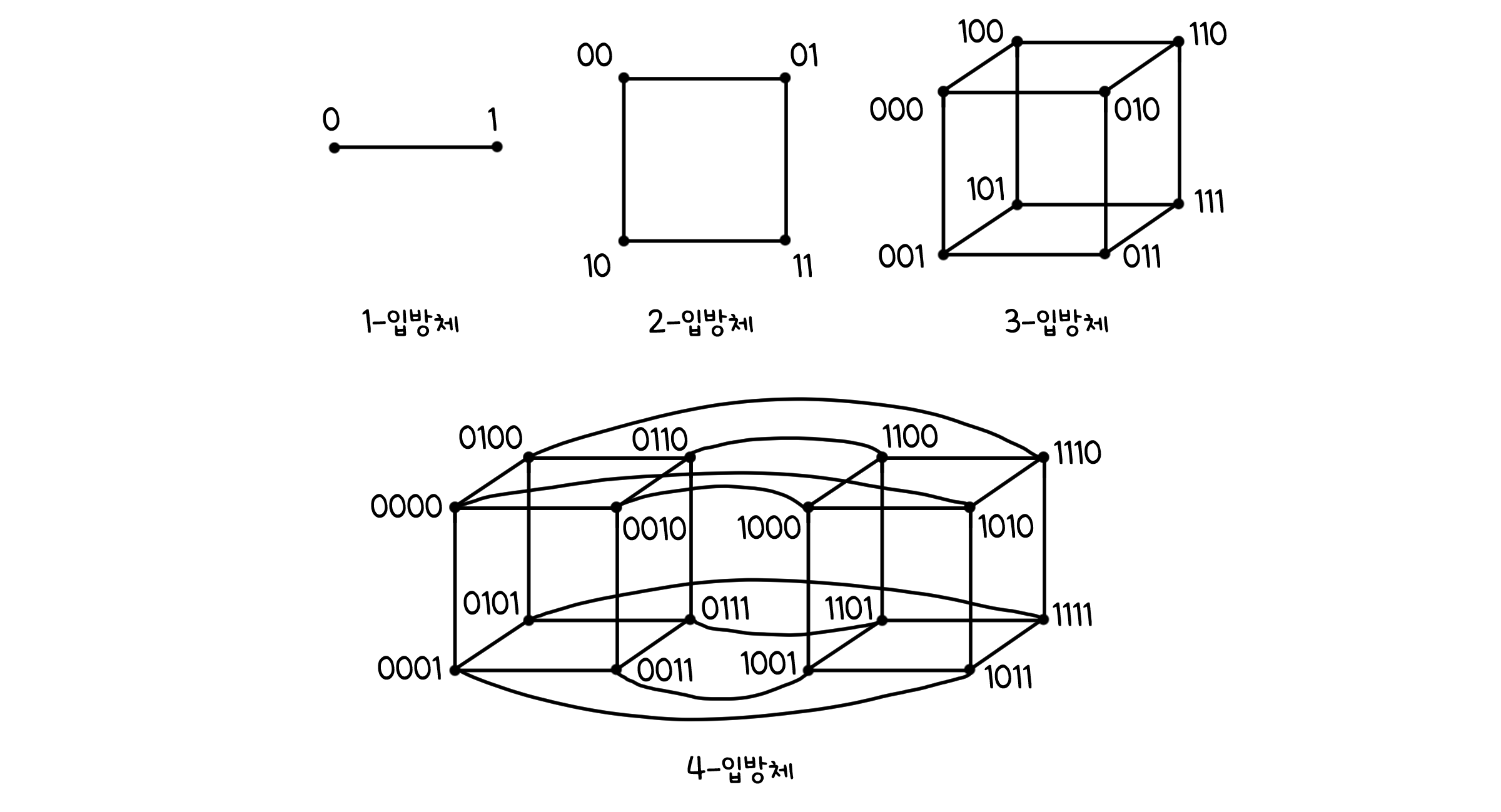
 그레이 코드란 서로 연속된 두 수가 한 비트만 다른 이진 코드입니다. 이진법과 비슷하지만 연산에는 쓰이지 않고, 주로 아날로그-디지털 변환이나 입출력 장치, 오류 정정 등에서 사용됩니다. 길이 n의 그레이 코드를 구하는 과정을 해밀턴 회로 그래프로 나타낼 수 있습니다. 그래프를 만드는 방법이 조금 특이한데, 다음을 만족하는 초입방체(Hypercube)를 사용할 것입니다.

• 각 점은 하나의 수를 가리킬 것

• 모든 점은 n개의 이웃을 가질 것

• 이웃 관계의 두 점은 하나의 비트만 다른 값을 가질 것

 이제 여기서 해밀턴 회로를 찾을 수 있다면, 해당 점들을 일렬로 나열함으로서 길이 n의 그레이 코드를 찾을 수 있게 됩니다.

순회 세일즈맨 문제 (Travelling salesman problem, TSP)

 여러분이 방문판매원이 되었다고 생각해봅시다. 도시의 각 지역을 돌아다니면서 영업을 해야 하고요. 한 지점에서 다른 지점으로 이동할 때 얼마나 시간이 걸리는지 알고 있다고 할 때, 최소 시간으로 모든 지역을 방문하는 경로를 찾는 문제가 순회 세일즈맨 문제입니다.

 각 지역은 점으로, 지역과 지역 사이를 선으로 생각한다면 이 역시 그래프로 나타낼 수 있습니다. 그렇게 되면 모든 점을 한 번씩만 방문해야 하니 해밀턴 경로를 찾는 문제가 됩니다. 하나 특별한 점이 있다면, 각 선마다 시간이라는 가중치가 존재한다는 것입니다. 단순히 경로를 찾는 것이 아니라, 경로를 찾으면서 시간이 최소가 되도록 신경써야한다는 뜻이죠.

순회 세일즈맨 문제를 빠른 시간 안에 풀 수 있는가는 아직 열려있는 문제입니다. 더 자세한 내용은 ‘알고리즘’에서 자세히 다루도록 하겠습니다.

다리 건너기 (재도전)

 오늘날 쾨니히스베르크에는 소련군의 폭격으로 두 개의 다리가 날아갔다고 하네요. 차수가 홀수인 점이 하나로 줄었으니, 이제 우리는 마음 놓고 오일러 회로를 순회할 수 있게 되었습니다.