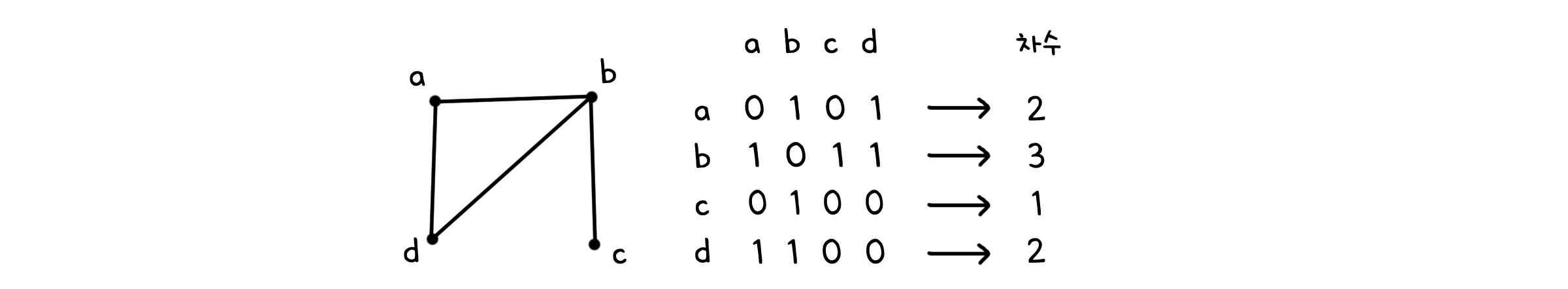[CM201] 07. 그래프 (Graph)

 여행을 떠나봅시다! 목적지를 정하고, 지도 앱의 네이게이션을 열면 길을 안내해 주겠죠?

 상황에 따라 다르겠지만, 대부분 여러 가지 경로를 보여줄거에요. 대중교통, 자동차, 자전거 등 수단에 따라 다를 수도 있고, 똑같이 차를 이용한다고 해도 시간이나 요금에 따라 다른 경로를 추천해주기도 합니다.

 길들은 블록이 많이 나뉘어진 도심지일수록 복잡해집니다. 교차로가 늘어나며 길의 가짓수도 늘어나고, 실시간 교통량에 따라 도로마다 걸리는 시간도 달라질 것입니다. 이런 환경에서 최적의 길을 찾기란 정말 까다로운 문제이죠.

 이제 길찾기를 위해 수학적 방법을 사용해 봅시다. 세상을 조금 단순하게 보는거에요. 가령… 그래프처럼 말입니다.

그래프 (Graph)

 그래프(Graph)는

 아니에요. 수학에서는 조금 다른 방식으로 정의됩니다. 그래프 $G$는 점(Vertex)들의 집합 $V$와 그 점들을 잇는 선(Edge)들의 집합 $E$의 묶음 $G=(V, E)$로 정의됩니다. 즉, 어떻게든 점들이 있고 그 점들이 이어져 있는 그림이면(심지어는 이어져 있지 않아도) 그래프라고 할 수 있습니다.

그래프의 선 (Edge)

 경우에 따라서 같은 두 점이 여러 개의 선을 가지는 경우도 있습니다. 이를 평행선(Parallel)이라고 합니다. 하나의 점이 혼자 선을 가지는 경우도 있는데, 이는 루프(Loop)라고 부릅니다.

 이 선들은 방향성을 가질 수도 있는데(이 경우 $e=(u, v)$와 $e’=(v, u)$는 서로 다른 선이 됩니다), 그 때 그래프는 방향이 있는 그래프 (Directed graph)라고 하며, 반대는 방향이 없는 그래프(Undirected graph)라고 합니다.

그래프의 점 (Vertex)

 그래프의 두 점 $u, v$가 선 $e$로 연결되어 있다면, 그 둘은 인접한다(Adjacent)고 합니다.

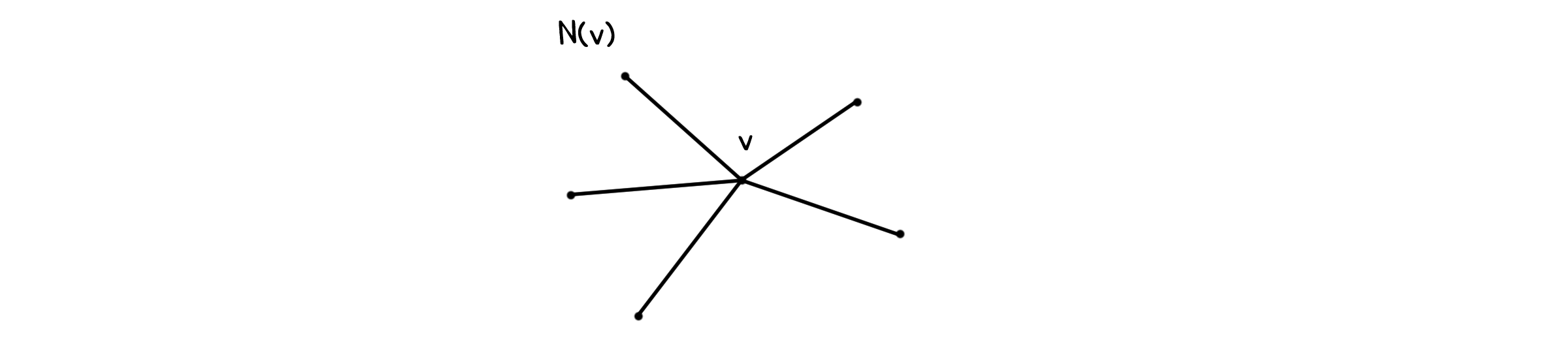
 그래프의 점 $v$에 대해 $v$와 인접한 모든 점들을 $v$의 이웃들(Neighborhood)이라고 하고, $N(v)$와 같이 표기합니다.

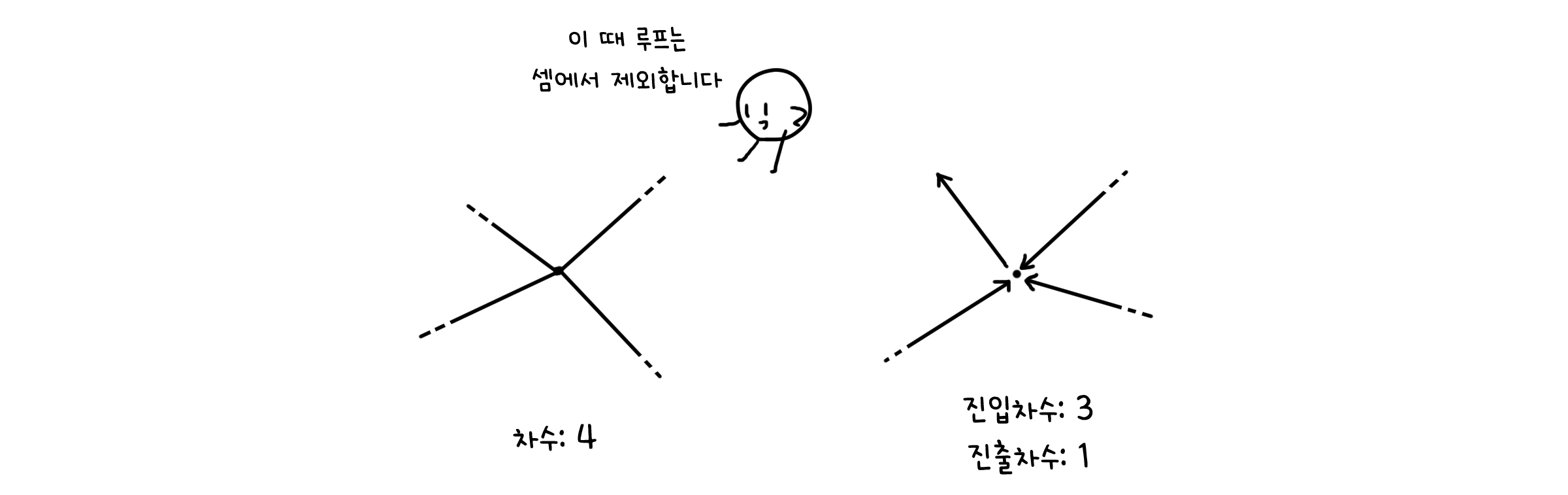
 그래프의 점 $v$에 대해 루프를 제외하고 $v$와 연결되는 선의 개수를 $v$의 차수(Degree)라고 합니다. 만약 방향이 있는 그래프라면, 선의 방향에 따라 점 $v$로 들어오는 방향의 선의 개수는 진입차수(In-degree, $deg^-(v)$), 나가는 방향의 선의 개수는 진출차수(Out-degree, $deg^+(v)$)라고 합니다.

Theorem 1. (Hanshaking 정리)
방향이 없는 그래프 $G=(V, E)$에 대해서 $E$의 크기가 $m$일 때, \(2m = \sum_{v \in V} deg(v)\)

Theorem 2.
방향이 없는 그래프에서 홀수 크기의 차수를 가진 점은 항상 짝수이다.

Theorem 3.
방향이 있는 그래프 $G=(V, E)$ 에서 \(|E| = \sum_{v \in V} deg^-(v) = \sum_{v \in V} deg^+(v)\)

그래프의 종류

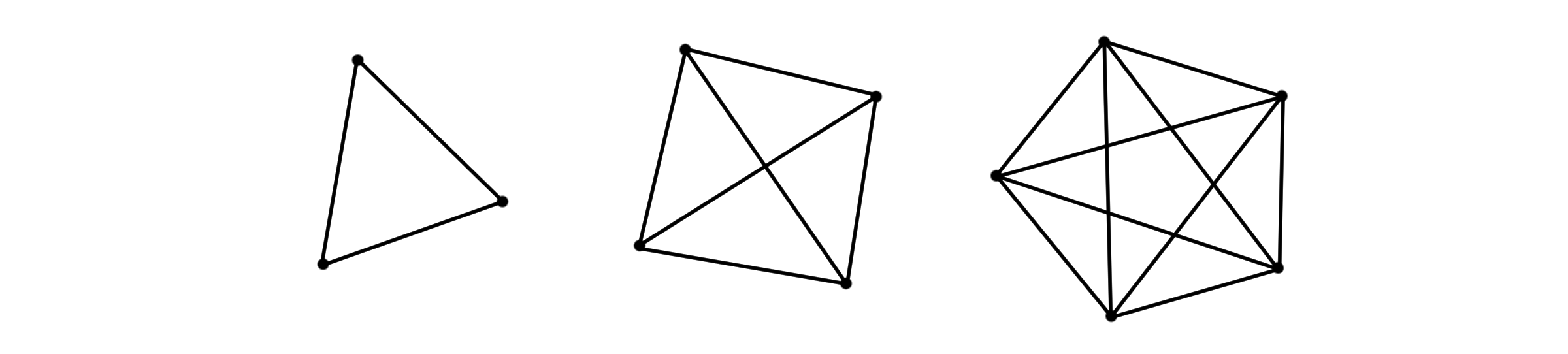
 그래프 $G=(V, E)$에서 모든 점 사이가 선으로 연결되어 있다면, 완전 그래프(Complete graph, $K_n$)라고 합니다.

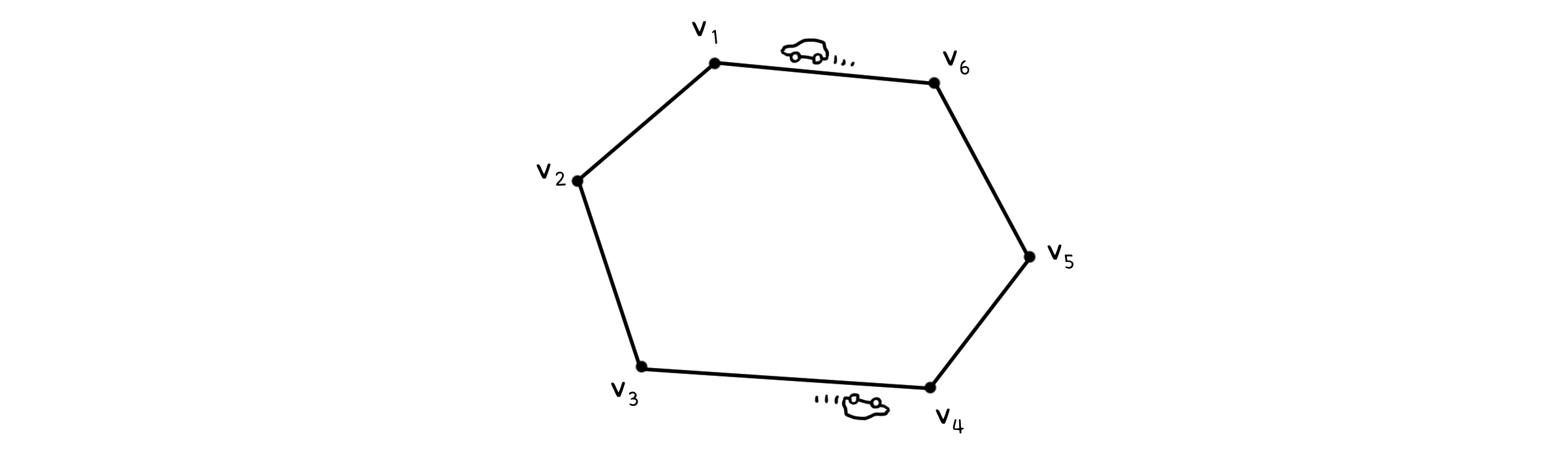
\[\forall u, v \in V \quad (u, v) \in E\]

 그래프 $G=(V, E)$에서 모든 점이 하나의 닫힌 고리로 연결되어 있다면, 사이클 그래프(Cycle graph, $C_n$)라고 합니다.

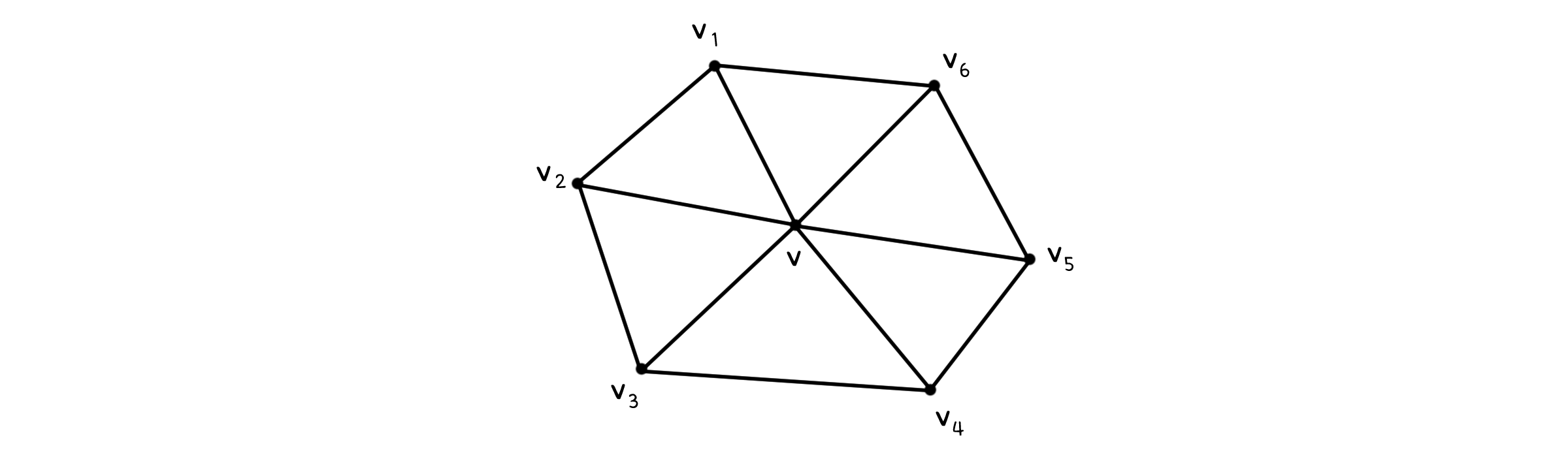
\[E = \{ (v_1, v_2), \; (v_2, v_3), \; … , \; (v_n, v_1) \}\]

 그래프 $G=(V, E)$가 사이클 그래프일 때, 다른 모든 점과 연결된 점 하나가 새로 추가되면 휠 그래프(Wheel graph, $W_n$)가 됩니다.

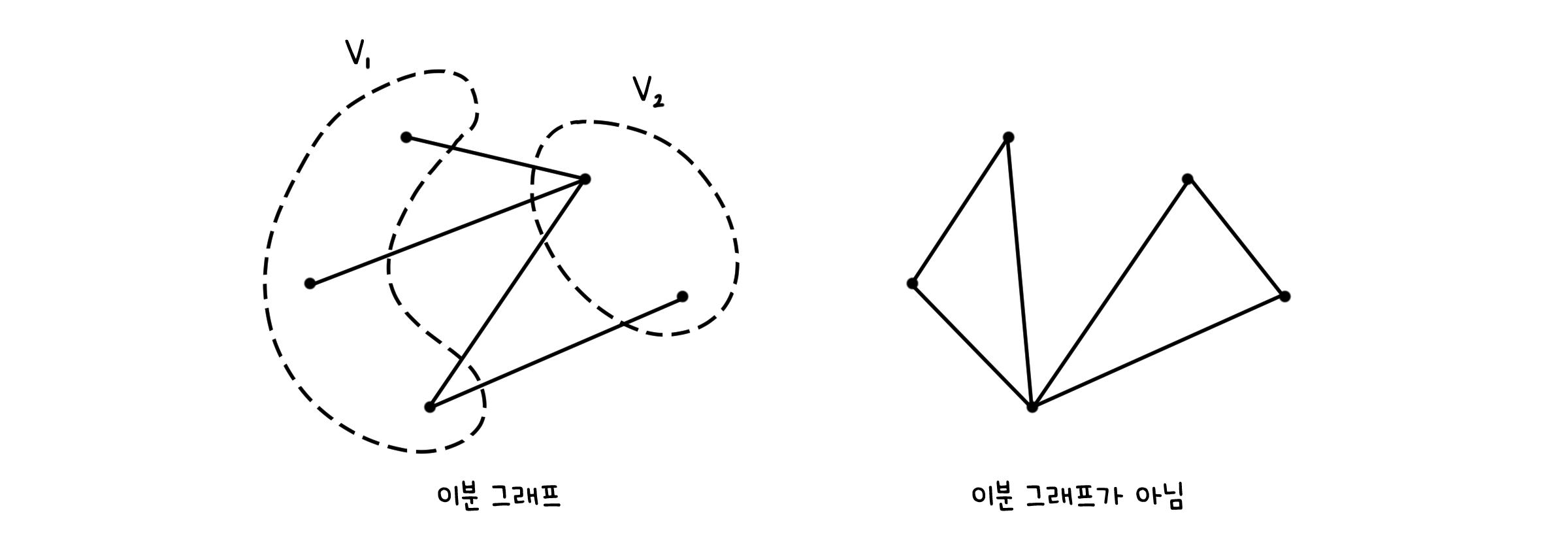
\[W_n = (V_c + \{v\}, E_c + \{ (v, v_1), \; …, \; (v, v_n) \})\]

 그래프 $G=(V, E)$가 모든 선 $e=(u, v)$에 대하여 $u \in V_1, v \in V_2$를 만족하게 하는 점의 하위 집합 $V_1, V_2$로 이등분 할 수 있으면, 이분 그래프(Bipartite graph)라고 합니다.

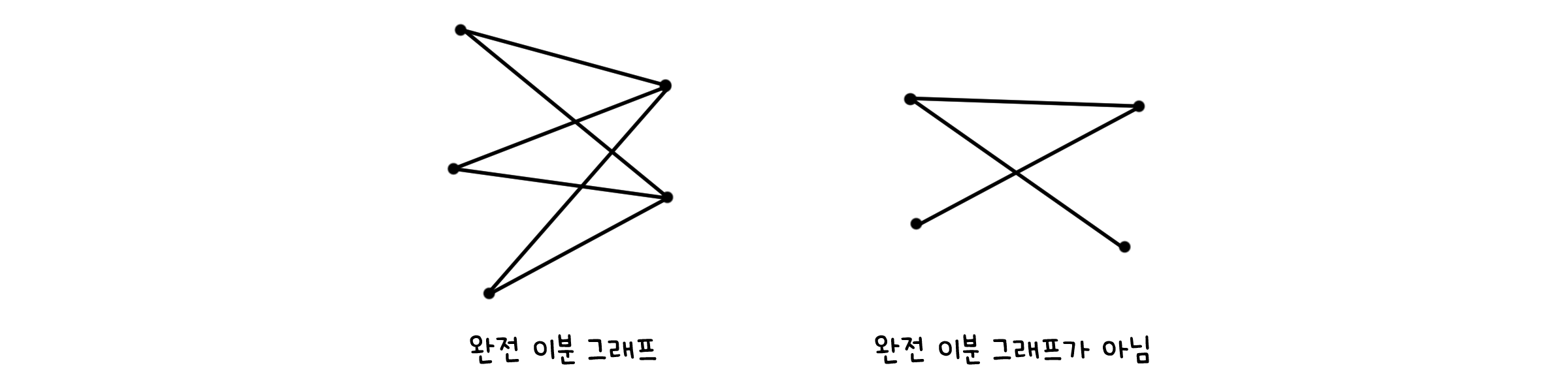
\[\exists V_1, V_2 \subset V \; s.t. \; V_1 \cap V_2 = \emptyset \; ∧ \; V_1 \cup V_2 = V\]

 이분 그래프 중에서도 조건을 만족하는 모든 선이 존재한다면 완전 이분 그래프(Complete bipartite graph, $K_{m,n}$)라고 부릅니다.

\[\forall v_1 \in V_1 \; v_2 \in V_2 \; \exists e=(v_1, v_2) \in E\]

그래프의 연산

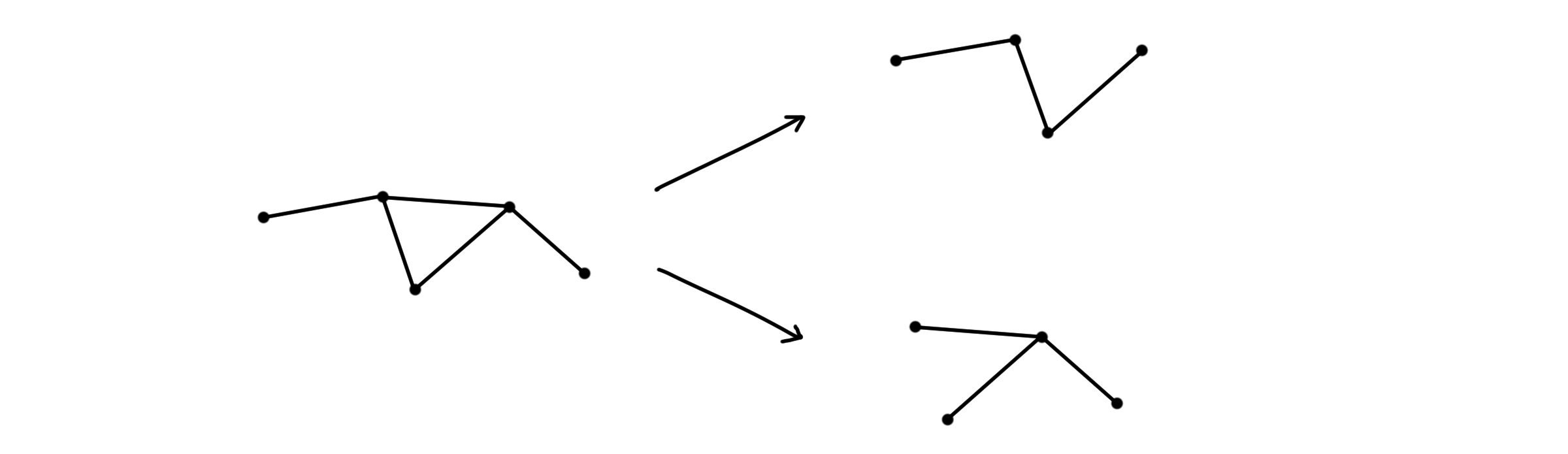
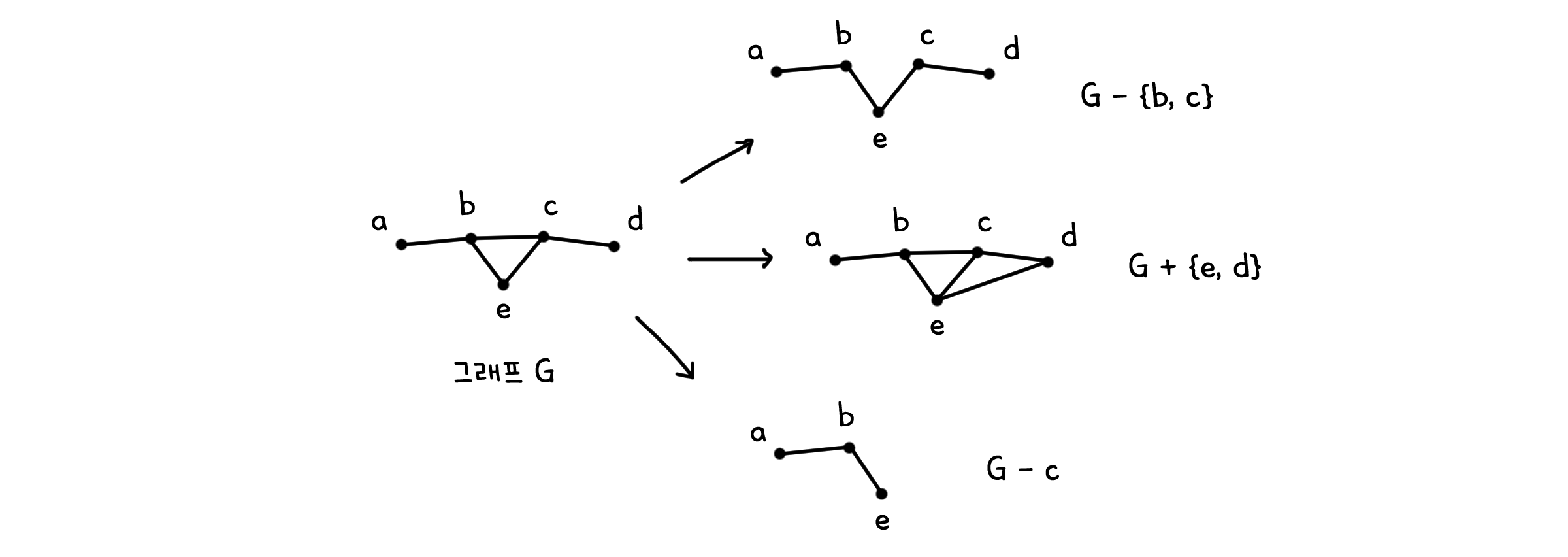
 보았듯이 그래프는 점과 선의 집합으로 정의되어 있습니다. 그 말은, 집합의 연산을 똑같이 적용해볼 수도 있다는 뜻입니다. 그래프의 부분집합이라고 볼 수 있는 하위 그래프(Sub graph)도 비슷하게 정의됩니다. 그래프 $G=(V, E)$가 있을 때 하위 그래프 $H$는 $V$와 $E$의 부분집합인 $W$와 $H$로 정의됩니다. 단, $F$의 점들이 모두 $W$에 속해야겠죠.

\[H = (W, F) \; s.t. \; (W \subseteq V) \; ∧ \; (F \subseteq E) ∧ (\forall f=(p, q) \in F, \quad p, q \in W)\]

 같은 맥락으로 집합의 연산처럼 그래프에서도 다른 그래프를 더하거나 뺄 수 있습니다.

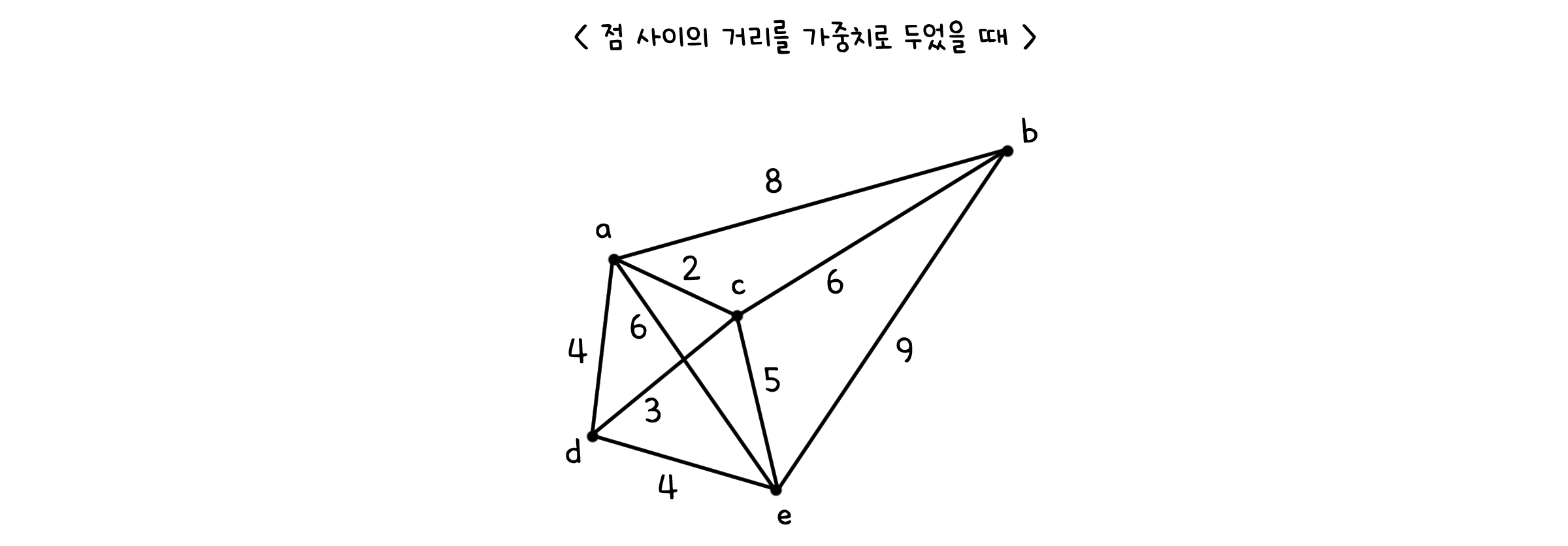
가중치 그래프 (Weighted graph)

 그래프의 모든 선이 항상 똑같은 가치를 가지지는 않습니다. 당장 겉보기만 해도 길이부터가 다르니까요.

 비록 이런 특징을 점과 선의 집합에서 나타낼 수는 없지만, 각 선에 대응하는 가중치 함수를 따로 둠으로서 반영할 수는 있습니다.

그래프의 표현법

인접 행렬 (Adjacency matrix)

 그래프를 나타내는 데에는 그림이나 집합 말고도 다른 방법이 있습니다. 결국 그래프도 관계(Relation)의 일종이기 때문에, 선에 포함된 점들이 관계에 속해 있다고 생각한다면 이를 행렬로 표기할 수 있는 것이죠. 이를 인접 행렬(Adjacency matrix)라고 합니다. 선 $e=(u, v)$가 있을 때, 인접 행렬 $A$의 성분 $a_{u, v}$의 값은 1이 됩니다(없다면 0 이겠죠). 만약 평행선을 가진 그래프라면, 행렬 성분의 값은 선이 있는지 없는지가 아닌, 몇 개의 선을 가지고 있는지가 될 것입니다.

 그래프를 행렬로 나타내면 몇 가지 연산을 간편하게 할 수 있습니다. 가령 어떤 점 $v$의 차수를 알고 싶다면, $v$에 해당하는 열 또는 행의 값들에서 대각성분(이는 루프에 해당합니다)을 제외하고 모두 더하기만 하면 됩니다.

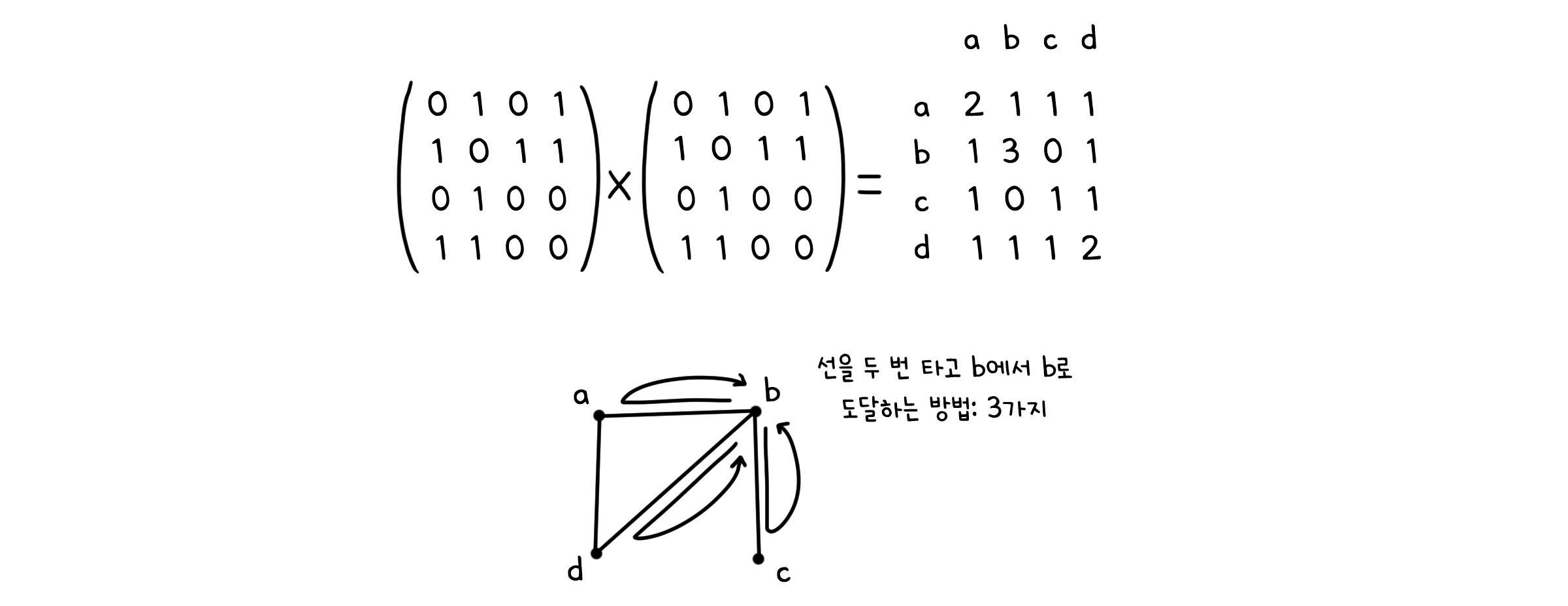
 또한 행렬을 거듭제곱 곱셈한다면, 해당 그래프에서 선들을 이어 도달할 수 있는 경로에 대해 알 수 있습니다. 이는 5장에서 관계의 추이성(Transitivity)을 확인할 때도 언급한 내용인데, 앞서 언급했듯이 그래프 또한 관계의 일종으로 볼 수 있기 때문에 일맥상통한다고 볼 수 있습니다. 인접 행렬 $A$는 선을 타고 한 번 이동해서 이동해서 도달할 수 있는 점, $A$의 제곱 $A^2$은 선을 타고 두 번 이동해서 도달할 수 있는 점을 나타내게 됩니다.

Theorem 4.
인접 행렬 $A$에 대해 $A^n$의 ij 번째 성분은 길이 점 i에서 점 j로 도달하는 길이 n 만큼의 경로의 개수이다.

동형사상 (Isomorphism)

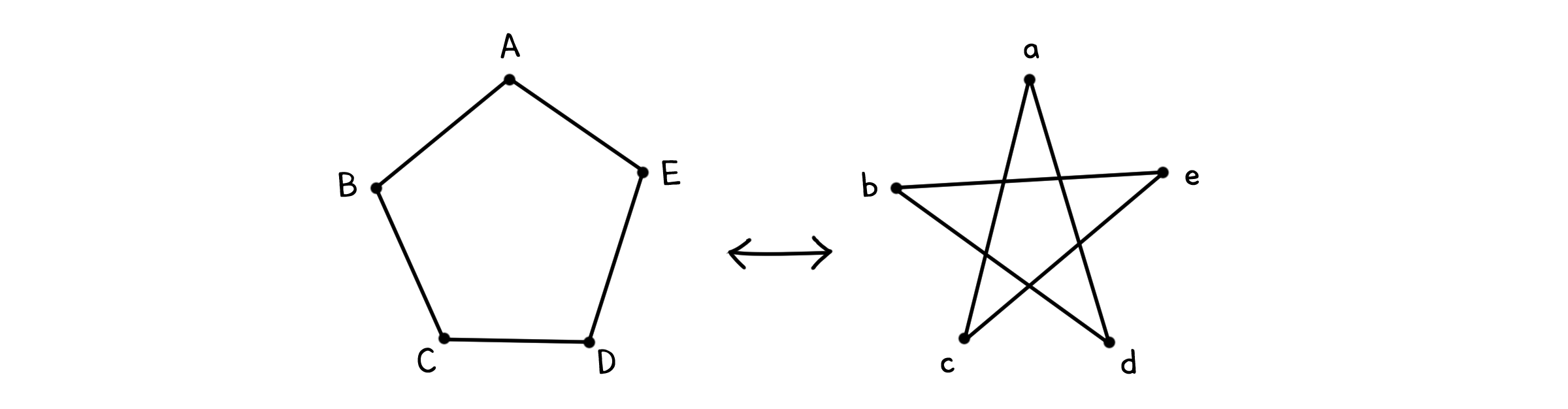
 이론상 동일한 인접행렬을 가지고 있다면 두 그래프는 동일하다고 볼 수 있습니다. 하지만 똑같은 그래프라고 해도, 실제로 그릴 때는 다른 형태로 그릴 수도 있죠. 마치 머그잔과 도넛이 위상적으로는 같지만, 생긴게 다른 것 같다고나 할까요.

 이렇게 두 그래프가 정의된 구조가 서로 동일하다면, 둘은 동형사상(Isomorphism)이라고 합니다. 좀 더 수식적으로, 엄밀하게 정의한다면 두 그래프 $G_1 = (V_1, E_1)$, $G_2 = (V_2, E_2)$가 있을 때 각각의 점과 선들이 대응되는 일대일 함수 $f: V_1 \rightarrow V_2$ 와 $g: E_1 \rightarrow E_2$ 가 다음을 만족할 때 동형사상이라고 말할 수 있습니다.

\[e=(w, v) \in E_1 \; \leftrightarrow \; g(e)=(f(v), f(w)) \in E_2\]

Theorem 5.
그래프 $G_1$와 $G_2$의 인접 행렬이 동일하다면, 두 그래프는 동형사상이다.

 두 그래프가 서로 동형사상인지 파악할 때 무작정 모양을 바꿔가며 확인하는 것은 상당히 까다로운 일입니다. 점이 $n$개 있다고 하면 서로의 점들을 대응시키는 방법은 $n!$개나 되니까요. 어쩔 때는 두 그래프가 동형사상이 아니다는 것을 증명하는게 더 빠를 때도 있습니다. 점 또는 선의 개수가 다르거나, 차수가 다른지 확인하기만 해도 이들이 동형사상이 아닌지 확인할 수 있습니다.

 이 때까지 그래프에 대한 정의와 그 표현법에 대해서 살펴 보았는데, 경로와 길을 찾는 방법에 대해서는 다음 장에서 본격적으로 다루도록 하겠습니다.