[CM201] 06. 추론 (Inference)

이때까지 다루었던 내용들을 써 먹어 볼 시간입니다. 여러 가지 문제들을 해결하는데 도움이 되는 기본적인 추론 과정들에 대해 소개하겠습니다.

귀납법과 연역법 (Induction & Deduction)

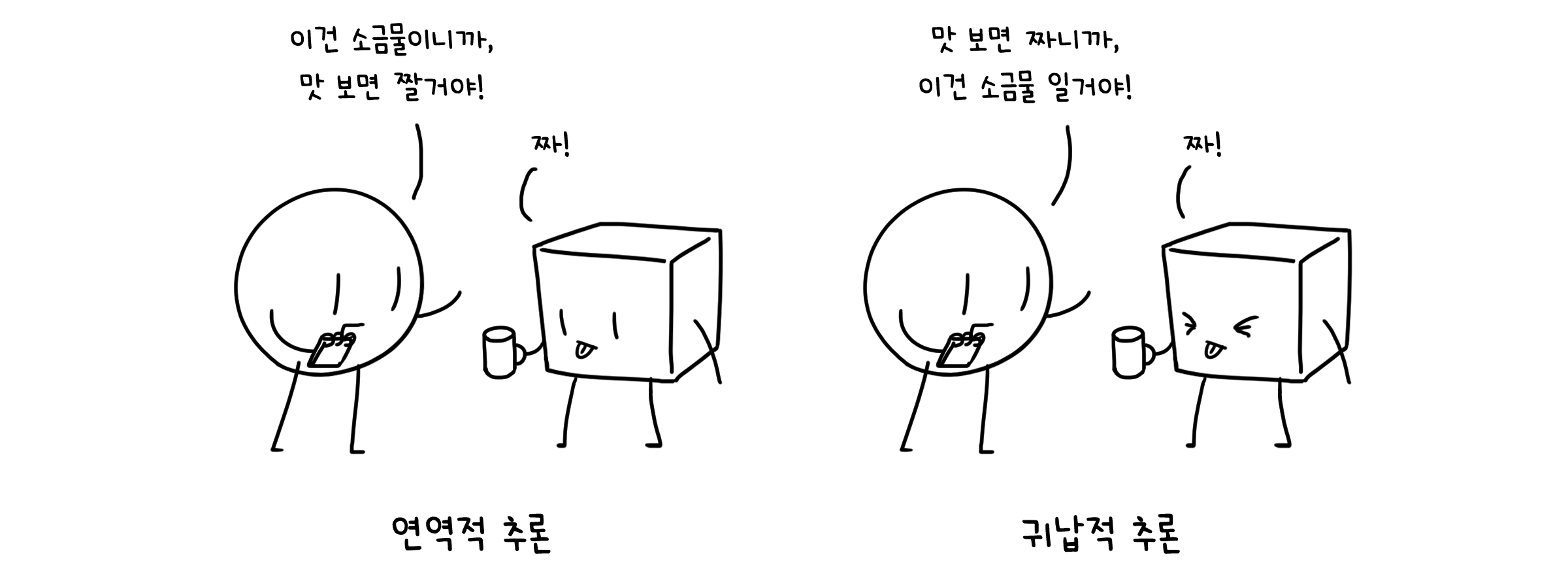
 어떤 문제를 해결하는데 사용하는 추론 방법은 크게 연역적인 경우와 귀납적인 경우로 구분할 수 있습니다. 연역(deduction)은 일반적 원리에서 개별적 결론을 이끌어내는 추론 방식이고, 귀납(induction)은 개별적 사례들에서 일반적 원리를 발견하는 추론 방식입니다.

 귀납적 사고방식은 주로 과학적인 사실을 밝혀내는데 사용됩니다. 세상에 벌어지는 다양한 현상들을 관찰하고 수집하여, 거기서 보이는 어떤 공통적인 패턴을 찾아 법칙이라는 이름을 붙이는 것이죠. 결론은 어디까지나 맞는게 아닌, 가능성이 높은 편일 뿐입니다. 새로운 반례가 나타나면 깨질 수도 있죠. 과학계가 매번 뒤집히고 들썩이고 하는 이유가 이 때문이에요.

 반면 이때까지 논리를 다루는 방법을 보면 알 수 있듯이, 수학은 귀납적 추론을 허용하지 않습니다. n이 1일 때, 2일 때, 3일 때… 등 자잘한 사례들을 모아 명제를 증명해도, 그게 모든 자연수 n에 대해서 성립한다고 말할 수는 없으니까요. 대신 정의와 정리라는 일반적인 원리를 기반으로 증명을 통해 새로운 정리를 이끌어내는 연역적 사고방식을 사용하게 됩니다.

수학적 귀납법 (Mathematical induction)

 그래서, 우리가 알아볼 것은 수학적 귀납법입니다.

 네. 이건 수학적 귀납법입니다. 사실 이것도 연역적 추론 방식의 일부입니다. 우선, 수학적 귀납법을 수식으로 나타내면 이렇게 요약할 수 있습니다.

\[\forall n \in \mathbb{Z}^+, \quad \{S(1) ∧ (\forall n \; S(n) \rightarrow S(n+1))\} \; \rightarrow \; \forall n \; S(n)\]

 상당히 복잡해 보이지만, 하나씩 뜯어봅시다…

 $S(n)$은 명제함수입니다. $n$에 어떤 값이 들어오느냐에 따라 참 또는 거짓이 결정됩니다. 맨 앞의 양화사는 여기서 $n$이 양의 정수, 그러니까 $n=1, 2, 3,…$의 범위에 있다는 것을 말해줍니다. 그러면 위 식의 결론 $\forall n \; S(n)$는, 모든 n에 대하여 $S(n)$을 만족한다고 생각할 수 있겠네요. 수학적 귀납법을 통해 증명하려고 하는 내용이죠.

 이제 이 결론을 만족하기 위한 조건을 두 개로 나눌 수 있습니다.

• 기본 단계 (Base step) : $S(1)$

• 귀납적 단계 (Inductive Step) : $\forall n \; S(n) \rightarrow S(n+1)$

 기본 단계는 $n=1$일 때, 즉 제일 처음의 경우에 대해 $S(n)$이 참이어야 한다는 조건입니다. 그리고 귀납적 단계는 모든 n에 대해 $S(n)$이 참일 경우 $S(n+1)$ 또한 참이어야 한다는조건입니다. 그러니까 이렇게 다시 적을 수 있겠네요.

• 기본 단계 (Base step) : $n=1$일 때 참이다.

• 귀납적 단계 (Inductive Step) : $n=k$일 때 참이면, $n=k+1$일때도 참이다.

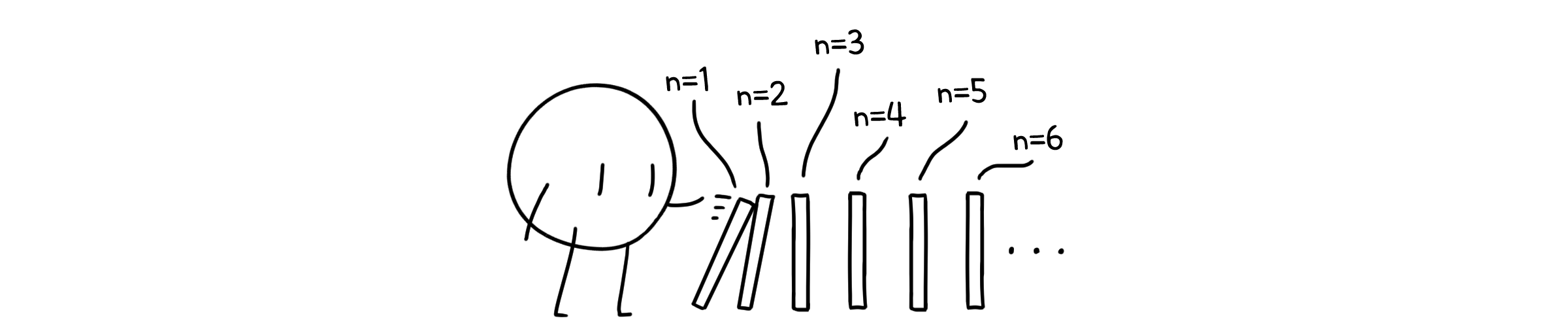
 한 경우가 참일 때 그 다음 경우도 참이 된다는 사실이 밝혀지면, 제일 첫 경우가 참이기만 해도 다른 경우들이 꼬리에 꼬리를 물고 참임이 밝혀지게 됩니다. 그렇게 이론적으로 모든 $n$에 대해 명제가 참이 됨을 보일 수 있습니다.

수학적 귀납법 - 증명

 조금 더 엄밀하게 이 방법이 문제 없다는 것을 증명해볼게요. 귀류법을 사용하겠습니다.

 만약 위의 방법을 사용해 증명 했음에도, 기어코 $S(n)$이 거짓이 되는 n들을 찾아버렸다고 가정해봅시다. 이를 모아 집합 $P$라고 하고요.

\[P = \{n | S(n) = \text{false}\}\]

 $P$ 안에는 필시 최솟값을 가지는 $n$값 $k$가 있을 것입니다. 이 $k$값도 두 가지 경우가 있을 거에요.

• $k = 1$ 일 때

• $k > 1$ 일 때

 이 두 가지 경우에 대해 각각 모순이 발생함을 보여주면 됩니다.

• $k = 1$ 일 때 : 이미 수학적 귀납법을 통해 $n = 1$ 일 때 $S(n)$이 참임을 보였어요. 바로 모순입니다.

• $k > 1$ 일 때 : $k$가 $n$ 중에서 최솟값이 아니기 때문에, 반드시 $k$보다 1 작은 $k-1$이 $n$중에 있을 것입니다. 그리고 $k$는 $P$ 중에서 최솟값이므로, $n = k-1$ 일 때 $S(n)$은 거짓이 아니겠고요. 그러면 참이란 말인데, 우리는 이미 수학적 귀납법을 통해 $S(n)$이 참일 때 $S(n+1)$도 참임을 보였어요. 즉 S(k-1)이 참이니 S(k) 또한 참이라는 뜻이죠. 하지만 우리는 n=k일 때 $S(n)$이 거짓이라는 가정을 했었으니, 모순이 됩니다.

 모든 경우에 대해 $P$의 최솟값인 $k$의 존재가 부정당했으므로, $P$는 존재할 수 없습니다. 따라서 귀납법을 통해 모든 $n$에 대해 $S(n)$이 참이 됨을 증명할 수 있게 됩니다! $\Box$

 이 모든 증명 과정은 $n$이 속한 자연수가 잘-정렬된 집합(Well-ordered set)이기 때문입니다. 반드시 최솟값이 존재하고, 이를 시작으로 순서를 세울 수 있는 집합인 것이죠.

좀 더 강한 조건을 가진 수학적 귀납법도 있습니다. 이 때는 $S(n-1)$이 참이면 $S(n)$도 참이 아닌, $S(1)$ 부터 $S(n-1)$까지 모두 참이면 $S(n)$도 참이어야 합니다. 즉, \(\quad \forall k \; (1 \leq k < n) \quad S(k) \rightarrow S(n)\)

수학적 귀납법 - 예시

 수학적 귀납법을 통해 참임을 밝힐 수 있는 간단한 명제를 살펴봅시다.

모든 자연수 $n$에 대해 $5^n - 1$은 4로 나누어 떨어진다.

• $n = 1$ 일 때 : $5 - 1 = 4$ 니까 당연히 4로 나누어 떨어집니다. → 참!

• $n = k$ 일 때 : $5^k - 1$가 4로 나누어 떨어진다고 가정합시다. 그러면 $5^k - 1 = 4m \; (m \in \mathbb{Z}^+)$라고 둘 수 있습니다. 그러면 $5^k = 4m + 1$로 나타낼 수 도 있습니다.

• $n = k+1$ 일 때 : $5^{k+1} - 1 = 5 * (4m + 1) - 1 = 4 * (5m + 1)$. 즉, 4로 나누어 떨어질 수 있습니다. → 참!

 따라서, 모든 자연수 $n$에 대해 $5^n - 1$은 4로 나누어 떨어진다는 명제는 참입니다. $\Box$

문자, 문자열, 문자열들..

 순서구조(Sequence)는 정의역이 연속적인 정수로 정의된 특별한 형태의 함수 입니다. 좀 더 쉽게 말하면, 순서 번호(인덱스)를 매길 수 있는 값들의 나열이라고 볼 수 있겠습니다.

 그 중에서 문자열(String)은 특히, 그 값이 문자로 이루어져 있는 경우입니다. 순서가 있기 때문에, 문자들의 순서가 뒤바뀌거나 같은 문자가 중복되어 나타나도 다른 문자열로 볼 수 있습니다. 문자열과 관련된 대표적인 연산으로는 그 길이(Length)를 구하거나 뒤집고(Reversal), 두 문자열을 합치거나(Concatenate) 하위 문자열(Substring)을 구하는 것 등이 있습니다.

 갑자기 왜 문자열 이야기를 하냐고요? 이런 문자열 연산들을 간단히 표현할 수 있는 방법에 대해 소개하려고요. 바로 재귀입니다.

재귀 (Recursion)

 재귀(Recursion)은 문제를 자기 자신보다 더 작은 문제로 정의하는 방법입니다. 그 새로운 문제가 원래 문제와 유사한 형태를 띠기 때문에, 자기 자신으로 돌아온다는 의미를 가지게 되었습니다.

 재귀적 표현은 크게 두 부분으로 이루어져 있습니다. 더 이상 분해할 수 없는 최소 단위에 대한 정의인 기본 단계(Basis step)와 더 작은 문제로 분할할 수 있어 재귀 표현이 가능한 재귀 단계(Recursive step)가 있죠. 앞서 정의했던 문자열과 문자열의 연산들을 재귀적 표현으로 나타내면 아래와 같습니다.

	기본 단계	재귀 단계
문자열 정의($w$)	$w=\lambda$	$w = w’x$
문자열 길이($L(w)$)	$L(\lambda) = 0$	$L(wx) = L(w) + 1$
문자열 결합($C(a, b)$)	$C(a, \lambda) = a$	$C(a, xb) = C(ax, b)$
문자열 반전($R(w)$)	$R(\lambda) = \lambda$	$R(wx) = xR(w)$

($\lambda$ : 빈 문자열, $x$ : 문자)

재귀를 이용해 문제를 표기하는 방법을 회귀(Recurrence)라고 합니다. 회귀를 이용해 문제를 해결하는 대표적인 방법으로 분할 정복(Divide and conquer)이 있는데, 이에 대해서는 ‘알고리즘’에서 자세히 다루도록 하겠습니다.