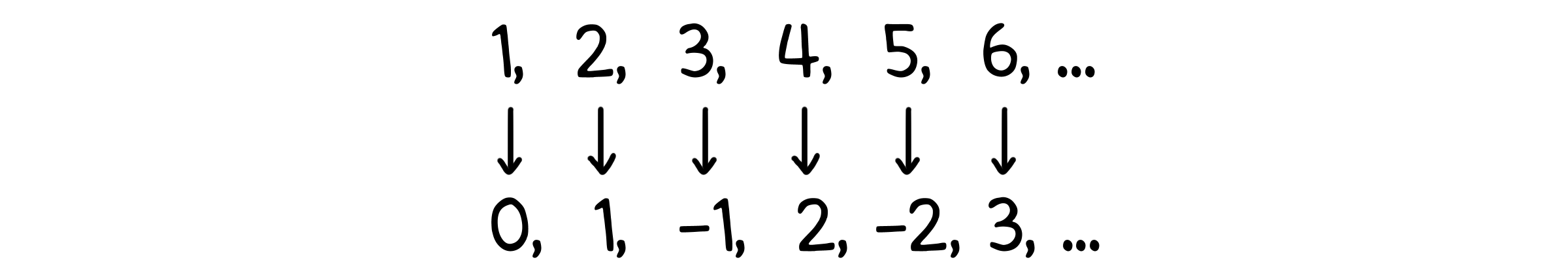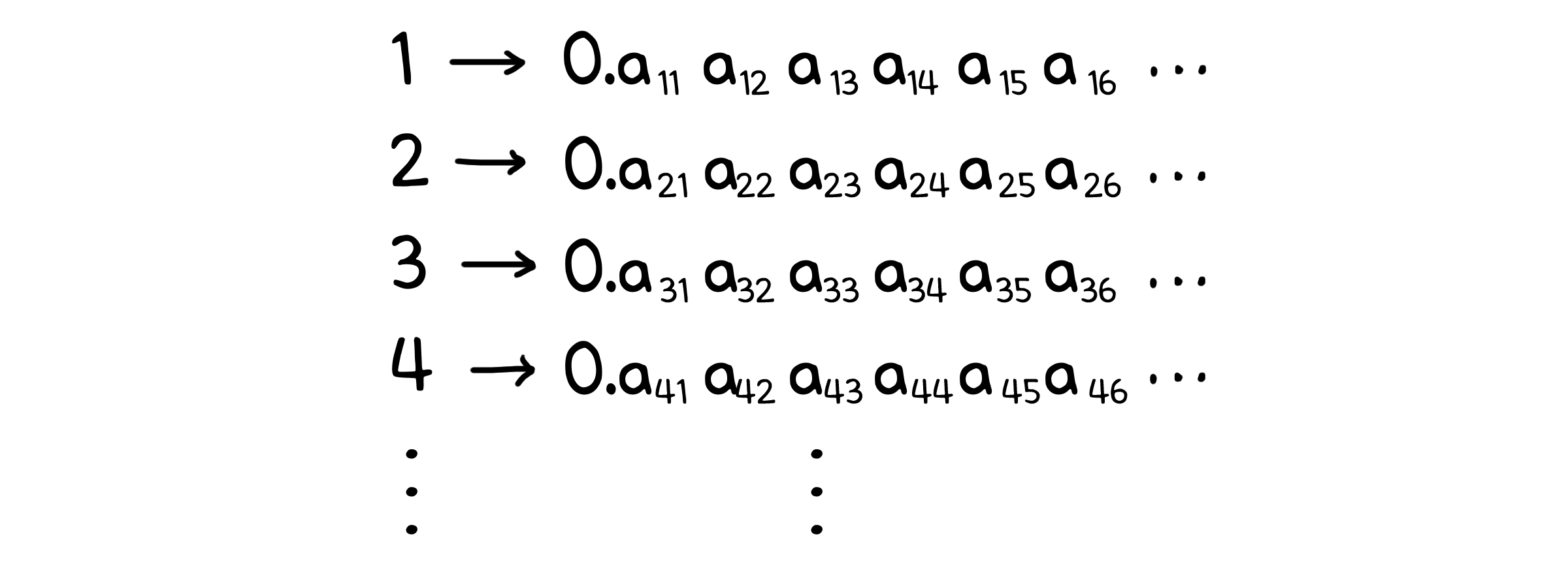[CM201] 04. 집합(Set)

집합(Set)

 이전까지는 논리를 통해 참과 거짓을 다루었다면, 이제부터는 그 논리가 가리키는 요소들을 어떻게 모으는지에 대해 다뤄보려고 합니다. 그리고 그 중심에 있는 개념이 바로 집합(Set)입니다.

 우리는 살면저 정말 많은 종류의 사람들을 만날 수 있습니다. 그리고 어쩌다가 그런 사람들이 무리지어 있는 공동체를 발견할 수도 있죠. 학교라던가, 학교라던가, 학교 같은 곳이요. 이곳의 사람들은 각양각색으로 보이지만, 여러분은 이들을 비슷한 부류들로 나눌 수 있음을 깨닫게 됩니다. 학부생과 교직원, 새내기와 헌내기, 남학생과 여학생 등 여러가지 기준으로 구성원이 분류됩니다.

 이렇게 서로 다른 요소들이 순서 없이 모여 있는 형태를 집합이라고 합니다. 집합 안에 있는 요소들을 원소(Element)라고 하며, 집합안에 있는 원소의 개수를 집합의 크기(Cardinality)라고 합니다. 집합은 그 요소들을 중괄호{ }로 묶어 표현합니다.

집합의 종류

 아무런 원소도 가지지 않은 집합을 공집합(Empty set)이라고 합니다.

\[A = \emptyset\]

 한 집합 A의 원소들을 다른 집합 B가 모두 가지고 있다면 A는 B의 부분집합(Subset)이라고 합니다.

\[A = \{1, 2, 3\}, \; B = \{1,2, 3, 4, 5\} \; \rightarrow A \subset B\]

 멱집합(Power set)은 한 집합의 모든 부분집합을 원소로 가지고 있는 집합입니다.

\[A = \{1, 2, 3\} \; \rightarrow P(A) = \{\{\emptyset\}, \{1\}, \{2\}, \{3\}, \{1, 2\}, \{1, 3\}, \{2, 3\}, \{1, 2, 3\}\}\]

 한 집합의 원소들을 서로 겹치지 않게 나눠 가진 부분집합들의 모임을 그 집합의 분할(Partition)이라고 합니다. 때문이 분할들의 교집합은 항상 공집합이며, 합집합은 원래 집합이 됩니다.

\[A = \{1, 2, 3\}, B = \{1\}, C = \{2, 3\} \; \rightarrow \text{B와 C는 A의 분할}\]

 만약 A와 B의 원소들이 모두 일치한다면, 두 집합은 같은 집합이라고 할 수 있습니다.

\[A = \{1, 2, 3\}, B = \{1, 2, 3\} \; \rightarrow A = B\]

집합의 연산

 우리가 명제에서 논리 연산을 한 것과 같이, 집합도 비슷한 연산을 할 수 있습니다. 다른 점이 있다면 차집합에 대한 연산이 따로 존재한다는 것입니다.

단어	연산	연산자
A가 아니다	여집합 (Complement)	$\bar{A}$
A 이고 B	교집합 (Intersection)	$A ∩ B$
A 이거나 B	합집합 (Union)	$A ∪ B$
B가 아닌 A	차집합 (Difference)	$A - B$

 카르티시안 곱(Cartesian Product)은 두 집합의 특이한 곱 연산입니다. 이전에 02.논리 (Logic)에서 이야기했던 양화사 같이쓰기에 대해 떠올려봅시다.

\[\neg \; \forall x \; \exists y P(x, y)\] \[\neg \; \exists x \; \forall y P(x, y)\]

 이 경우는 변수가 $x$, $y$ 두 가지였죠. 두 변수는 각각의 범위가 있을 것입니다. $x$, $y$가 될 수 있는 범위를 나타낸 집합을 $X$, $Y$라고 했을 때, $P(x, y)$가 참인지 확인하기 위해서 우리는 $X$에서 원소를 하나, $Y$에서 원소를 하나 뽑아 짝지은 경우들을 하나하나씩 고려해야 합니다. 순서쌍으로 나타내면 $(x, y)$가 되겠네요. 이 순서쌍을 원소로 하여 만들어지는 집합이 바로 카르티시안 곱, $X \times Y$입니다.

 순서쌍이라고 한 만큼, 이 집합의 원소들은 모두 순서를 가지고 있습니다. 즉, $(a, b)$와 $(b, a)$가 서로 다른 원소로 취급된다는 뜻입니다.

집합의 크기

 집합의 크기는 원소의 개수로 나타낸다고 했습니다. 이 개수를 기준으로 집합을 구분할 수도 있습니다. 간단히 원소가 유한하면 유한집합(Finite set), 무한하면 무한집합(Infinite set)으로요.

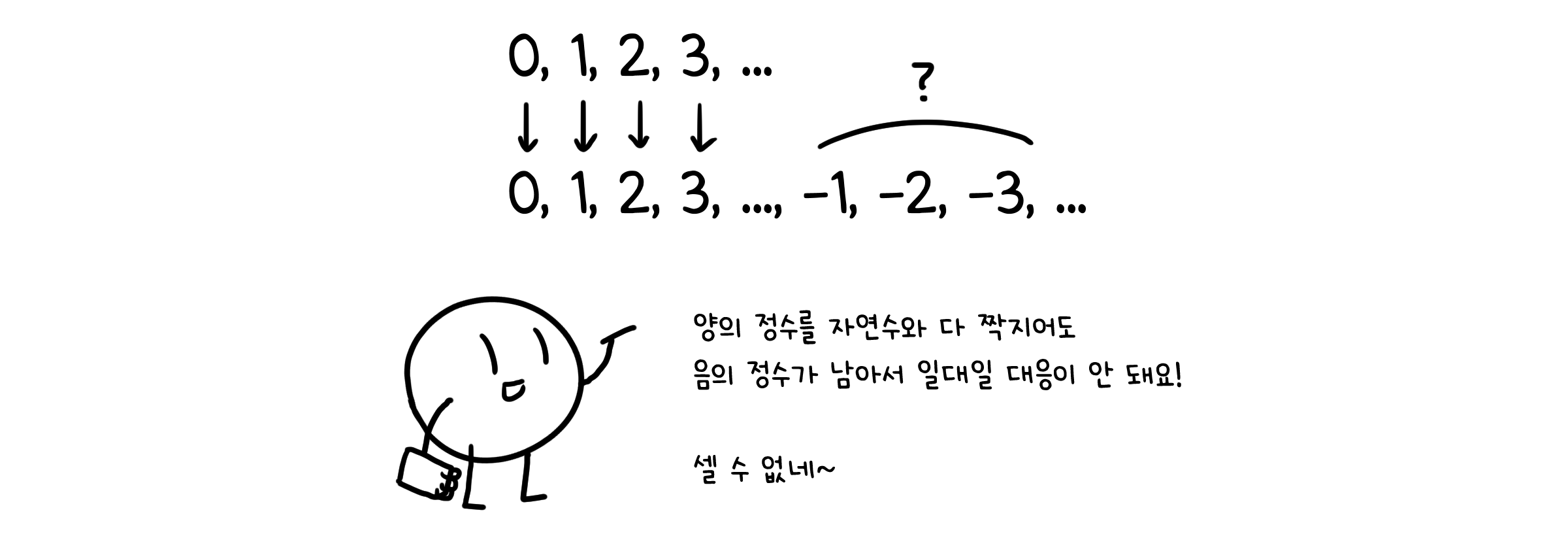
 유한집합은 별로 문제가 되지 않습니다. 열심히 하나씩 센다면 우리는 집합 안의 원소 개수를 정확하게 알 수 있을테니까요. 그런데 무한집합은…? 어차피 무한하니까 셀 필요가 없는걸까요? 그렇다면 정수의 집합과 실수의 집합은 그 크기가 똑같다고 해야 하나요? 그래도 실수가 훨씬 많을 것 같지 않나요?

 이런 질문들에 답하기 위해서는 아무래도 세다에 대한 엄밀한 정의가 필요해보입니다. 그리고 이를 위해서 우리가 먼저 알아야할 개념이 있죠…

 바로 함수입니다.

함수 (Function)

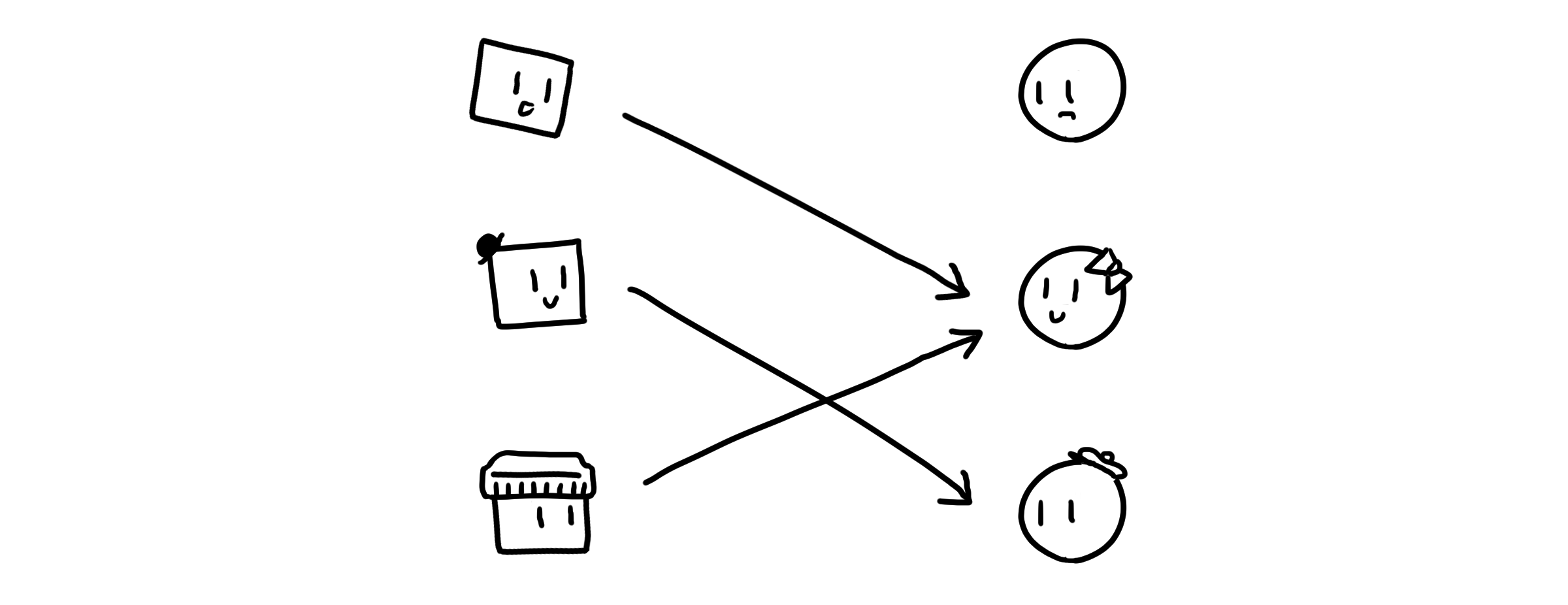
 새내기들이 학과 소개팅을 나갔습니다. 남학생들과 여학생들이 만나 운명의 상대를 짝짓겠죠! 여기서 남학생들은 각자 ‘제일’ 마음에 든 여학생을 지목하기로 합니다.

 그렇다면 남학생들의 선택은 여학생 중 한 명에게 향하는 화살표로 나타낼 수 있겠습니다. 한 사람만 지목할 수 있으므로, 남학생 한 명당 하나의 화살표 밖에 생기지 않아요.

 이렇게 남학생의 집합을 $A$, 여학생의 집합을 $B$라고 할 때, $A$의 원소가 $B$의 원소 중 정확히 하나에만 대응되는 관계를 함수라고 합니다. 함수 이름이 $f$일 때, 수식으로 쓰자면 아래와 같이 나타낼 수 있습니다.

\[f: A \rightarrow B\]

 여기서 집합 $A$를 정의역(Domain), 집합 $B$를 공역(Codomain)이라고 합니다. 함수에서 맺어지는 관계는 모두 순서쌍 $(x, y) \; (x \in X, y \in Y)$로 나타낼 수 있으므로, 함수는 두 정의역과 공역의 카르티시안 곱의 부분집합으로 볼 수도 있습니다.

함수의 대응관계

 갑자기 함수에 대해 설명하게 된 이유가 이것입니다. 함수의 대응관계중에는 몇 가지 특수한 경우가 존재합니다.

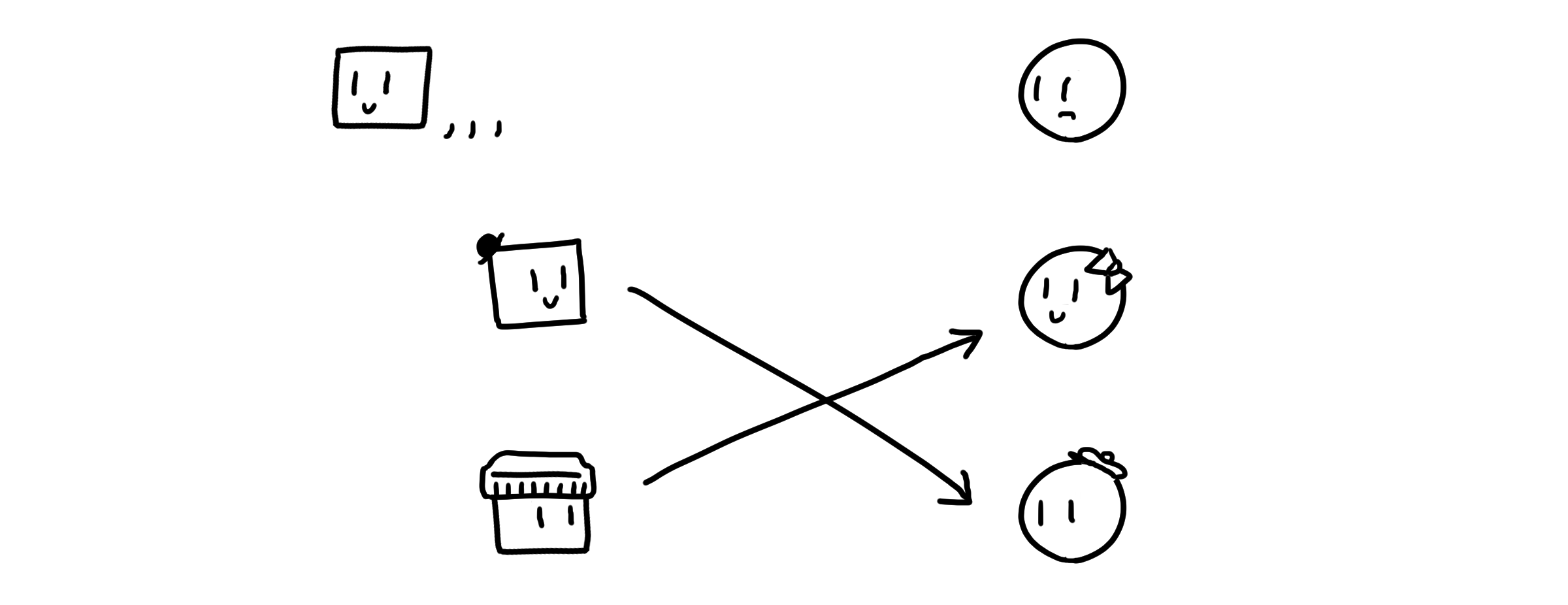
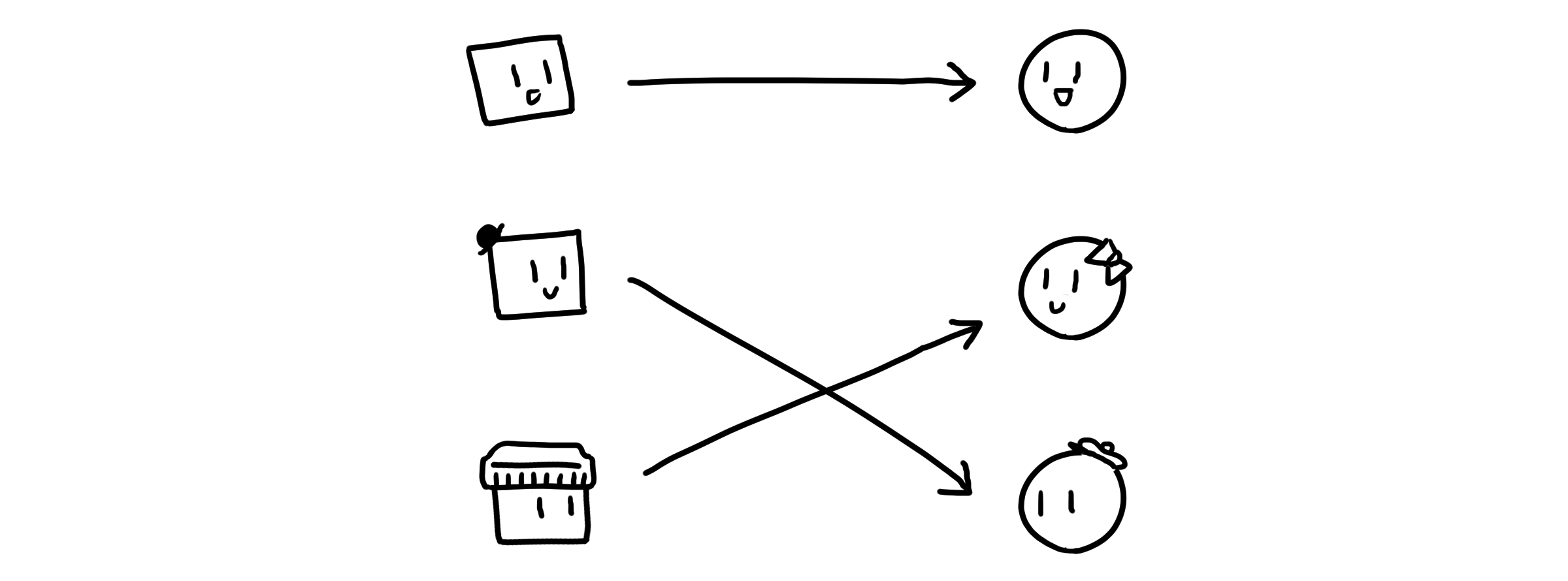
 일대일 함수(One-to-One, Injective)는 서로 다른 정의역 값이 항상 서로 다른 공역 값으로 대응되는 관계입니다. 같은 값을 집어 넣으면 같은 값이 나와야 하고, 다른 값을 집어 넣으면 다른 값이 나와야 합니다. 예컨대, 남학생들이 여학생들보다 수가 적더라도 남학생들의 선택이 겹치지만 않으면 일대일 함수라고 볼 수 있습니다.

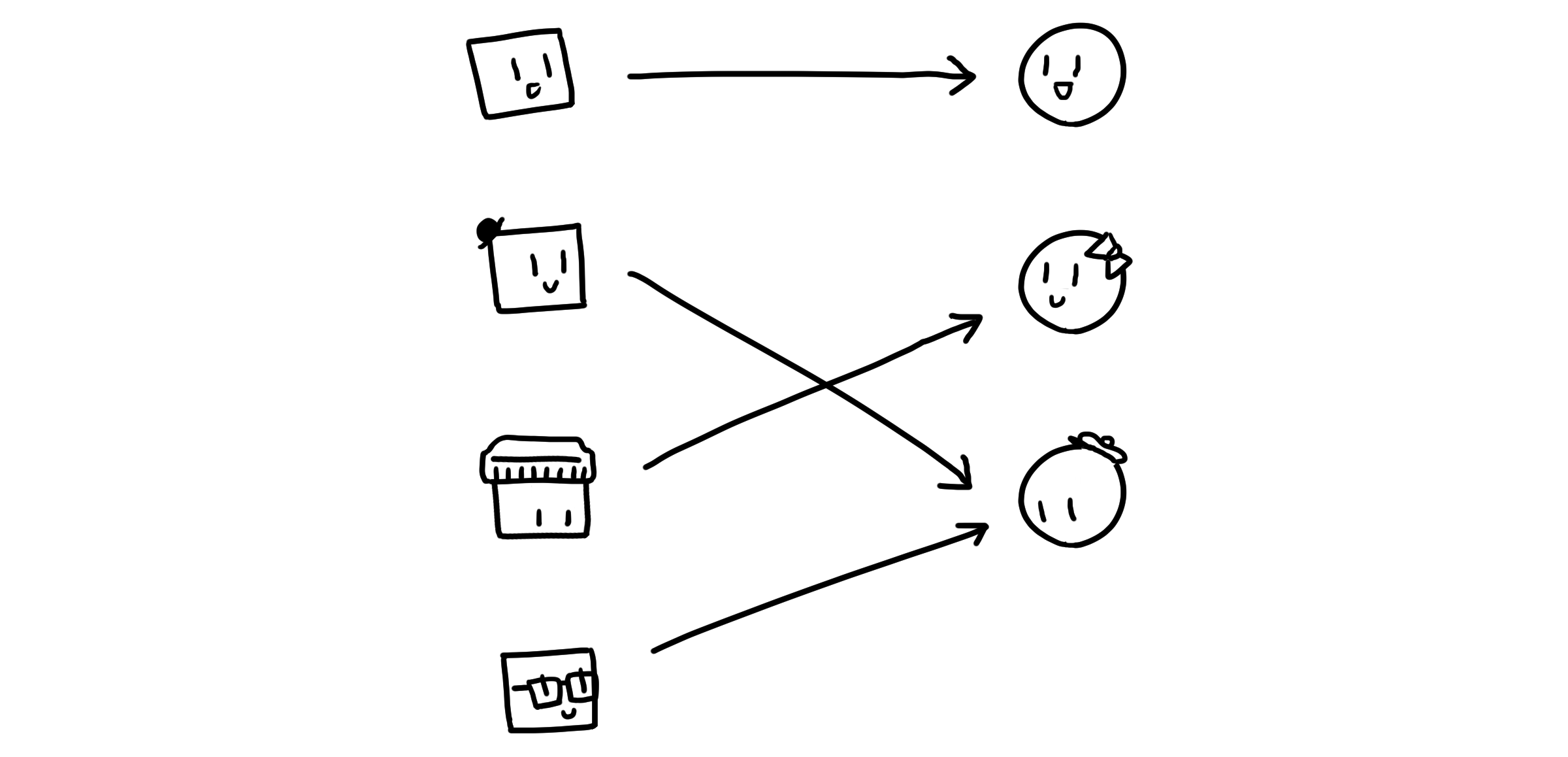
 전사 함수(Onto, Surjective)는 공역의 모든 값이 적어도 하나의 정의역 값과 대응되는 관계입니다. 정의역의 모든 값을 다 넣는다면, 반드시 공역의 모든 값이 나와야 합니다. 갑자기 남학생이 한 명 더 난입해 여학생을 지목해도, 여전히 모든 여학생이 지목받은 상태라면 전사 함수라고 할 수 있습니다.

 전단사 함수(One-to-One Correspondence, Bijective)는 일대일 함수와 전사 함수를 모두 만족하는 대응관계입니다. 즉, 정의역의 서로 다른 값이 서로 다른 공역의 값을 내면서 동시에 모든 공역의 값이 대응되어야 합니다.

집합의 크기 비교 (Cardinality)

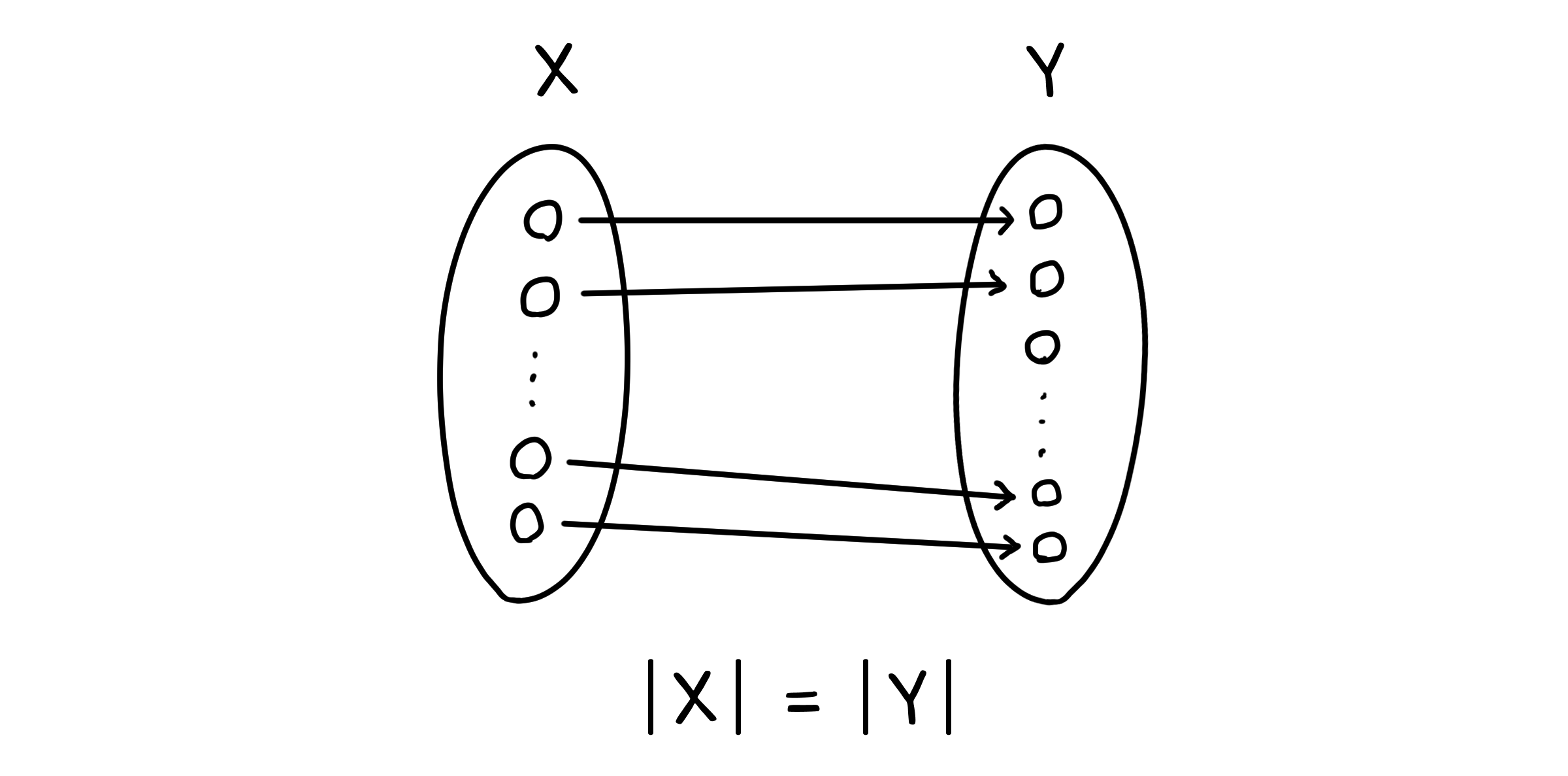
 네, 중요한 것은 이 전단사(일대일 대응)입니다! 일대일 대응을 이용하면 집합의 크기와 집합 사이의 크기 비교를 좀 더 엄밀하게 정의할 수 있습니다. 우선 알아야 할 것은, 두 집합 사이에 일대일 대응이 가능하면 두 집합의 크기는 같다는 것입니다.

 이제 우리는 앞서 이야기 했던 유한집합과 무한집합을 다시 정의할 수 있습니다. 바로 자연수의 집합과 그 크기를 비교하는 것이죠.
 만약 주어진 집합이 n이하의 자연수의 집합 ${1, 2, …, n}$과 일대일 대응이 된다면, 그 집합은 크기 n의 유한집합입니다. 반대로 어떤 n에 대해서도 해당 자연수 집합과 일대일 대응이 되지 않는다면, 그 집합은 무한집합입니다. 그런 관계로, 자연수 집합 $\;\mathbb{Z}^+$는 무한집합입니다.

셀 수 있는 집합

 일대일 대응을 사용하면 무한집합도 그 크기를 다룰 수 있게 됩니다. 집합에서 정의하는 셀 수 있는 집합(Countable)은 1. 유한집합이거나, 2. 자연수 집합 $\;\mathbb{Z}^+$과 크기가 같은(일대일 대응이 가능한) 무한집합입니다. 즉, 각 원소마다 번호를 매길 수 있다면 무한집합도 셀 수 있게 되는 것이죠.

 그런 관계로, 자연수 집합 $\;\mathbb{Z}^+$는 셀 수 있는 무한집합입니다. 셀 수 있는 무한집합의 크기는 $\aleph_0$라고 정의합니다. 즉, 모든 셀 수 있는 무한집합은 같은 크기를 가지게 됩니다.

$\aleph$는 알레프라고 읽으며, 히브리 문자의 첫 번째 글자입니다

무한집합 세 보기

 자연수와 일대일 대응이 가능하면 무한집합도 셀수 있다는 사실을 알았습니다! 그렇다면 더 큰 수 체계(정수나 유리수 같은 것들)의 집합도 셀 수 있지 않을까요?

 애석하게도, 증명은 좀 더 엄밀해야 합니다. 어떤 수가 어떤 자연수와 대응되는지(몇 번을 부여받을 것인지) 명확히 해야 하는 것이죠.

정수 세 보기

 먼저 예시로 정수 집합이 셀 수 있는지 알아봅시다.

 사실은 셀 수 있어요.

 아래와 같이 정수들을 재정렬 해봅시다.

\[F(n) = \begin{cases} \dfrac{n}{2}, & n \text{이 짝수일 때} \\[6pt] -\dfrac{n - 1}{2}, & n \text{이 홀수일 때} \end{cases}\]

 이렇게 규칙을 정하면, 우리는 모든 정수가 어떤 자연수에 대응하는지 알 수 있습니다. 즉, 자연수 집합과 일대일 대응이 가능해지는 것이죠. 정수 집합은 셀 수 있는 무한집합이었습니다!

유리수 세 보기

 그러면 유리수는 똑같이 셀 수 있을까요?

 사실 이것도 정렬을 잘 하면 되긴 합니다.

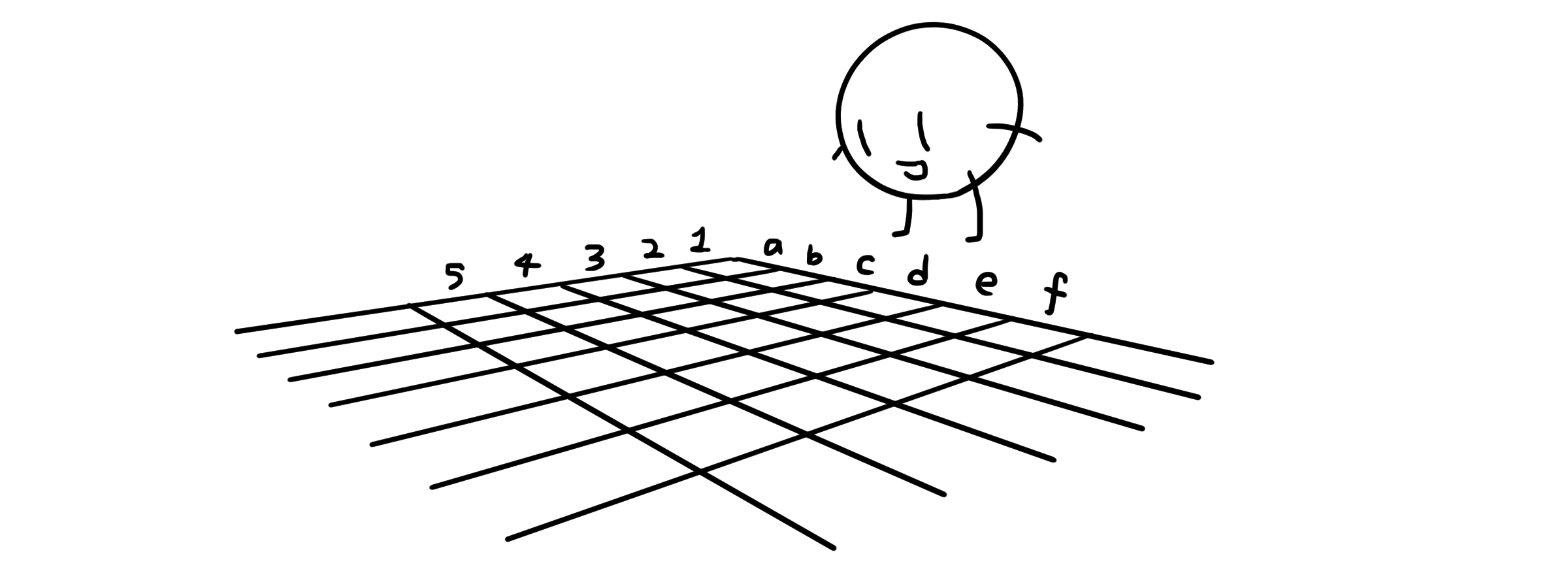
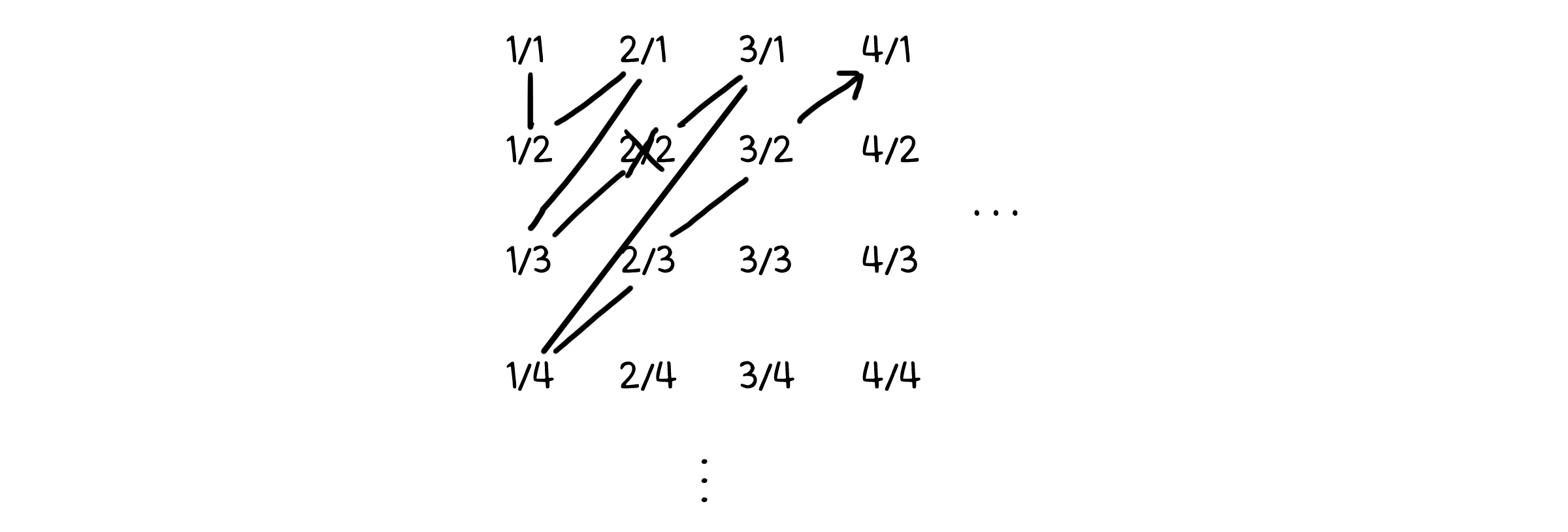
 조금 복잡한 방법을 사용해봅시다. n번째 행은 분모가 n, m번째 열은 분자가 m이 되도록 분수들을 2차원 배열로 나열하였습니다. 이렇게 하면 끝없이 나열된 배열에 모든 양의 유리수를 늘어 놓을 수 있습니다.

 이제 1/1부터 시작해 지그재그를 그리며 분수들에 번호를 매기면(물론 약분 가능한 수는 건너뛰고요), 모든 양의 유리수는 자연수와 대응할 수 있습니다. 동일한 방법으로 음의 유리수도 자연수와 일대일 대응이 가능하다는 것을 알 수 있습니다.

 마지막으로 아래 정리를 사용하면, 유리수 집합 또한 셀 수 있는 무한집합임을 보일 수 있습니다!

Theorem 1.
집합 $A$와 $B$가 셀 수 있는 집합이면, $A \cup B$ 또한 셀 수 있는 집합이다.

실수 세 보기

 마지막으로 실수도 똑같이 셀 수 있을까요?

 아뇨, 셀 수 없습니다.

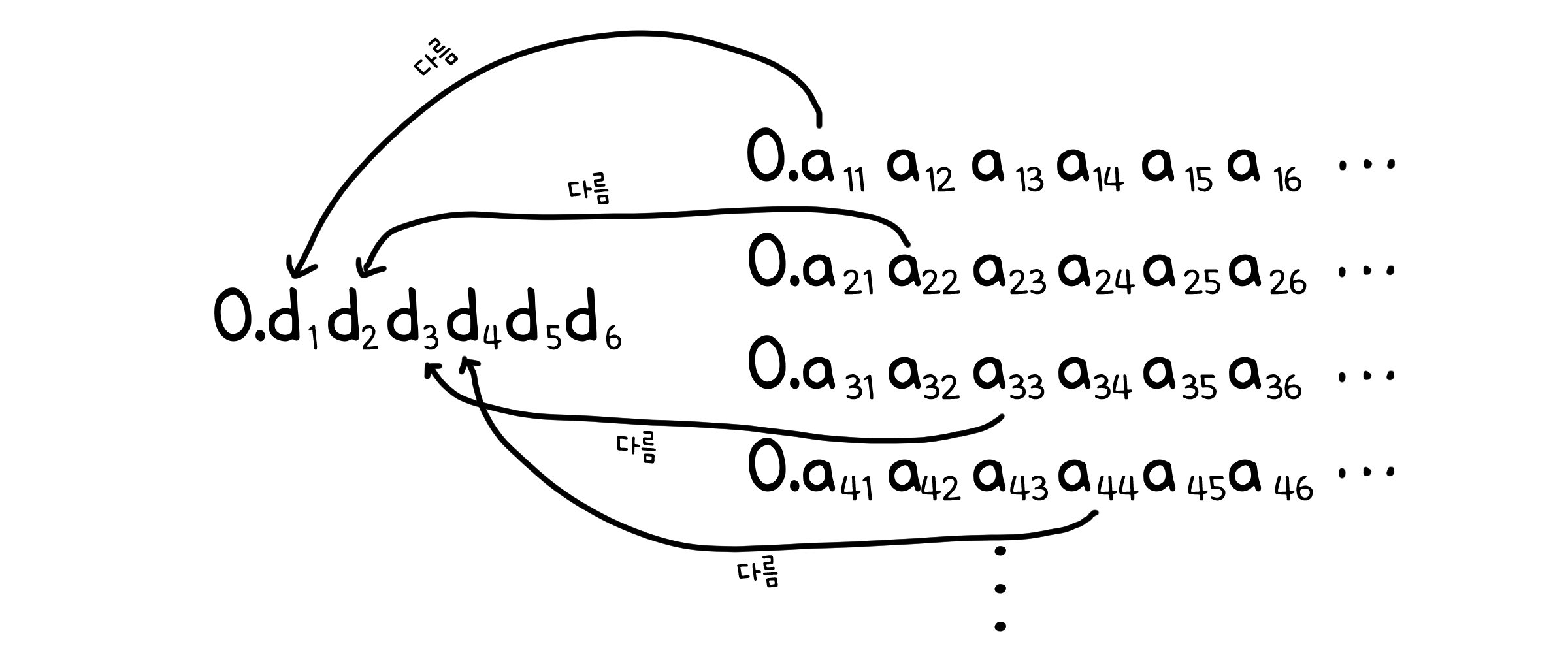
 어째서인지 0과 1사이의 실수의 경우를 통해 설명하겠습니다. 일단 0과 1사이의 실수의 집합이 셀 수 있다고 가정해봅시다. 그렇다면 우리는 어떻게든 정렬이 된 수많은 소수들을 이렇게 나열할 수 있을 것입니다. $a_{nm}$은 n번째 실수의 소수점 m번째 자리의 숫자를 나타냅니다.

 이제 우리는 특별한 규칙으로 새로운 수 d를 만들어 볼 것입니다. d는 똑같이 0과 1사이의 실수이며, 각 소수점 n번째 자리의 숫자는 이렇게 정의합니다.

\[d_n = \begin{cases} 0, & a_{nn} \neq 0 일 때 \\[6pt] 1, & a_{nn} = 0 일 때 \end{cases}\]

 이렇게 하면 d는 0.110010110… 과 같은 값을 가지게 되겠죠. 이게 뭐가 특별하냐구요? 이제 d를 앞서 나열한 소수들과 비교해봅시다. 그러면 n번째 소수를 d와 비교했을 때 반드시 소수점 n번째 자리의 숫자가 같아질 수 없다는 것을 알 수 있을 것입니다. 왜냐면, 애초에 d를 그렇게 되도록 만들었으니까요!

 따라서 d는 나열한 그 어떤 소수에도 해당하지 않는 새로운 수임을 알 수 있습니다. 아니, 셀 수 있는 모든 0과 1사이의 실수를 나열했는데, 그 속에 해당하지 않는 수가 나왔네요? 우리는 여기서 모순을 발견하게 됩니다. 그러므로 가정은 거짓, 0과 1사이의 실수는 셀 수 없음을 증명하였습니다.

 아쉽지만 숫자 세는 일은 여기까지 해야 할 것 같네요.