[CM201] 03. 증명(Proof)

명제를 엮어 논리로 만들기

 우리가 명제에 대해 이야기한 이유는 궁극적으로 논리를 펼치기 위함이었습니다. 이제 명제들을 이용해 논리를 만드는 법에 대해 이야기해봅시다. 논리의 가장 기초적인 구조는, 어떤 전제들을 바탕으로 새로운 결론을 끄집어내는 것입니다.

논증 (Argument)

 논증은 명제들의 나열입니다.

 단, 단순히 늘어놓은 것이 아니라 전제(Premise)와 결론(Concluion)이 명확이 나뉘어져 있어야 합니다.

 만약 전제들이 모두 참일 때 결론이 반드시 참이 될 수 밖에 없다면, 그 논증은 타당하다(Valid)라고 합니다.

• 2=3이면, 나는 모자를 먹는다
• 나는 모자를 먹었다
• 그러므로 2=3이다.

 이 논증은 타당하지 않다고 할 수 있죠.

몇 가지 추론의 규칙들

 논증 중에서는 당연히 여겨지면서도 추론과정에서 많이 쓰이는 패턴들이 존재합니다. 그리고 일부는 이름도 따로 가지고 있죠.

증명 (Proof)

 마침내 논증을 사용해 논리적 주장을 펼칠 때가 왔습니다. 전제부터 결론까지 나열된 명제들로 여러분의 생각을 증명할 순간이죠! 하지만 앞선 논증에서 보았듯이 논리의 전개는 엄밀하고 신중해야 합니다… 어쩌면 몇 가지 요소들이 우리의 생각을 엄밀히 하는데 도움을 줄지도 몰라요.

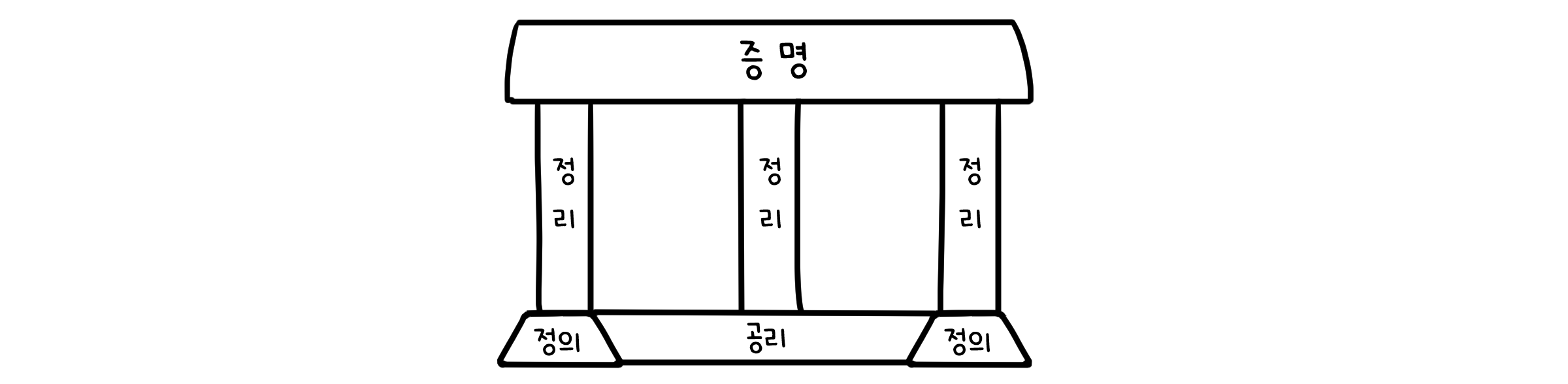
기본요소 - 공리, 정의, 그리고 정리

 공리(Axiom)는 증명 없이 참으로 받아들이는 기본 명제입니다. 이것들은 여지 없이 참이라고 합의를 한 것이니, 안심하고 마음껏 사용해도 됩니다.

• 두 점을 지나는 하나의 직선이 존재한다.
• 모든 수 a에 대해서 a = a이다.

 정의(Definition)는 기존에 존재하던 것들을 이용해 새로운 개념이나 용어에 대해 설명한 것입니다. 다 같이 정한 사회적 약속이기 때문에, 공리처럼 명제를 참으로 받아들인다는 개념과는 다릅니다. 사전에 등재된 단어 같은 것이죠.

• 짝수란 2로 나누어 떨어지는 정수를 말한다.
• 소수란 1과 자기 자신 외에는 약수가 없는 정수이다.

 정리(Theorem)는 공리와 정의에서부터 논리적으로 도출 가능한 참인 명제입니다. 여기서부터는 합의된 것이 아니기 때문에 사실로부터 추론해야하는 영역입니다.

• 소수는 무한하다.
• 삼각형 내각의 합은 180도이다(유클리드 기하학에서!)

 정리에는 보통 보조정리(Lemma)나 따름정리(Corollary)가 함께 등장합니다.

• 보조정리 : 정리를 증명하기 위해 먼저 보여야 하는 작은 정리
• 따름정리 : 증명된 정리로부터 자연스럽게 따라오는 또 다른 정리

여러 가지 증명 방법들

 증명의 위에서 언급한 공리, 정의, 그리고 이미 증명된 정리들을 적절히 조합함으로서 이뤄집니다. 처음에 주어진 조건을 수식으로 나타낸 뒤 적절한 방법으로 전개하여 결론에 도달하는 방식이 제일 평범하고 일반적입니다. 하지만 경우에 따라서 우리는 다양한 방법을 시도해볼 수 있습니다.

반례 (Counterexample)

 만약 주어진 명제가 거짓임을 증명해야 한다면, 그 명제를 만족하지 않는 반례를 찾아 거짓임을 증명하는 방법도 있습니다.

대우 (Contrapositive)

 증명하기 까다로운 명제가 있다면, 그 대우를 증명하는 방법도 있습니다. 대우는 기존 명제에서 가정과 결론의 자리를 바꾼 후, 각각을 부정한 명제입니다. 대우는 원래 명제와 동치이기 때문에, 대우가 참임을 증명하는 것이 곧 원래 명제가 참임을 증명하는 것입니다.

\[p \rightarrow q \quad \equiv \quad \neg q \rightarrow \neg p\]

귀류법 (Contradiction)

 명제를 한 번 부정해보는 것도 방법이 될 수 있습니다. 주어진 명제와 반대되는 명제가 참이라고 가정한 뒤 논리를 펼치다보면, 어느샌가 모순이 발생한다고 설명하는 것이죠. 그렇다면 가정한 명제는 참일 수가 없으니, 원래 명제가 참이 되는 것입니다.

경우의 수 (Cases)

 명제의 가정이 다시 여러 개의 명제로 나뉘어져 있다면, 각각을 나누어 경우에 따라 증명을 할 수 있습니다. 한 번에 전체 경우를 다루기 까다로울 수 있기 때문에, 작은 경우만을 따로 생각하는게 편리할 수 있습니다.

\[(p_1 \vee p_2 \vee ... \vee p_n) \rightarrow q \quad \equiv \quad (p_1 \rightarrow q) \land (p_2 \rightarrow q) \land ... \land (p_n \rightarrow q)\]

몇 가지 시나리오

존재성 증명 (Existence proof)

 만약 특정 조건을 만족하는 경우 있음을 보여야 하는 증명이라면, 두 가지 방법으로 증명할 수 있습니다. 직접 해당 조건을 만족하는 경우를 찾는 방법(Constructive existence proof)이 있고, 존재한다는 것 까지만 보이고 그것이 무엇인지는 굳이 찾지 않는 방법(Nonconstructive existence proof)이 있습니다(어쨋거나 있다는 사실이 중요하니까요!).

동치 증명 (Equivalence proof)

  이전에 $p \leftrightarrow q$가 항상 참이면 q와 p는 동치라고 했습니다. 따라서 p와 q에 대한 쌍조건문이 참임을 증명하면 됩니다. 그리고 쌍조건문은 다시 두 명제의 논리곱으로 나타낼 수 있으므로, 이 명제들이 참임을 보이면 됩니다.

\[p \leftrightarrow q \quad \equiv \quad (q \rightarrow p) \land (p \rightarrow q)\]

적절한 증명 방식 찾기

  대표적인 방법 몇 가지를 소개하였지만, 사실 더 많은 증명 방법이 있을 수도 있습니다. 모든 경우에 먹히는 증명방식이란 것은 없으니까요. 어떤 명제를 증명하는데 어떤 방법을 사용하는지는, 순전히 여러분의 직관에 달려 있습니다.

아님 말고요.