[CM201] 02. 논리(Logic)

논리에 대하여

 이산수학은 추론의 연속입니다. 그리고 추론에 반드시 필요한 것은 논리죠. 사전에서 논리는 말이나 글에서 사고나 추리 따위를 이치에 맞게 이끌어 가는 과정이나 원리라고 설명합니다. 중요한 것은 이치에 맞게 이끌어간다는 것입니다. 시작점이 있고 도착점이 있으며, 그 사이에는 정해진 단계가 있다는 것이죠.

 우선 이 단계에 해당하는 단위인 명제에 대해 알아보고, 그 다음 장에서는 이를 연결하는 과정에 대해 알아볼 것입니다.

명제 (Proposition)

 명제는 논리를 이루는 가장 기본적인 단위입니다.

 일단 명제는 문장입니다. 거기에다가 선언적인 문장(declarative sentence)이기 때문에, 반드시 참이나 거짓 둘 중 하나로 판단할 수 있어야 하죠. 참 거짓이 모호하거나, 사람에 따라 그 판단이 바뀌어서는 안됩니다.

복합 명제 (Compund Proposition)

 명제는 가장 기본적인 단위라고 했었죠. 그 말은 명제로 서로 합쳐 더 큰 무언가를 만들 수도 있다는 뜻입니다. 명제와 명제를 합치면 더 긴 명제가 됩니다. 이렇게 두 명제가 있다고 합시다.

• p : 지금은 비가 온다.
• q : 지금은 춥다.

 이 두 명제를 이런 식으로 합칠 수 있습니다.

• p 이고 q : 지금은 비가 오면서 춥다.
• p 이거나 q : 지금은 비가 오거나 춥다.
• p 이고 q가 아님 : 지금은 비가 오지만 춥지 않다.
• p가 아니거나 q : 지금은 비가 오지 않거나 춥다.
• 등등…

 여기서 자주 등장하는 단어를 볼 수 있을 겁니다. 이고, 이거나, 아님이 그것이죠. 이들은 모두 명제를 조합하는데 있어서 가장 기본적인 논리 연산입니다.

단어	연산	연산자
아니다	부정 (Negation)	¬p
이고	논리곱 (Conjunction)	p ∧ q
이거나	논리합 (Disjunction)	p ∨ q

조건 명제 (Conditional Proposition)

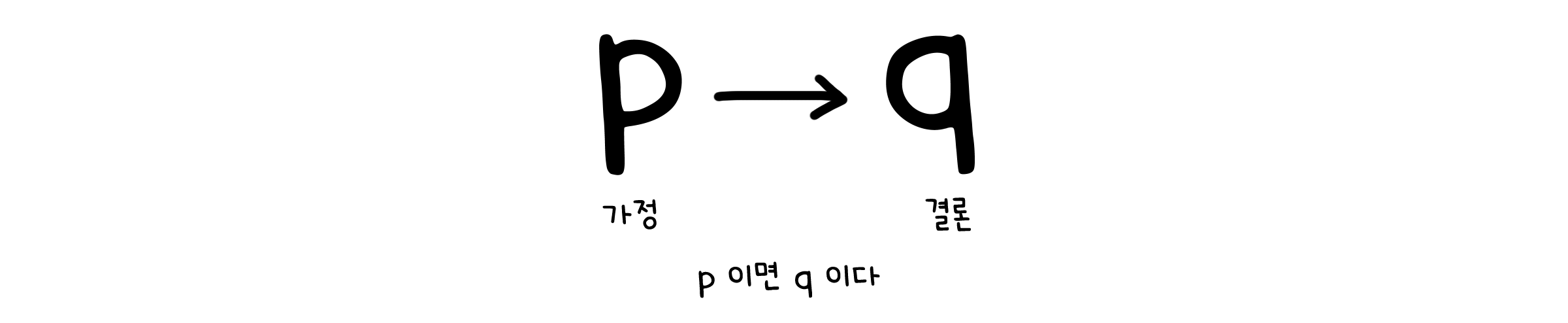
 조금 더 복잡한 명제를 만들어 볼까요? 이번에는 조건을 앞에 붙입니다. 물론 그 조건도 다른 명제로 이루어져 있죠. 이렇게 어떤 명제(p)가 참일 때 다른 명제(q)도 참이다를 표현한 명제를 조건문(Conditional statement)이라고 합니다. 이 때 앞의 명제(p)를 가정, 뒤의 명제(q)를 결론이라고 합니다.

 일반적으로 조건문은 가정이 참이라고 전제하고 결론이 참인지 거짓인지를 판별하는 경우가 많습니다. 당연히 결론이 참일 때 조건문은 참, 결론이 거짓일 때 조건문은 거짓이 되겠죠.
 그렇다면 가정이 거짓, 그러니까 애초에 전제가 틀렸다면 조건문의 참거짓은 어떻게 될까요? 이 경우 전제조건 자체가 잘못되었기 때문에 조건문은 참입니다. 조건문이 거짓이라면 그 예시(반례라고 합니다)를 찾아줘야 하는데, 전제가 틀린 상태라 예시를 들 수가 없거든요.

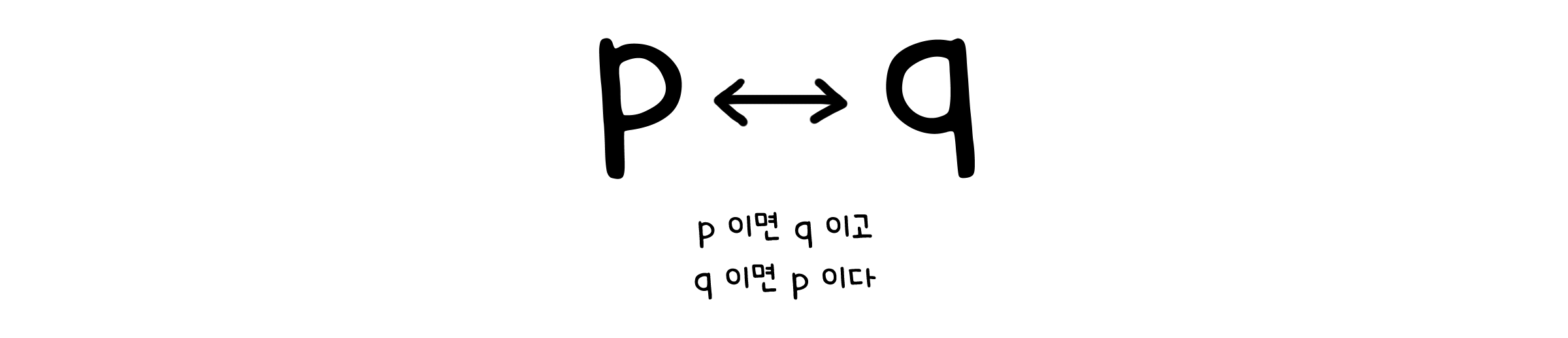
 가정과 결론이 없이 두 명제가 서로에게 조건이 되는 명제는 쌍조건문(Biconditional statement)이라고 합니다. 쌍조건문은 두 명제가 모두 참이거나 모두 거짓일 때만 참이 됩니다.

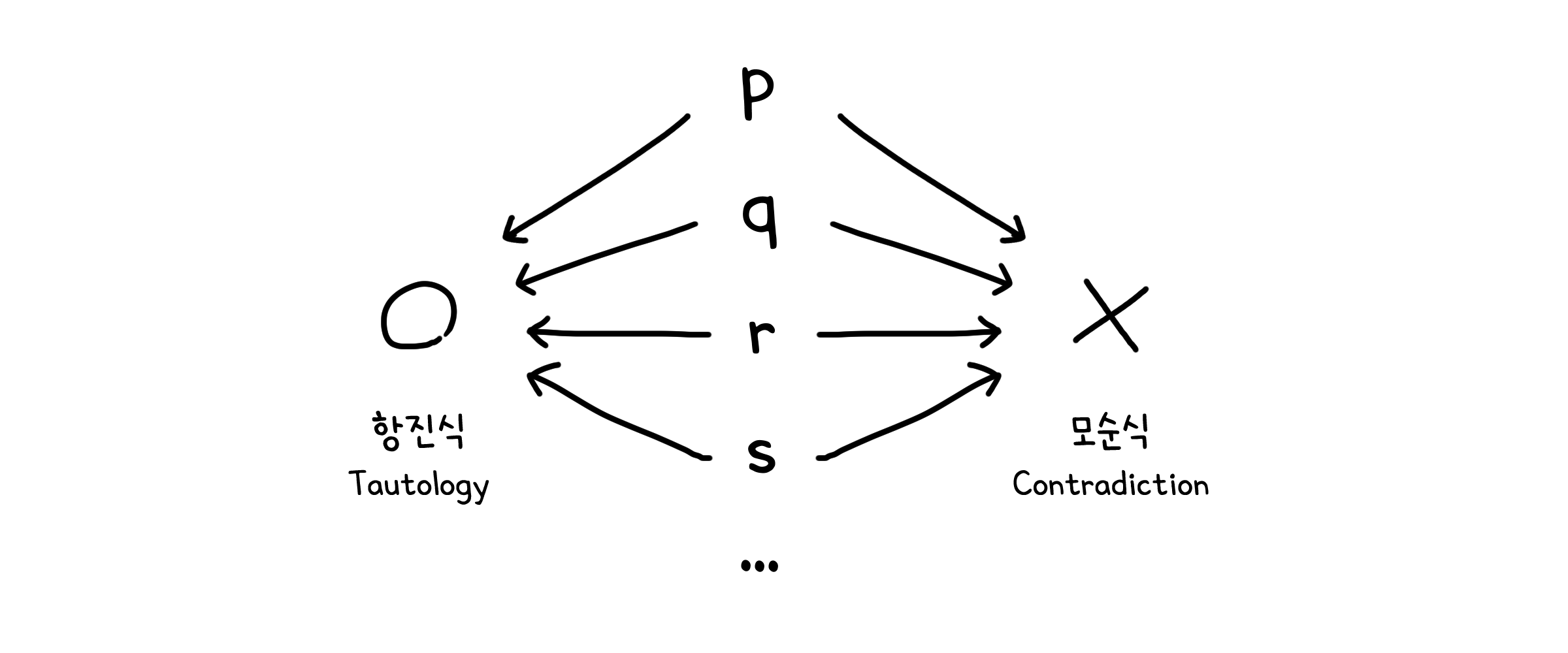
항상 똑같은 명제들

 조건과 관계 없이 항상 참인 명제를 항진식(Tautology), 반대로 항상 거짓인 명제를 모순식(Contradiction)이라고 합니다.

나머지 명제들은 평범이들입니다. 조건에 따라 참이 될 수도, 거짓이 될 수도 있죠. 만약 명제가 참이 되도록 하는 조건이 존재한다면, 그 명제는 만족가능하다(Satisfiable)고 합니다. 반대로 어떻게 해도 명제가 참이 되지 않으면 만족가능하지 않다(Unsatisfaiable)라고 합니다. 모순식과 같죠.

동치 (Equivalence)

 동치는 ‘같다’라는 말은 좀 더 논리학적 맥락에서 말하고 싶을 때 사용하는 말입니다. 물론 수학적 용어인 만큼 그 정의가 조금 더 엄밀하긴 합니다.

명제적 동치 (Propositional equivalence)

 앞서 다루었던 명제의 맥락에서 정의한 동치입니다. 두 명제를 비교할 때 사용하는데, 단순히 모든 경우에 대하여 두 명제가 같은 값(참 또는 거짓)을 가지면 두 명제는 동치라고 할 수 있습니다. 주먹구구식이어서 다소 표면적이고 기계적인 접근으로 보일 수 있습니다.

논리적 동치 (Logical equivalence)

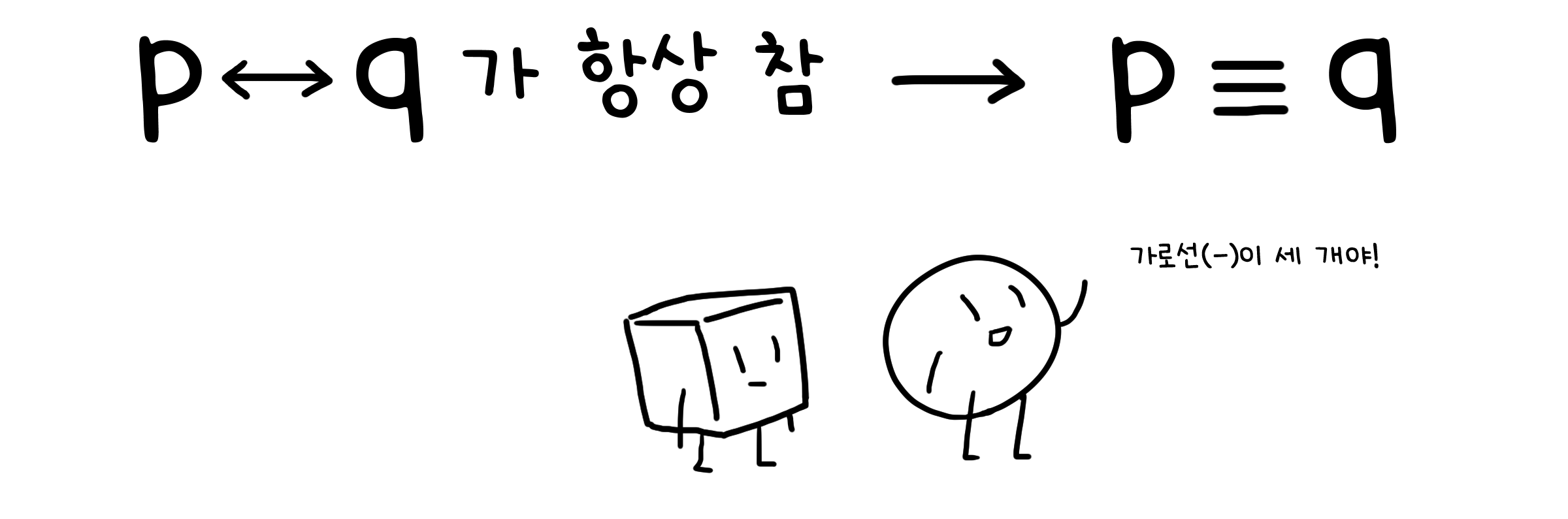
 좀 더 수학적이고 논리적인 맥락에서 정의한 동치입니다. 어떤 두 명제 $p$와 $q$가 있을 때, $p \leftrightarrow q$가 항진식이면(=항상 참이면) 두 명제는 동치라고 하며, 이를 수학기호 $p \equiv q$로 표기합니다. 이전에 소개했던 조건문의 형태로 쓴다면, 이렇게 나타낼 수 있겠죠.

논리적 동치임을 증명하는 과정에서 명제적 동치임을 활용해도 됩니다. 그러니까, 모든 경우를 따져서 $p \leftrightarrow q$가 항진식임을 보여도 된다는 뜻입니다. 주먹구구식이지만, 그 만큼 확실하고 단순합니다!
대표적인 예로 $p \rightarrow q$ 와 $\neg p \vee q$ 가 동치임을 보일 수 있습니다. 모든 $p$와 $q$의 경우(총 네 가지)에 대해 두 명제의 참/거짓 값을 비교해보면 쉽게 증명할 수 있습니다.

술어 (Predicate)

 이때까지는 참 또는 거짓 중 하나로 판단할 수 있는 완전한 문장만을 다루었습니다. 하지만 현실은 올곧지 않습니다. 대부분 변수를 포함하기 마련이죠. 때문에 명확하게 참/거짓을 결정할 수 없는 문장들이 많습니다.

x는 홀수이다.

 이 문장은 어떤가요? 우리는 x의 값을 모르니, 이 문장이 참인지 거짓인지 섣불리 판단할 수 없습니다. 이렇게 하나 이상의 변수를 포함하고 있어 그 값에 따라 참 또는 거짓이 되는 문장을 술어(Predicate)라고 합니다. 변수에 따라 명제가 하나씩 대응되기 때문에 명제함수(Propositional function, $P(x)$)라고 부르기도 합니다.

양화사 (Quantifier)

 술어는 특정한 범위의 변수들을 가집니다. 그 범위는 모든 정수, 어떤 자연수 등 술어에 따라 다양하게 정의될 수 있는데, 이런 범위를 특정할 수 있게 하는 기호를 양화사(Quatifier)라고 합니다.

 전칭양화사(Universal Quantifier)는 모든 x에 대하여라는 의미입니다. x에 포함된 모든 값의 명제가 참이면, 술어는 참입니다. x에 포함된 값 중 하나라도 명제가 거짓이면, 술어는 거짓입니다.

 존재양화사(Existential Quantifier)는 어떤 x에 대하여라는 의미입니다. x에 포함된 값 중 하나라도 명제가 참이면, 술어는 참입니다. x에 포함된 모든 값의 명제가 거짓이면, 술어는 거짓입니다.

양화사 부정하기 (Nagating quantifier)

 두 양화사는 부정을 하면 서로 반대 양화사로 변합니다.

\[\begin{align} \neg \; \forall x \; P(x) \; \equiv \; \exists x \; \neg P(x) \\ \neg \; \exists x \; P(x) \; \equiv \; \forall x \; \neg P(x) \end{align}\]

 ‘모든 쿠키는 초콜렛이 들어 있다’라는 문장을 부정하고 싶으면 어떻게 해야 할까요? 초콜렛이 들어있지 않은 쿠키를 찾아 보여주면 되겠죠. ‘초콜렛이 없는 쿠키가 존재한다’, 다르게 말하면 ‘어떤 쿠키는 초콜렛이 들어있지 않다’가 되는 것입니다. 반대로 마찬가지입니다. ‘어떤 쿠키는 비누가 들어있다’를 부정하고 싶으면 전 세계 모든 쿠키를 가져와 비누가 들어있지 않음을 보여주어야겠죠. ‘모든 쿠키는 비누가 들어있지 않다’가 되는 것입니다.

양화사 같이 쓰기 (Nested Quantifier)

\[\begin{align} \neg \; \forall x \; \exists y P(x, y) \\[8pt] \neg \; \exists x \; \forall y P(x, y) \end{align}\]

 변수가 여러 개라면, 두 양화사를 함께 쓸 수도 있습니다. ‘모든 쿠키에는 사용되는 토핑이 존재한다’라는 문장을 생각해봅시다(아무것도 없는 밋밋한 쿠키는 잠시 치우고요). 변수는 쿠키와 토핑 두 가지입니다. 그리고 쿠키는 모든, 토핑은 존재한다라는 조건이 있습니다. 그러므로 이를 술어로 나타낼 수 있습니다. 두 양화사를 바꾸면 어떻게 될까요? ‘어떤 쿠키는 모든 토핑을 사용한다’라는 문장이 됩니다. 양화사만 바꾸었을 뿐인데 상당히 다른 의미의 문장이 되었죠.

 이때까지 명제와 술어에 대해 정리해보았으니, 다음은 이들을 어떻게 연결하여 논리를 펼칠 수 있는지에 대해 다뤄보겠습니다.