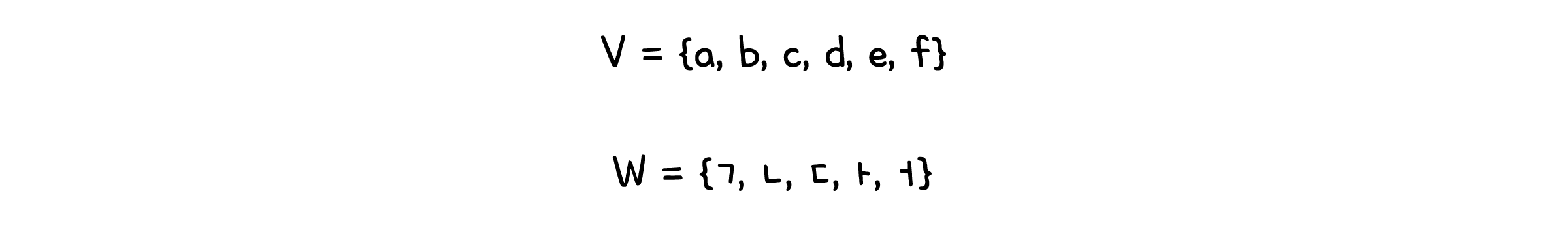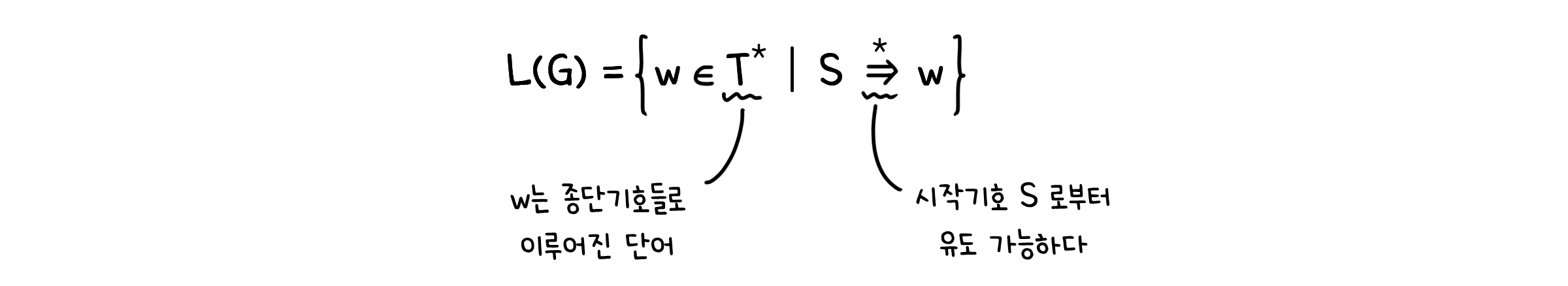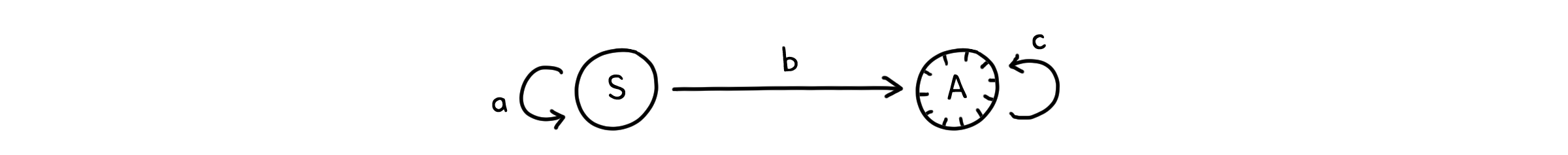[CM201] 11. 언어와 문법 (Language & Grammar)

 이전 장에서 지나가듯 들어 보았던 예시를 다시 살펴 봅시다.

 이 FSA가 무엇을 의미하는지는 쉽게 알 수 있었습니다. a와 b로 이루어진 문자열 중 a를 포함하는 것만 허용하는 것이었죠. 만약 b로만 이루어진 문자열을 입력한다면, 수용상태에 도착하지 못해 허용되지 않을 것입니다.

 FSA는 특정 문자들로 이루어진 문자열 중에서도 특별한 규칙을 만족하는 문자열만 허용합니다. 좀 더 일반적인 관점에서 생각해봅시다. ‘특정 문자들로 이루어진 문자열’, 우리는 이것을 단어(word)라고 부릅니다. 즉, FSA는 단어에 부여된 규칙을 검사하는 기계인 셈입니다. 그러니까 우리는 이 체계 자체를…

 문법이라고 볼 수 있지 않을까요?

문법 (Grammar)

 컴퓨터와 수학에 무슨 문법이 나오나 생각할 수 있겠지만, 놀랍게도 컴퓨터 과학에서도 특정한 형태의 언어와 문법에 대해 다루고 있습니다.

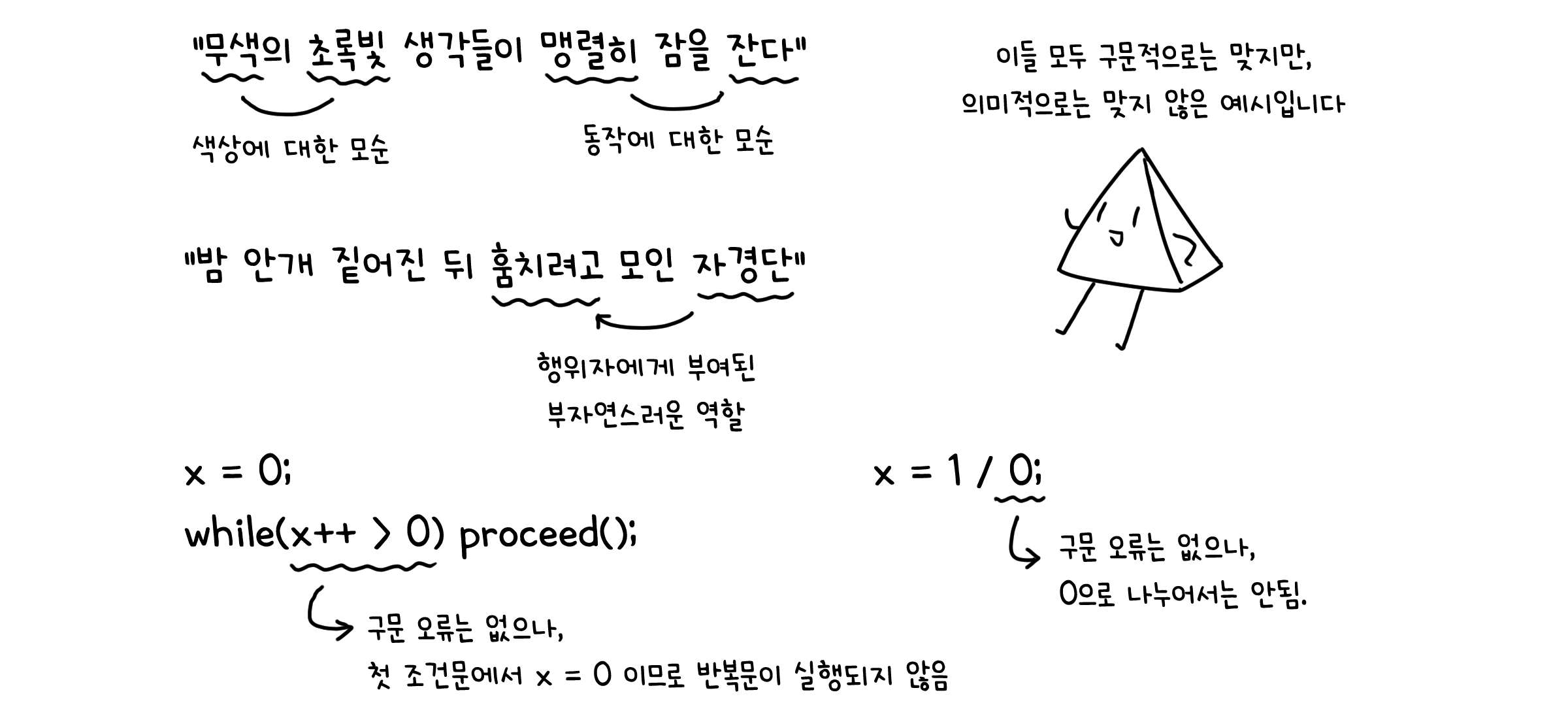
 문법은 언어를 정의하는 규칙입니다. 그리고 그 규칙은 두 가지 관점으로 나뉠 수 있는데, 구문(Syntax)과 의미(Semantics)의 관점입니다.

 구문(Syntax)은 언어의 구조적 타당성을 판별하는 요소입니다. 문장의 구조나 기능, 구성 요소 따위를 따져 해당 문장이 어법상 잘못되지 않았는지 판단하는 것이라고 볼 수 있습니다. 컴퓨터 과학에서의 구문도 마찬가지입니다. 사용하고자 하는 프로그래밍 언어의 문법 규칙을 잘 지키는지를 판단하게 되죠.

 의미(Semantics)는 언어의 의미적 타당성을 판별하는 요소입니다. 어법상 전혀 잘못된 부분이 없어도 문장 자체가 의미하는 바가 부자연스럽다면, 의미적 관점에서 잘못되었다고 생각할 수 있습니다. 컴퓨터 과학에서는 코드가 의도한 대로 동작하거나 올바른 의미를 전달하는지를 판단하게 됩니다.

몇 가지 기본적인 용어들

 언어를 이루는 가장 작은 단위는 기호(Symbol)입니다. 영어권 언어의 알파벳, 한국어의 한글자모 등이 여기에 해당합니다.

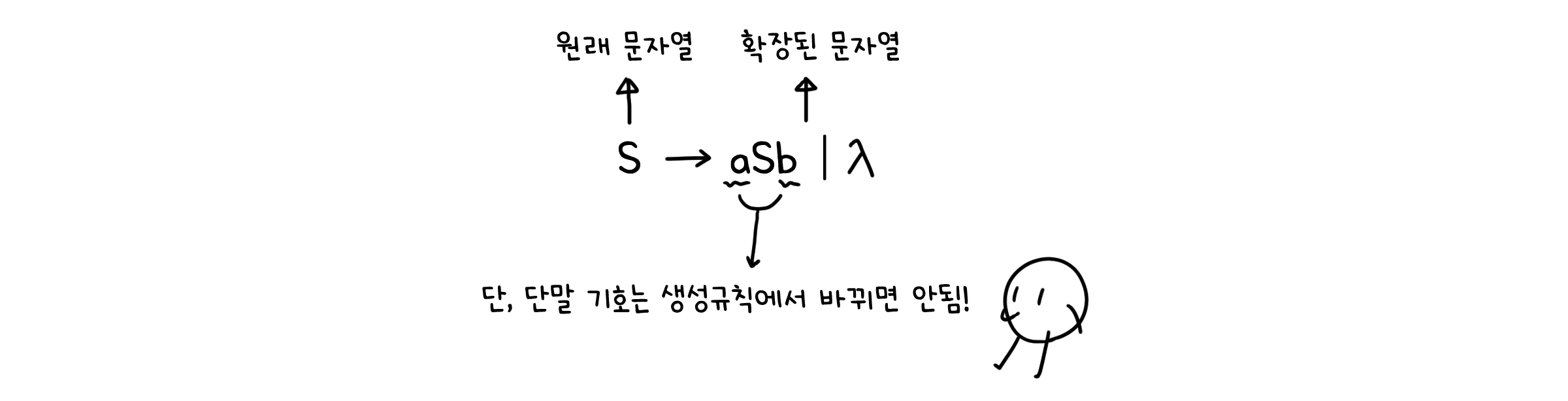
 기호들이 모여 만들어지는 문자열을 단어(Word)라고 합니다. 기호들의 집합 $V$로 만들어지는 모든 단어의 집합은 $V^{*}$라고 표기합니다. 어떠한 기호도 포함하지 않은 빈 문자열은 특별히 $\lambda$ 라고 표기합니다.

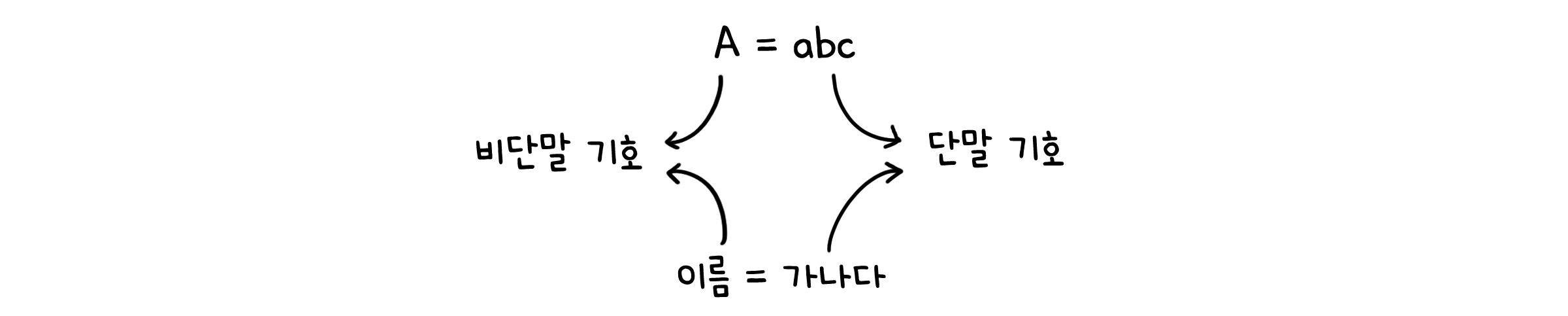
 더 이상 다른 값(기호)으로 나뉠 수 없는 기호를 단말 기호(Terminal symbol), 나뉠 수 있는 기호를 비단말 기호(Nonterminal symbol)라고 부릅니다.

 단어의 집합 $V^{*}$에 속하는 임의의 문자열로부터 새로운 문자열로 확장하는 방법을 생성규칙(Production)이라고 합니다. 일반적으로 원래 문자열 → 확장된 새로운 문자열과 같은 형식으로 표현합니다. 언어에 속한 문자열들은 모두 이 생성규칙으로 부터 유도가 가능합니다.

구문 구조 문법 (Phrase-Structure Grammars)

 위 용어들을 활용해 이산수학에서의 문법은 좀 더 엄밀하게 정의해봅시다. 아래 조건들이 있다면, 문법 $G$를 정의할 수 있습니다.

요소	의미	예시
$V$	기호들의 집합	${ a, b, A, B, S }$
$T$	단말 기호로 이루어진 하위집합	${ a, b }$
$S$	첫 시작 기호	$S$
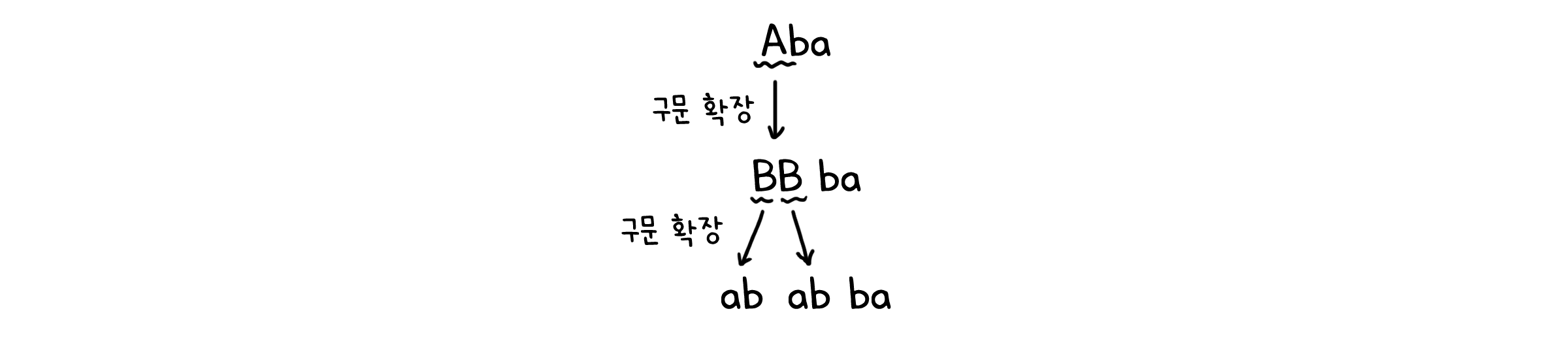
$P$	생성 규칙	${ S \rightarrow Aba, A \rightarrow BB, B \rightarrow ab, AB \rightarrow b }$

\[G = (V, T, S, P)\]

  정의된 문법 $G$는 이렇게 표기하며, 이를 구문 구조 문법(Phrase-Structure Grammars)이라고 합니다. 문법이 단어(Word) 단위로 확장되지 않고 기호들의 묶음, 즉 구(phrase) 단위로 확장되기 때문입니다.

언어 (Language)

 이산수학적으로 정의되는 언어는, 특정 단어 집합의 부분집합을 뜻합니다. 그 단어들은 역시 특정 기호들로 만들어지는 것들이어야 하고요. 언어 $L$이 단어의 집합 $X^{*}$의 부분집합으로 만들어졌다고 할 때, 기호 $X$ 위의 언어 $L$, 혹은 기호 $X$로 정의된 언어 $L$ (Language $L$ over $X$)이라고 합니다.

 만약 언어 $L$이 구문 구조 문법 $G = (V, T, S, P)$로 만들어졌다면, $L(G)$이라고 표기합니다.

정규 표현식 (Regular expression)

 정규 표현식(Regular expression)은 특정한 규칙을 가진 문자열들의 집합을 표현하는데 사용하는 언어입니다. 기호 $I$로 정의된 정규 표현식은 아래와 같이 재귀적으로 정의됩니다.

• $\emptyset$은 정규 표현식입니다. $\emptyset$은 어떠한 문자열도 포함하지 않은 상태를 의미합니다.

• $\lambda$는 정규 표현식입니다. $\lambda$는 빈 문자열 ‘ ‘을 의미합니다.

• $x \in I$는 정규 표현식입니다.

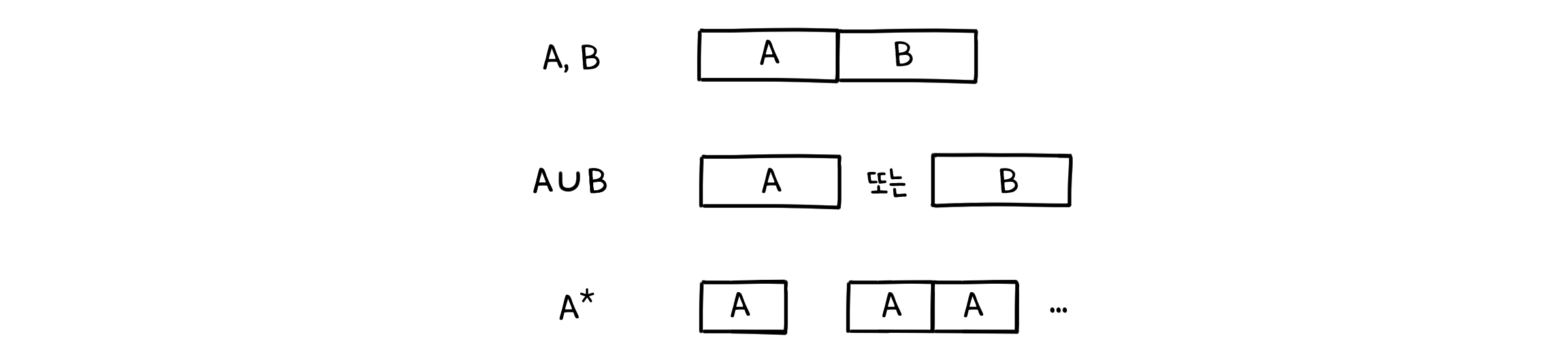
• $A, B$가 정규 표현식이라면, 다음도 정규 표현식에 포함됩니다.

  • $(A, B)$ : $A$와 $B$를 앞 뒤로 합쳐 놓았습니다.

  • $(A \cup B)$ : $A$와 $B$의 합집합입니다.

  • $A^{*}$ : $A$가 하나 이상 반복되거나, 아예 존재하지 않는 빈 문자열 $\lambda$입니다(Kleene closure).

 정규 표현식의 규칙은 단순하게 정의되어 있습니다. 하지만 각각의 연산을 적절하게 조합한다면, 복잡한 규칙이나 의미도 간단하게 나타낼 수 있습니다. 단순하게 0과 1로만 이루어진 언어 체계가 있다고 가정해도, 아래와 같이 다양한 패턴의 언어 체계를 생각해 낼 수 있습니다.

표현식	규칙
10*	1 다음에 0만 따라 붙는 문자열
(10)*	10이 반복되는 문자열
0 $\cup$ 01	0 또는 01
0(0 $\cup$ 1)*	0으로 시작하는 문자열
(0*1)*	0으로 끝나지 않는 문자열

 우리는 맨 처음에 이전 장의 FSA 예시 하나를 들어 보며 시작했습니다. 그리고 짐작하는 것 처럼, 정규 표현식의 규칙은 FSA의 형태로 나타낼 수 있습니다. 다소 직관적인 사실이긴 하지만, 1956년 미국의 수학자 스티븐 콜 클리니(Stephen Cole Kleene)는 이를 직접 증명하며 공식적인 정리로 남기게 되었습니다.

Theorem 1. 클리니의 정리 (Kleene’s Theorem)
정규 표현식의 집합은 FSA로도 정의할 수 있다. 그 반대도 성립한다.

 이 정리가 가지는 의미는 상당히 중요합니다. 왜냐하면, 보는 것 처럼 정규 표현식은 조합이 길어질 수록 보기가 불편하거든요. 하지만 우리는 정규 표현식과 FSA가 같은 언어 계층을 정의할 수 있다는 사실을 알게 되었으니, 복잡한 언어 체계를 정의할 때 정규 표현식 대신 FSA를 사용해도 된다는 결론에 다다를 수 있습니다.

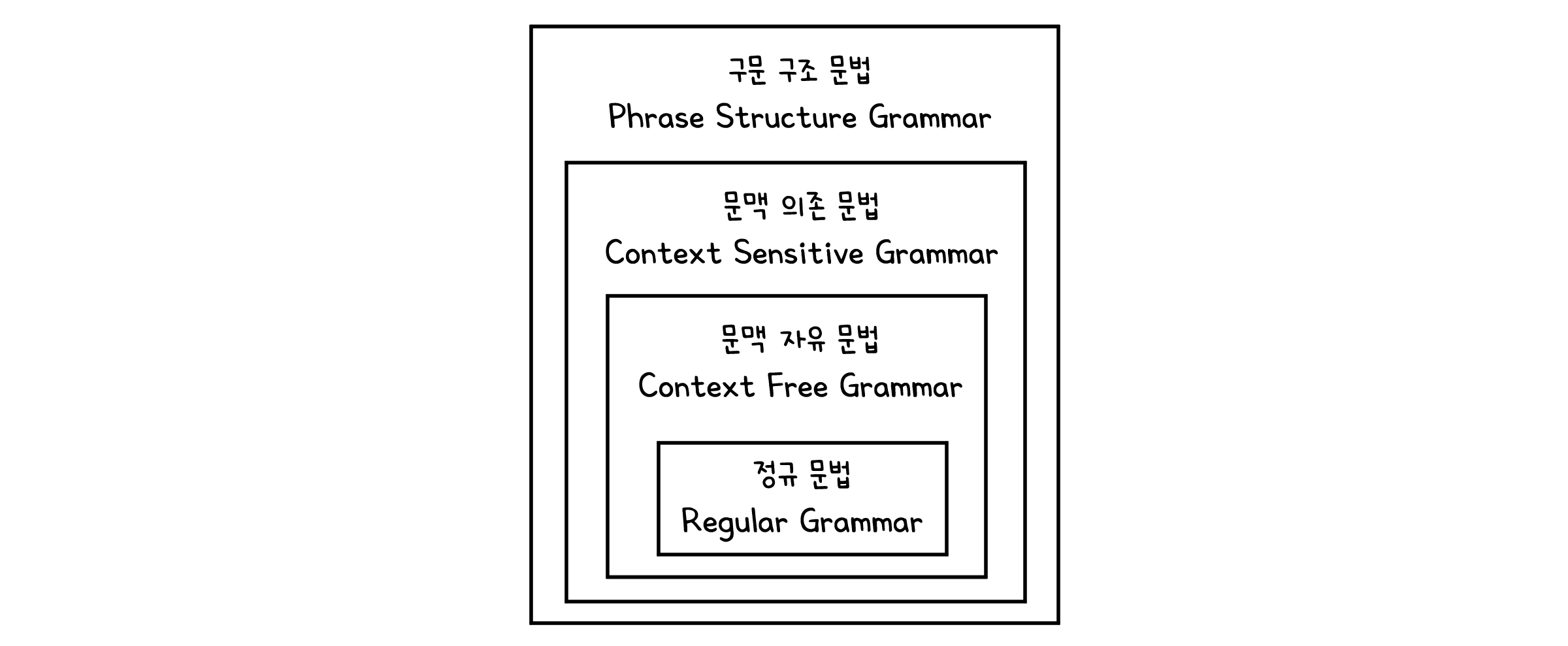
문법의 분류

 구문 구조 문법은 어떠한 형태의 생성규칙이라도 모두 허용되는, 가장 넓은 의미의 문법 체계입니다. 여기에 조건을 추가하여 좀 더 특수한 형태의 문법 체계를 정의할 수 있는데, 미국의 언어학자 에이브럼 놈 촘스키(Avram Noam Chomsky)는 조건에 따라 크게 세 가지 단계의 문법 위계를 제시하였습니다.

문맥 의존 문법 (Context Sensitive Grammar, CSG)

 문맥 의존 문법(Context Sensitive Grammar, CSG)은 구문 구조 문법 다음으로 넓은 의미를 가지는 문법 체계입니다. 비단말 기호가 어떤 문맥 사이에서 나타나는지에 따라 그 규칙이 달라질 수 있습니다. $\alpha, \beta, w \in V^{*}$라고 할 때, 이를 생성규칙 표기로 나타내면 아래와 같습니다.

\[\alpha A \beta \; \rightarrow \; \alpha w \beta\] \[S \rightarrow \lambda\]

 CSG의 대표적인 예시는 ${ a^nb^nc^n }$입니다. a, b, c가 각각 n번씩 연달아 있다는 뜻입니다. 이는 아래와 같은 생성 규칙으로 만들어낼 수 있습니다.

\[S \rightarrow aSBC\] \[S \rightarrow aBC\] \[CB \rightarrow BC\] \[B \rightarrow b\] \[C \rightarrow c\]

 \(CB \rightarrow BC\)가 핵심적인 규칙인데, 문맥을 보며 그 순서를 바꾸는 부분이기 때문입니다. 아래에서 소개할 문맥 자유 문법에서는 이러한 생성 규칙을 정의할 수 없습니다.

\(CB \rightarrow BC\)는 처음에 제시한 CSG의 생성규칙과는 정확히 맞아 떨어지지 않습니다. 이는 \(\alpha A \beta \; \rightarrow \; \alpha w \beta\)의 형태가 CSG의 특별한 경우 중 하나이기 때문입니다. 더 넓은 정의를 사용한다면 \(CB \rightarrow BC\)는 충분히 CSG의 생성규칙에 포함될 수 있습니다.

문맥 자유 문법 (Context Free Grammar, CFG)

 문맥 자유 문법(Context Free Grammar, CFG)은 문맥에 관계 없이 비단말 기호를 바꿀 수 있는 문법 체계입니다. 문맥 의존 문법에서 양 옆의 문맥이 모두 빈 문자열인 경우라고 생각할 수 있습니다. $w \in V^{*}$라고 할 때, 이를 생성규칙 표기로 나타내면 아래와 같습니다.

\[A \rightarrow w\]

 CFG의 대표적인 예시는 ${ a^nb^n }$입니다. 이에 대한 규칙은 간단하게 나타낼 수 있습니다.

\[S \rightarrow aSb\] \[S \rightarrow ab\]

정규 문법 (Regular grammar)

 정규 문법(Regular grammar)은 가장 좁은 의미의 문법 체계입니다. 말 그대로 정규 표현식에 대한 문법이라고 할 수 있습니다. 위에서 정의했던 정규 표현식에 대한 규칙을 $G=(V, T, S, P)$의 형태로 나타낸 것이죠. 정규 문법의 생성 규칙($P$)은 문자열을 확장하는 방향에 따라 좌측 정규 문법(right regular grammar)과 우측 정규 문법(left regular grammar) 두 가지로 나뉩니다.

요소	예시
좌측 정규 문법	$S \rightarrow aS$ $S \rightarrow bA$ $A \rightarrow \lambda$ $A \rightarrow cA$
우측 정규 문법	$S \rightarrow Sa$ $S \rightarrow Ab$ $A \rightarrow \lambda$ $A \rightarrow Ac$

 클리니의 정리에 의해 우리는 이 문법 체계를 FSA의 형태로 나타낼 수 있습니다. 나타내는 방법은 여러가지가 있겠지만, 여기서는 아래와 같이 표현하였습니다. 물론, 이 FSA를 통해서 정규 문법의 규칙을 유추할 수도 있겠죠.

 촘스키가 고안한 문법 위계는 그 단계가 올라갈 수록 조건이 더해져 표현할 수 있는 범위가 제한됩니다. 하지만 이 말은 곧 이전 단계의 문법 체계로 다음 단계의 문법 체계를 나타낼 수 있다는 뜻이죠. 정규 문법은 문맥 자유 문법만으로도 나타낼 수 있으며, 문맥 자유 문법은 문맥 의존 문법만으로도 나타낼 수 있습니다. 따라서 이들은 연속적인 포함관계를 가지게 됩니다.

배커스-나우르 표기법 (Backus-Naur Form)

 배커스-나우르 표기법(Backus-Naur Form)은 문맥 자유 문법을 명확히 정의하기 위해 고안된 표기법입니다. 배커스-나우르 표기법은 아래 규칙들을 따릅니다.

• 좌변에는 하나의 비단말 기호만이 존재한다.

• 비단말 기호는 브라켓(<>)으로 감싸 표기한다.

• 생성규칙의 화살표(→)는 ::=으로 표기한다.

• 같은 비단말 기호에서 생성되는 규칙은 or 연산자(|)로 묶어 표기한다.

 예를 들어 $A \rightarrow Aa, A \rightarrow a, A \rightarrow AB$를 생성규칙으로 가지는 문법을 배커스-나우르 표기법으로 나타내면 이렇게 됩니다.

\[<A>\;::=\;<A>a\;|\;a\;|\;<A><B>\]

튜링 머신 (Turing Machine)

 앞서 우리는 클리니의 정리에 따라 정규 문법을 FSA로 바꾸어 나타내 보았습니다. 이는 정규 문법에 있어서 중요한 특징이었습니다. 하지만 정규 문법 위에는 더 넓은 의미의 문법 체계들이 있었습니다. 이들은 항상 FSA로 나타내지 못할테고요. 그렇다면, FSA 말고도 넓은 의미의 문법 체계들에 사용할 수 있는 계산 모델은 없는 걸까요?

 이에 대한 해답을 제시하는 것이 바로 튜링 머신(Turing Machine)입니다. 튜링 머신은 무한한 테이프와 유한한 제어 장치를 이용해 계산 가능한 모든 절차를 모델링할 수 있는 계산 모델이라고 정의됩니다.

 튜링 머신의 구조를 뜯어보면서 이게 당최 무슨 말인지 알아보도록 합시다.

튜링 머신의 구성요소

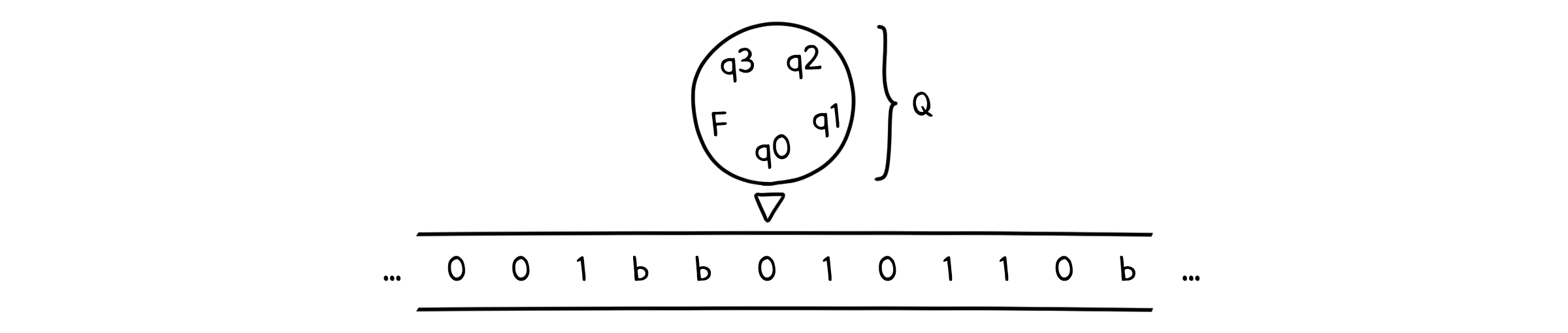
 다섯 가지 요소($S, I, O, f, g, S_0, F$)로 이루어진 FSA와 달리, 튜링 머신은 무려 일곱 가지의 요소를 가집니다.

• 상태(state)의 집합 $Q$

• 테이프 알파벳(tape alphabet)의 집합 $\Gamma$

• 공백 기호 $b \in \Gamma$

• 입력 알파벳(input alphabet) $\Sigma \subseteq \Gamma - { b }$

• 초기 상태 $q_0 \in Q$

• 최종 상태 $F \subseteq Q$

• 전이 함수 $\delta : (Q - F) \times \Gamma \rightarrow Q \times \Gamma \times { L, R }$

 위의 값들로 정의되는 튜링 머신 $M$은 아래와 같이 표기할 수 있습니다.

\[M = (Q, \Gamma, b, \Sigma, \delta, q_0, F)\]

동작 방식

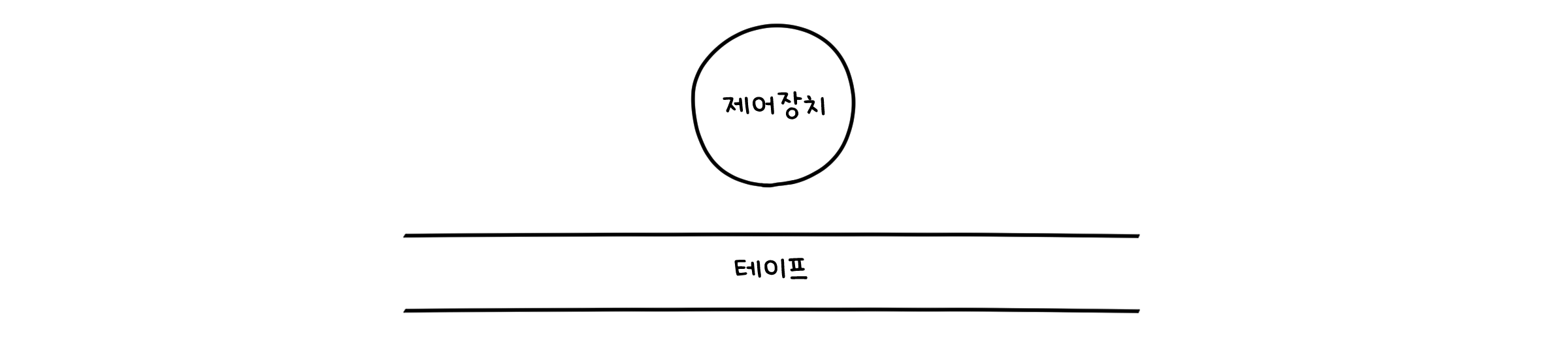
 아직까지는 전혀 감이 잡히지 않습니다. 계속해서 언급되는 테이프가 대체 무엇일까요? 튜링 머신은 크게 상태를 관리하는 제어 장치(Control Unit)와 입력값을 관리하는 테이프(Tape) 두 부분으로 나뉘어집니다.

 테이프의 각 부분에는 입력 알파벳($\in \Sigma$)이 표기되어 있습니다. 제어장치는 테이프에 표기된 알파벳 중 한 부분에 위치해 있으며, 초기상태 $q_0$를 가지고 시작합니다. 맨 처음 말 했던 것 처럼 제어장치는 유한하며, 테이프는 무한히 펼쳐져 있습니다. 이는 상태의 수는 유한하며, 입력값은 끝없이 들어갈 수 있다는 것을 의미합니다.

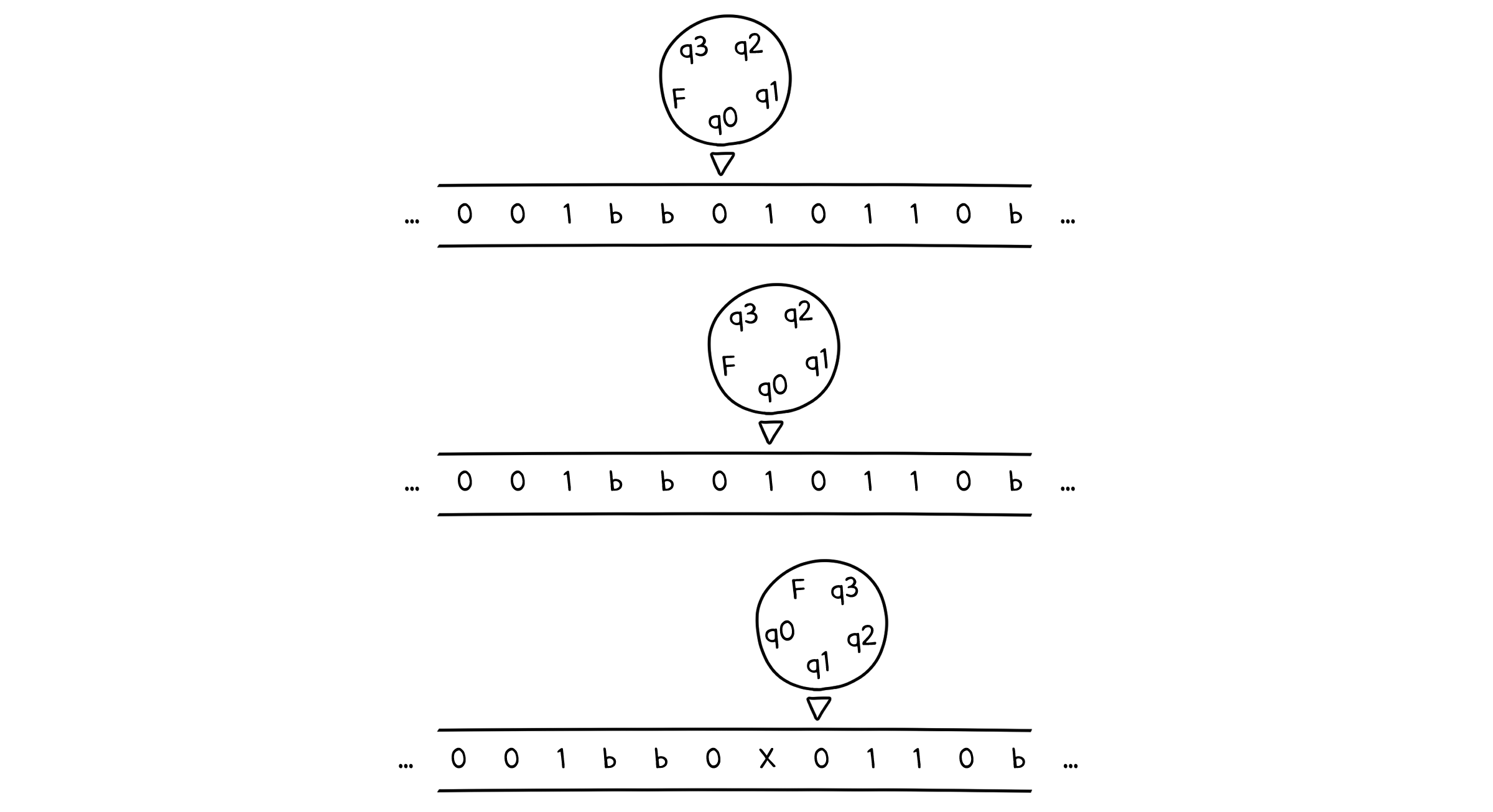
 이제 제어장치가 테이프에 적혀진 알파벳을 하나씩 읽을 것입니다. 그리고 현재 상태($(Q - F)$)와 읽은 기호($\Gamma$)에 따라 1. 상태를 바꾸거나($Q$) 2. 새로운 알파벳을 쓰거나($\Gamma$) 3. 제어장치를 왼쪽 또는 오른쪽으로 이동할 수 있습니다(${ L, R }$). 이 때 새로운 알파벳은 입력 알파벳에 속하지 않은 테이프 알파벳($\Gamma - \Sigma$)을 사용할 수도 있습니다.

 그리고 마지막에 최종상태에 도달한다면 튜링머신은 종료되는 것이죠.

튜링 머신 - 예시

 좀 더 쉽게 와닿을 수 있도록, 이전에 CSG 언어의 예시로 들었던 ${ a^nb^nc^n }$ 로 튜링 머신을 만들어봅시다. 기본적으로 이렇게 설계할 거에요.

• 입력값의 끝부분 부터는 공백(⊔)만이 무한히 이어진다.

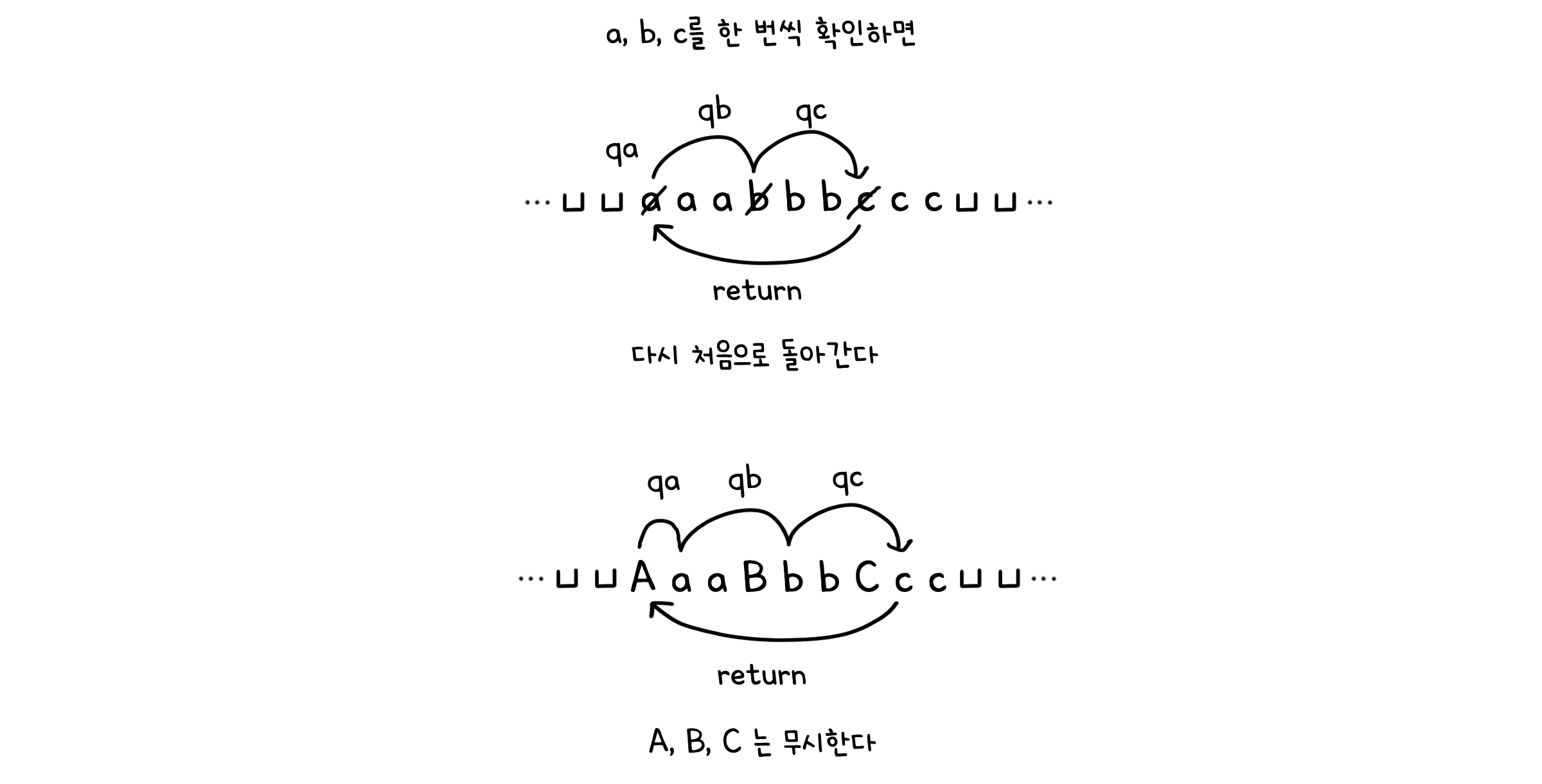
• a, b, c를 한 번씩 번갈아가며 존재 여부를 체크한다.

• a 까지 체크했을 때 b가 없거나, b 까지 체크했을 때 c가 없다면 종료한다.

• 존재가 확인된 알파벳은 대문자로 치환한다. 즉 A, B, C는 이미 확인된 a, b, c로 취급한다.

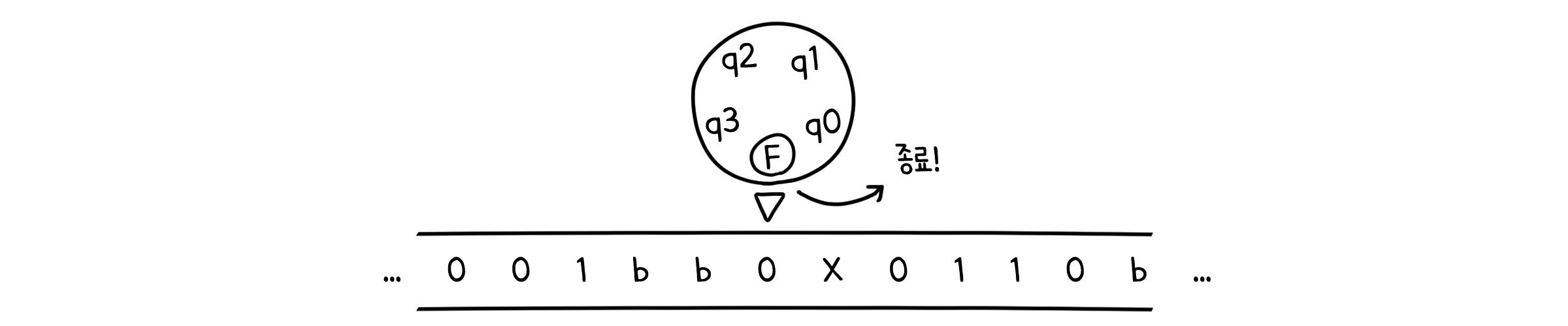
• 한 번 a, b, c를 모두 체크했으면, 다시 맨 앞 부분으로 돌아와 새로운 루프를 시작한다. 이 때 A, B, C는 무시한다.

• 다음 루프에서 a가 모두 A로 치환되었다면, b와 c의 존재 여부를 체크한다. 존재하지 않으면 최종상태로 전이하고, 존재한다면 종료한다.

 이를 위해 필요한 상태는 각 기호를 탐색 하는 상태 (qa, qb, qc), 처음으로 다시 복귀하는 상태 (return), 그리고 더 이상 a가 없을 때 잔여 기호가 남았는지 확인하는 상태 (final)가 필요할 것입니다. a가 맨 처음에 와야 하기 때문에, 초기 상태는 qa가 되어야 할 것입니다. 수용 상태는 accept, 종료는 reject로 정의합니다.

\[Q = \{ qa, qb, qc, return, final, accept, reject \}\]

 필요한 기호는 입력값인 a, b, c 세 가지에 더해 이미 체크를 완료한 기호인 A, B, C 세 가지가 추가로 필요할 것입니다. ⊔는 어떠한 값도 들어 있지 않은 공백입니다.

\[\Gamma = \{ a, b, c, A, B, C, ⊔ \}\]

 맨 위에서 설계한 규칙은 아래와 같은 전이 함수로 나타낼 수 있습니다. $Q \times \Gamma$의 범위가 커 복잡해 보이지만, 천천히 살펴보면 이해할 수 있을 거에요.

	a	b	c	A	B	C	⊔
qa	qb, A, R	final, b, R	final, c, R	qa, A, R	qa, B, R	qc, C, R	final, ⊔, R
qb	qb, a, R	qc, B, R	reject, c, R	qb, A, R	qb, B, R	reject, ⊔, R	reject, ⊔, R
qc	reject, a, R	qc, b, R	return, C, L	qc, A, R	qc, B, R	qc, C, R	reject, ⊔, R
return	return, a, L	return, b, L	return, c, L	return, A, L	return, B, L	return, C, L	qa, ⊔, R
final	reject, a, R	reject, b, R	reject, c, R	final, A, R	final, B, R	final, C, R	accept, ⊔, R

새로운 시작을 위하여

 직관적으로 계산 가능한 모든 문제는 어떻게든 튜링머신으로도 계산할 수 있습니다. 하지만 튜링머신도 한계가 있습니다. ‘주어진 문제가 과연 끝낼 수 있는 문제인가?’에 대한 답, 즉 정지문제에 대해서는 명쾌한 해법을 제시하지 못합니다. 그렇다면 튜링머신을 웃도는 상위의 계산모델로 해결해야 하는 걸까요?

 1936년, 앨런 튜링은 정지 문제를 해결하는 알고리즘이 존재하지 않는다는 사실을 증명하였습니다.

 이로써 사람들은 그 전까지 가지고 있던 수학 체계의 완전무결정에 대한 믿음을 깨뜨려버렸습니다. 하지만 이는 전혀 절망적인 사실이 아닙니다. 오히려 우리가 무엇을 할 수 있고, 무엇에 집중해야 하는지를 새로이 알려주게 되었죠. 계산이 가능한가? 보다 현실적인 시간 안에 계산이 가능한가?에 주목하게 되었고, 양자 컴퓨팅이나 인공지능을 사용해서 현실적인 시간의 장벽을 낮추려 하는 시도도 생겨났습니다.

 이렇듯 우리가 주어진 자리에서 끝없이 새로운 방법을 찾고 있습니다. 어쩌면 그것이 복잡한 이산 수학 세계를 바라보는 새로운 방향성을 줄 수 있지 않을까요?