[CM201] 10. 유한 상태 오토마타 (FSA)

 자판기가 망가졌네요.

 그렇다면 직접 자판기를 만들어봅시다! 망가진 자판기는 사과주스 하나만 파는 간단한 형태라고 생각합시다. 자판기는 명확한 입력값(금액)과 출력값(음료)를 가지고 있으니, 이런 식으로 만들어지게 될 것입니다.

 추가로 사과 주스 하나는 500원, 한 번에 하나씩만 뽑을 수 있으며 500원이 넘는 금액을 넣으면 차액만큼 거스름돈을 반환해준다고 합시다. 조금 복잡해지겠지만, 조건문과 분기를 사용한다면 어렵지 않게 나타낼 수 있겠죠.

 이제 자판기가 잘 돌아가는지 시험해볼까요. 500원을 넣어보면…

 완벽합니다! 한 번 더 뽑아볼까요.

 500원이 없으면, 100원을 다섯 개 넣어보죠.

 저런, 문제가 생겼네요. 자판기가 동전을 먹어버렸나봅니다. 우리가 만든 자판기는 들어온 금액이 500원을 넘는지만 판단할 뿐, 남은 금액이 얼마인지는 기억하지 못합니다. 그래서 500원 보다 적은 돈이 들어오면 그냥 증발할 뿐이죠.

 아무리 100원을 계속 넣어도 자판기는 알지 못합니다. 이 문제를 해결하려면, 자판기는 자신이 얼마를 가지고 있는지 기억할 필요가 있습니다.

유한 상태 기계 (Finite State Machine, FSM)

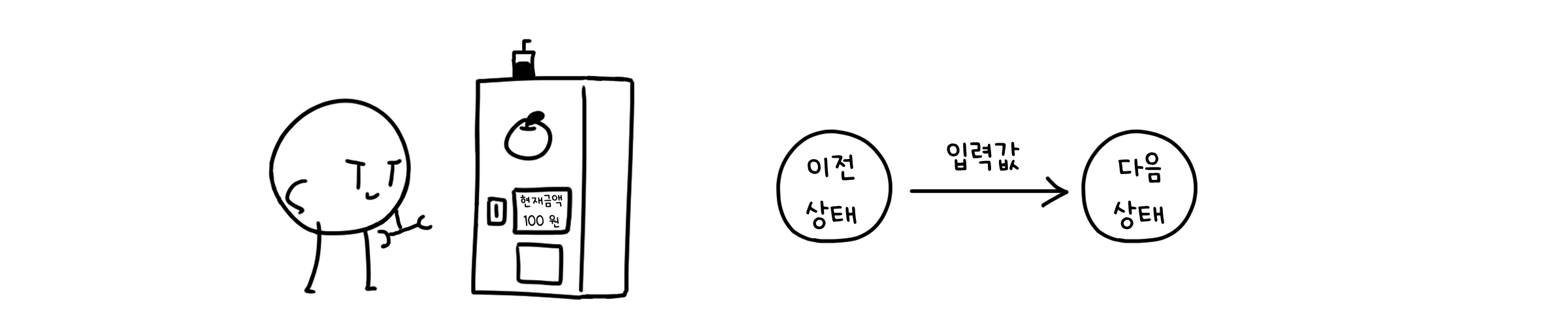
 직전에 어떤 입력값이 있었는지, 즉 이전 상태(state)를 기억할 수 있도록 해야 합니다. 자판기가 가지고 있는 금액 양을 상태값이라고 정의한다면, 자판기는 500원 보다 적은 금액을 받아도 자신이 얼마를 받았는지 그 상태를 기억할 수 있을 것입니다. 억울하게 동전이 먹힐 일도 없겠죠.

 유한 개의 상태를 가지고, 입력값에 따라 현재 상태를 바꾸며 동작하는 계산 모델(혹은 시스템)을 유한 상태 기계(Finite State Machine, FSM)라고 합니다. 상태값을 사용한다면, 같은 입력값을 받더라도 직전에 어떤 상태였는지에 따라 다른 동작을 이끌어 낼 수 있습니다.

FSM의 구성 요소

 FSM은 기본적으로 아래 여섯 가지 요소들로 이루어집니다.

• 상태(state)의 집합 $S$

• 입력값(input)의 집합 $I$

• 출력값(output)의 집합 $O$

• 상태가 전이되는 함수 $f : \; S \times I \rightarrow S$

• 출력값을 내놓는 함수 $g : \; S \times I \rightarrow O$

• 초기 상태 $S_0$

 위의 값들로 정의되는 유한 상태 기계 $M$은 아래와 같이 표기할 수 있습니다.

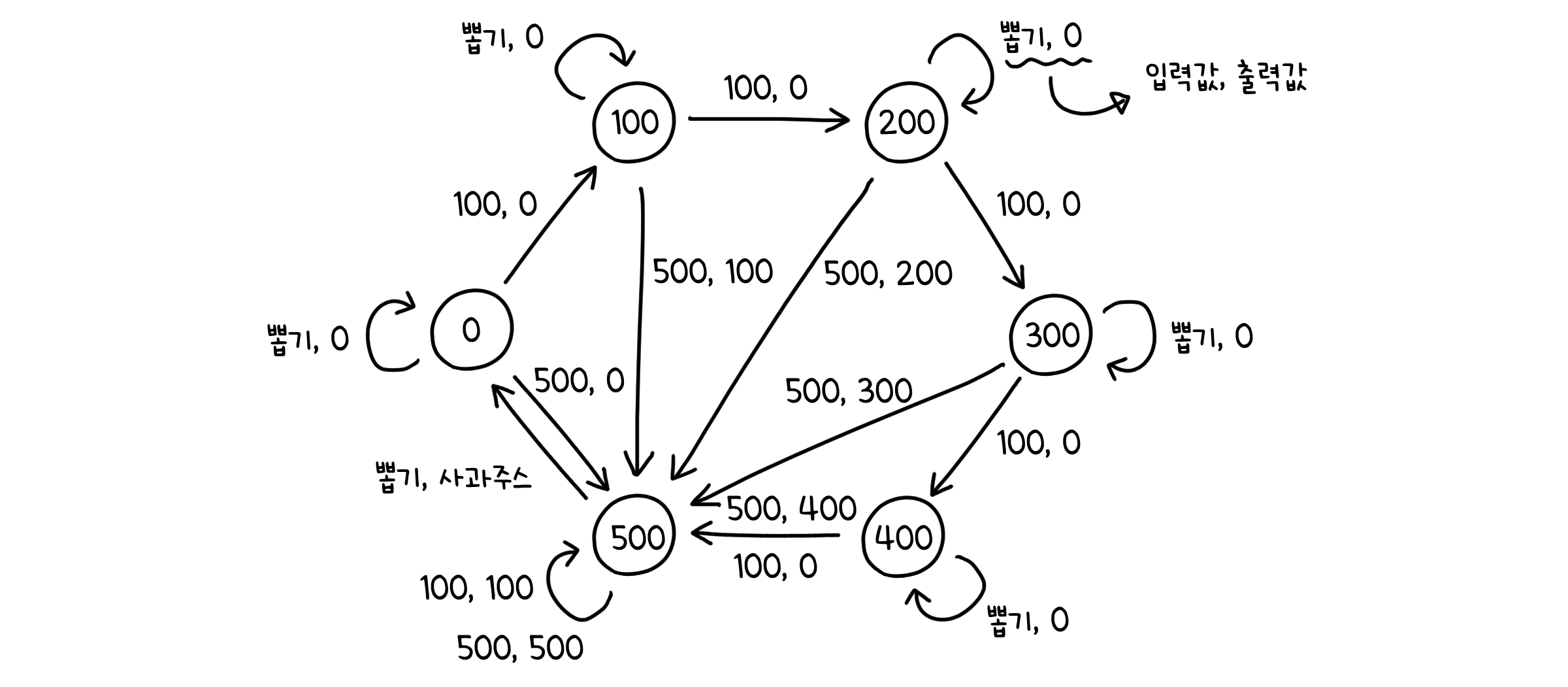
\[M = (S, I, O, f, g, S_0)\]

 우리의 자판기에 상태를 도입해서 FSM으로 만들어봅시다. 이전에 말했듯 가지고 있는 금액 양을 상태로 둔다면, 이렇게 생각할 수 있겠습니다.

• 초기 상태(원) : 0

• 상태(원) : { 0, 100, 200, 300, 400, 500 }

• 입력값 : { 100, 500, 뽑기 }

• 출력값 : { 0, 100, 200, 300, 400, 500, 사과주스 }

• 전이 함수 :
  • 입력값을 상태에 더함.
  • 상태가 500원을 넘게 되면, 상태는 500원으로 유지.
  • 뽑기 시행시, 상태가 500원이라면 0원으로 전이. 그 외에는 전이 없음.
• 출력 함수 :
  • 상태가 500원을 넘게 되면, 차액 만큼 출력
  • 뽑기 시행시, 상태가 500원이라면 사과주스 출력
  • 그 외에는 모두 0원 출력

 이제 500원이 없어도 사과주스를 뽑아 먹을 수 있겠네요!

유한 상태 오토마타 (Finite State Automata, FSA)

 당신은 당신의 친구과 맛있는 사과주스를 나눠 마시기로 합니다. 금액은 신경 쓰지 말고, 얼마나 뽑을지 생각해보자고요.

 아무래도 둘이 공평하게 나눠 먹으려면, 수가 짝수 개가 되도록 뽑아야 하겠죠. 공평한건 중요하니까, 짝수 개 만큼 음료를 뽑지 않으면 음료를 내어 주지 않도록 자판기를 손 보도록 합시다.

 이 시스템은 거스름돈을 반환하거나 음료를 내보내는 것이 아닌 적절한 주문을 했는지 판단하는 것이기 때문에, 별도의 출력값이 필요하지 않습니다. 다만, 어떤 상태가 적합한 상태인지 정의할 필요가 있죠. 뽑기로 한 사과 주스의 개수를 홀수와 짝수 두 가지의 상태로 나누어 봅시다. 그러면 상태값이 짝수가 되었을 때 적합하다고 할 수 있을 것입니다.

• 초기 상태 : 짝
• 상태 : { 짝, 홀 }
• 입력값 : { 뽑기 }
• 전이 함수 :
  • 짝에서 뽑기를 시행하면 홀로 전이한다.
  • 홀에서 뽑기를 시행하면 짝으로 전이한다.
• 적합한 상태 : { 짝 }

 이렇게 우리는 또 하나의 상태 기계를 만들었는데, 이전과는 달리 출력값이 없는데다 상태의 적합 여부도 판단할 수 있게 되었습니다. 이를 유한 상태 오토마타(Finite State Automata, FSA)라고 합니다. 적합하다고 판단되는 상태는 수용 상태(Accepting state) 또는 최종 상태(Final state)라고 하고요. 따라서 FSM은 최종 상태 $F$가 추가되었을 때 아래와 같이 정의할 수 있습니다.

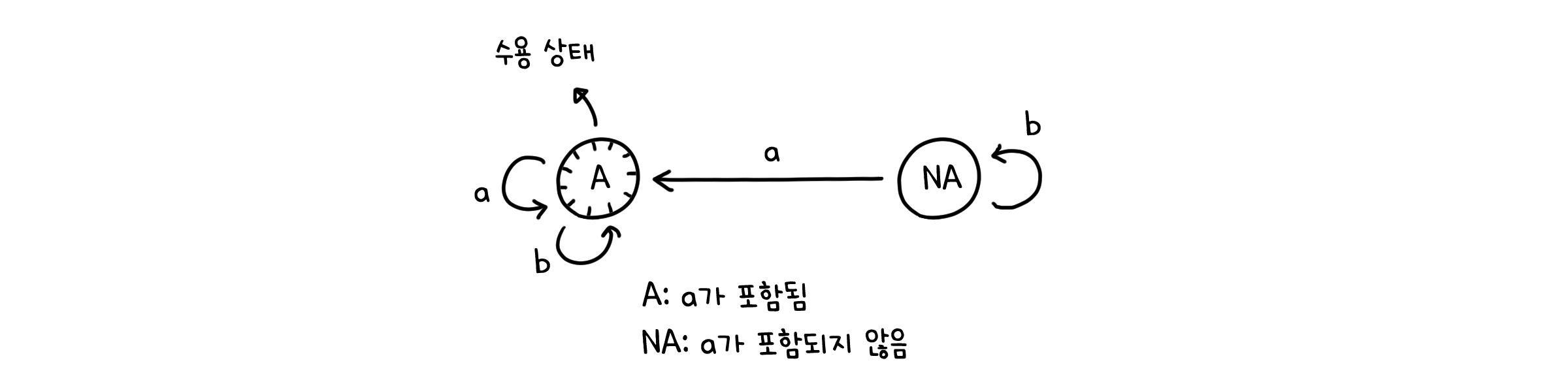
\[M = (S, I, f, S_0, F)\]

 FSM과 FSA는 출력값과 수용 상태의 유무를 제외하면 거의 똑같은 방식으로 작동하지만, 그 사용처는 조금 다릅니다. FSM은 어떻게 행동하느냐에 중점이 맞추어져 있다면, FSA는 어떤 것을 허락하느냐에 중점이 맞추어져 있다고 볼 수 있죠. 또 하나의 예를 들어봅시다. 만약 a와 b만으로 이루어진 문자열이 있다고 했을 때, 그 문자열에 a가 포함되는지 판단한다고 합시다. 문자열의 순서대로 문자를 입력한다고 하면, 이런 형태의 FSA를 만들 수 있습니다.

 실제로 어떤 출력값을 내놓지는 않지만, 입력이 끝난 시점의 상태를 통해 해당 문자열이 올바른 입력인지(=a를 포함하는지)를 판단할 수 있습니다. 따라서 FSA의 모양과 관계 없이 같은 수용 상태에 대해 똑같은 입력값을 가진다면, 그 FSA들은 동치(Equivalent)인 것으로 간주합니다.

비결정적 유한 상태 오토마타 (Nondeterministic FSA, NFSA)

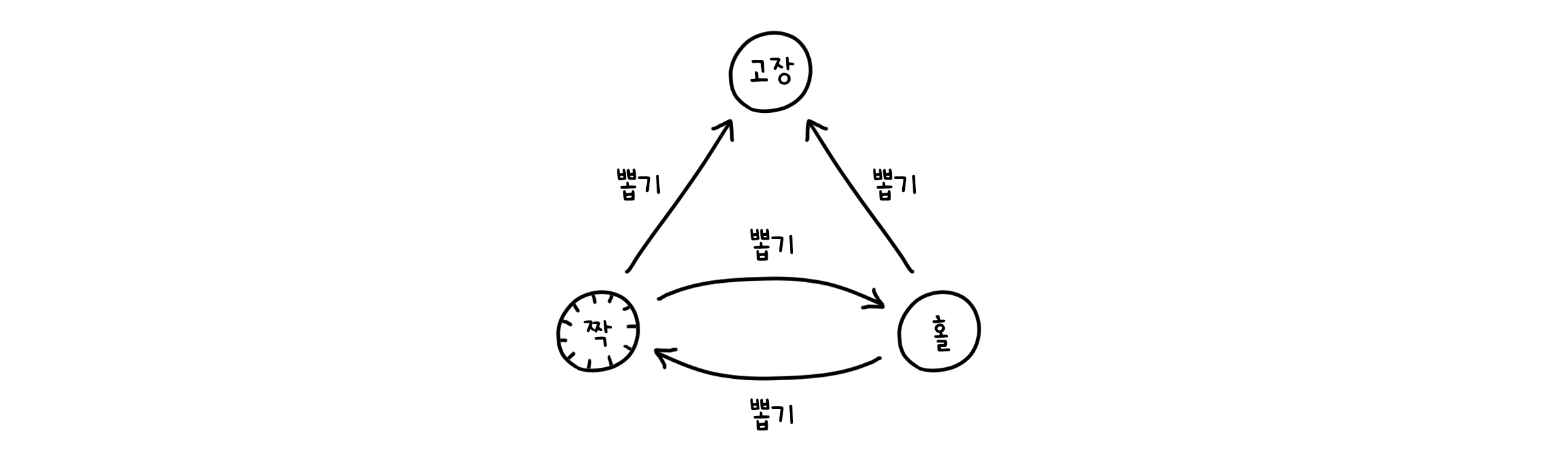
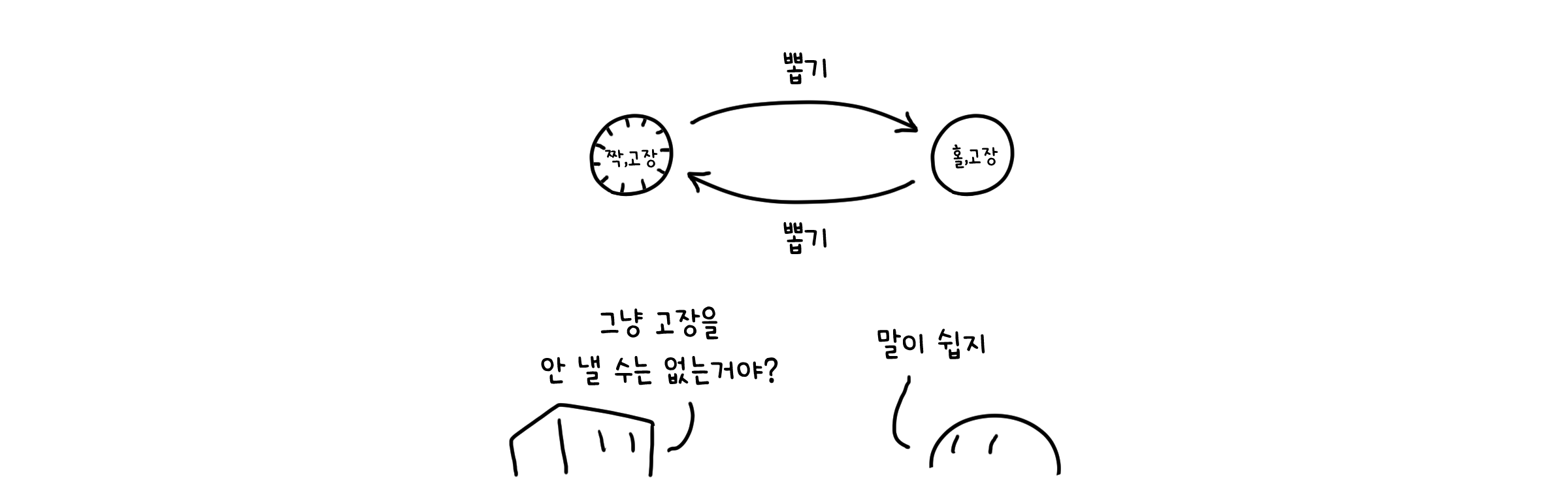
 우리는 앞서 자판기가 훌륭하게 작동하는 것을 확인했습니다. 하지만 현실세계의 기계장치라면, 결함과 오작동이 발생하는 것이 필연적이죠. 자판기가 고장나는 때도 있을 것입니다. 그러면 어떻게 해야 할까요? 우선 자판기를 고치기 전에 누군가 섣불리 사용하지 못하게 막아야 하겠죠. 고장난 기계를 막 다루는 건 썩 유쾌하지 않은 결과를 초래할 수 있습니다.

 기계에 새로운 상태 ‘고장’을 추가해봅시다. 우리가 어떤 동작을 하던, 일정 확률로 자판기는 고장날 것입니다. 그리고 ‘고장’ 상태가 되면, 사용자가 상호작용할 수 없도록 어떠한 동작도 부여하지 않습니다.

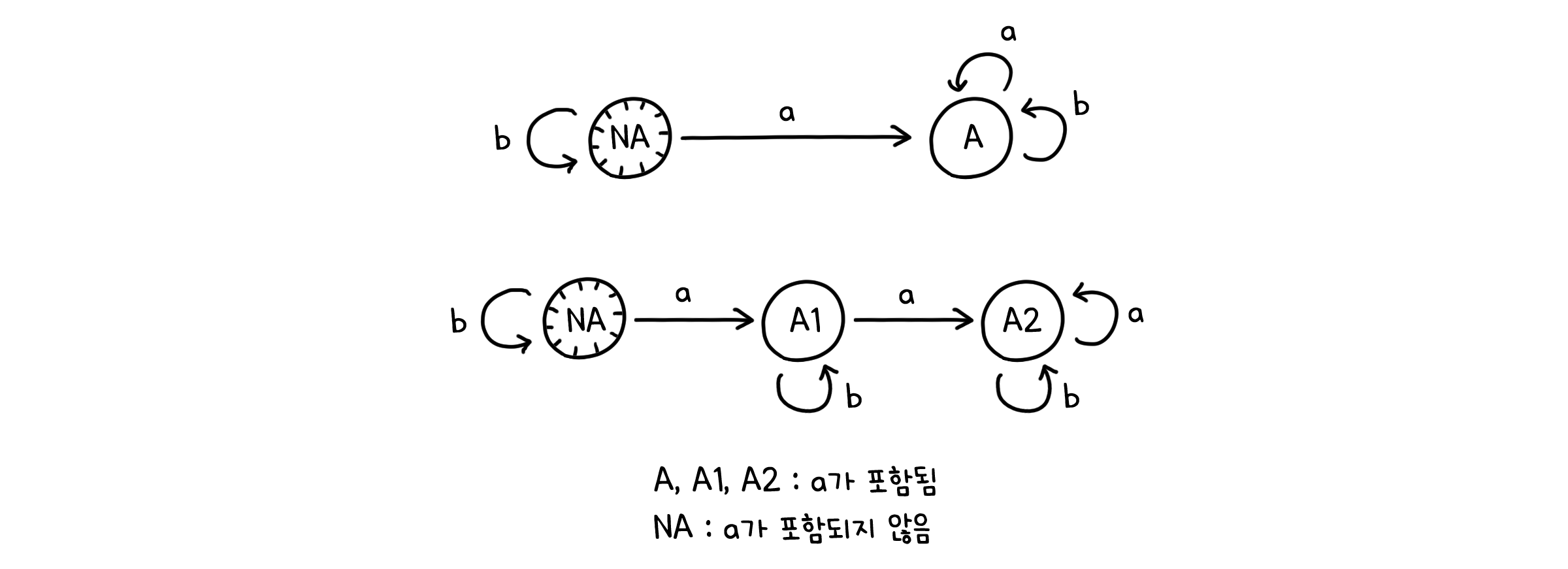
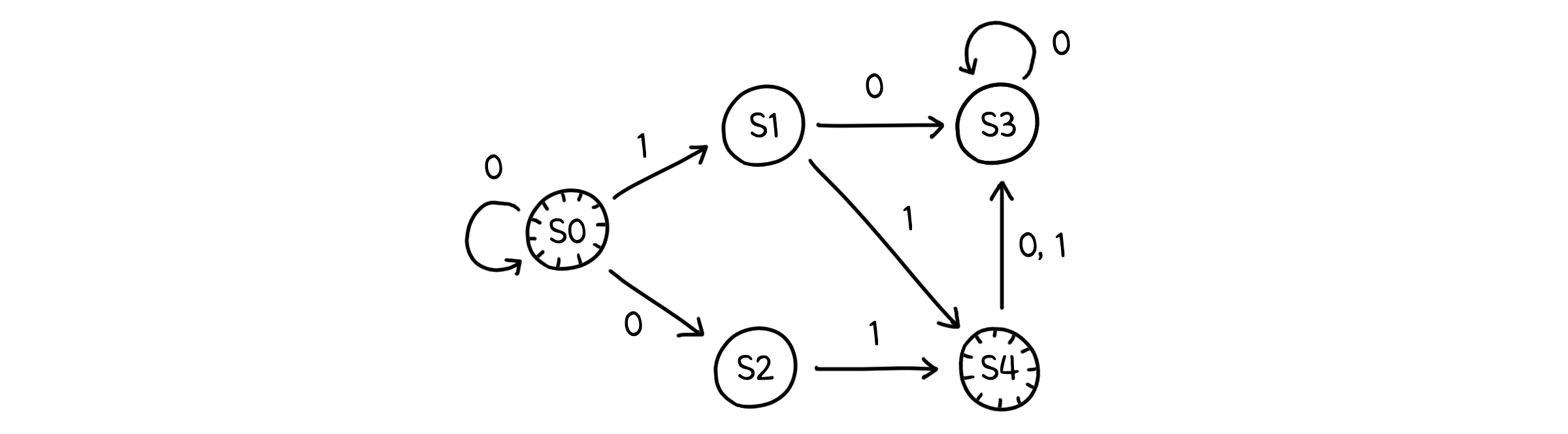
 모든 상태가 어떤 입력값에 대해 다른 상태로 이동하는 전이동작(Transition)이 있다면, 그것을 결정적 유한 상태 오토마타(Deterministic FSA, DFSA)라고 합니다. 이때까지 우리가 다룬 예시들은 모두 여기에 속해 있었어요. 하지만 위와 같은 경우 처럼 1.같은 입력값에 대해 여러 전이가 있거나 2.어떤 전이도 존재하지 않는 상태가 있다면, 그것은 비결정적 유한 상태 오토마타 (Nondeterministic FSA, NFSA)라고 합니다.

 모든 NFSA는 DFSA의 형태로 바꿀 수 있습니다. 즉 동시에 여러 상태로 전이하는 비결정성은 단지 편의를 위한 표현일 뿐, 얼마든지 결정적인 형태로도 나타낼 수 있는 것입니다. 다만 이 때 DFSA의 상태는 NFSA에서 ‘다음 단계에 전이 가능한 모든 상태’의 집합으로 표현해야 합니다. 말로만 설명하면 어려우니, 간단한 예를 들어보겠습니다.

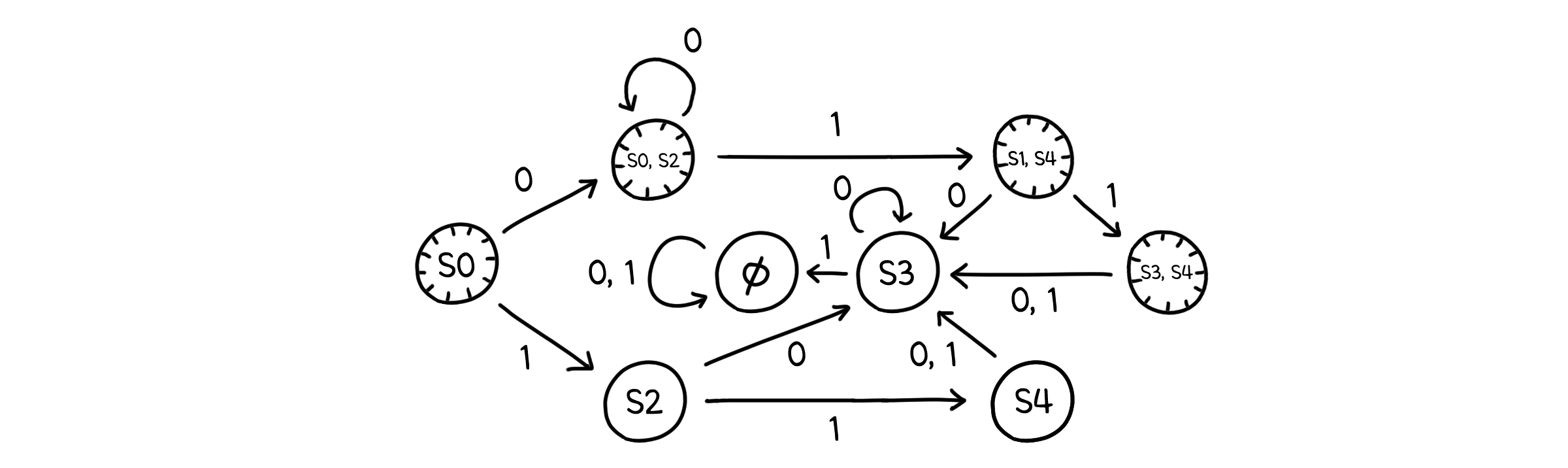
 위 NFSA는 시작 상태 S0에서 0을 입력값으로 받았을 때 두 가지 전이를 가집니다(S0과 S2). DFSA는 한 입력값에 하나의 전이를 가져야 하니, S0에서 0을 입력값으로 받을 때 전이되는 상태는 두 가지 전이를 모두 합쳐 {S0, S2}로 나타냅니다. 그 다음 전이는 또 S0과 S2에서의 전이를 합친 형태로 나타내고, 끝으로 모든 입력값(0, 1)에 대해서 전이가 일어나지 않으면 비어 있는 상태($\emptyset$)로 전이하게 됩니다.

 그러니까, 우리 자판기의 NFSA를 DFSA로 다시 쓰면 이렇게 나타낼 수 있지 않을까요?